CTR學習筆記&程式碼實現3-深度ctr模型 FNN->PNN->DeepFM
這一節我們總結FM三兄弟FNN/PNN/DeepFM,由遠及近,從最初把FM得到的隱向量和權重作為神經網路輸入的FNN,到把向量內/外積從預訓練直接遷移到神經網路中的PNN,再到參考wide&Deep框架把人工特徵互動替換成FM的DeepFM,我們終於來到了2017年。。。
FNN
FNN算是把FM和深度學習最早的嘗試之一。可以從兩個角度去理解FNN:從之前Embedding+MLP的角看,FNN使用FM預訓練的隱向量作為第一層可以加快模型收斂。從FM的角度來看,FM侷限於二階特徵互動資訊,想要學到更高階的特徵互動,在FM基礎上疊加全聯接層就是FNN。
模型
先看下FM的公式,FNN提取了以下的\(W,V\)來作為神經網路第一層的輸入
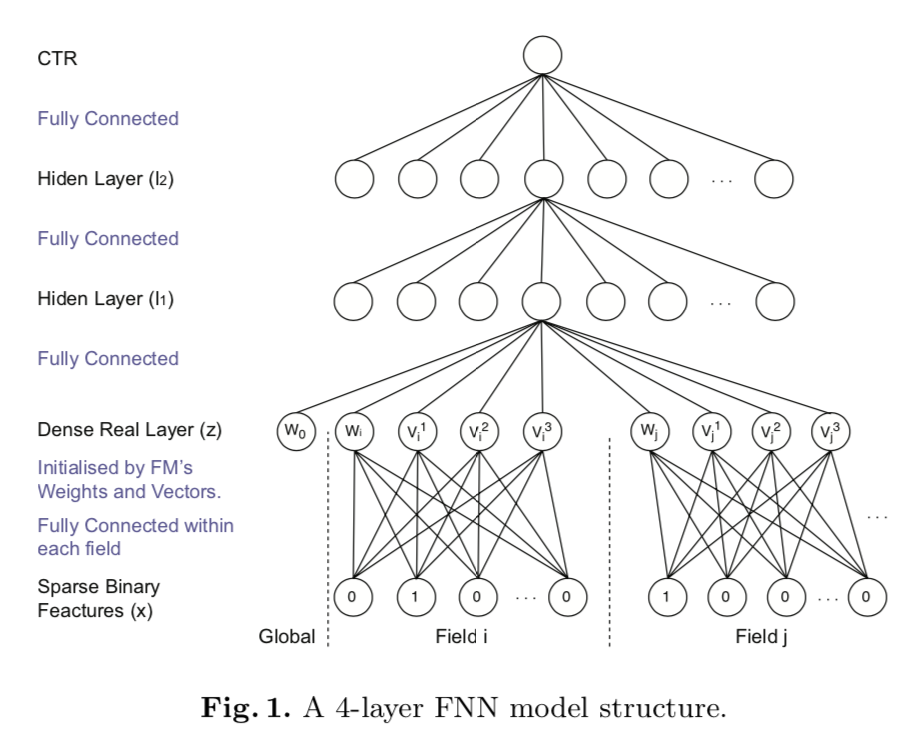
FNN的模型結構比較簡單。輸入特徵N維, FM隱向量維度是K
- 預訓練FM模型提取最終的隱向量\(V = [v_1,v_2,...,v_n] \in R^{N*k} \,\, v_i \in R^{1*K}\)和權重\(w= [w_1,w2,...,w_n] w \in R^{1*N}\)
- FNN模型用\(V\)和\(W\)來初始化神經網路的第一層.模型輸入是由特徵離散化後的one-hot矩陣拼接而成(x),每個離散特徵(i)的one-hot輸入都對映到它的低維embedding上\(z_i = [w_i, v_i] *x[start_i:end_i]\), 第一層是由\([z_1,z_2,...z_n]\)
- 兩個常規的全聯接層到最終給出CTR的預測。
模型結構如下
FNN幾個能想到的問題有
- 非端到端的模型,一點都不優雅有沒有
- 最終FNN的表現會一定程度受到預訓練FM表現的限制,神經網路的最大資訊量<=FM隱向量和權重所含資訊量,當然這不代表FNN會比FM差因為FM對資訊的提取只用了內積
- 從Wide&Deep角度,模型對低階資訊的提煉會比較有限
- 單純的全聯接層對於進一步提煉隱向量上的資訊可能不夠高效
程式碼實現
這裡用了tf.contrib.framework.load_variable去讀了之前FM模型的embedding和weight。感覺也可以直接把FM的variable寫出來,然後FNN裡用params再傳進去也是可以的。
@tf_estimator_model
def model_fn(features, labels, mode, params):
feature_columns= build_features()
input = tf.feature_column.input_layer(features, feature_columns)
with tf.variable_scope('init_fm_embedding'):
# method1: load from checkpoint directly
embeddings = tf.Variable( tf.contrib.framework.load_variable(
'./checkpoint/FM',
'fm_interaction/v'
) )
weight = tf.Variable( tf.contrib.framework.load_variable(
'./checkpoint/FM',
'linear/w'
) )
dense = tf.add(tf.matmul(input, embeddings), tf.matmul(input, weight))
add_layer_summary('input', dense)
with tf.variable_scope( 'Dense' ):
for i, unit in enumerate( params['hidden_units'] ):
dense = tf.layers.dense( dense, units=unit, activation='relu', name='dense{}'.format( i ) )
dense = tf.layers.batch_normalization( dense, center=True, scale=True, trainable=True,
training=(mode == tf.estimator.ModeKeys.TRAIN) )
dense = tf.layers.dropout( dense, rate=params['dropout_rate'],
training=(mode == tf.estimator.ModeKeys.TRAIN) )
add_layer_summary( dense.name, dense )
with tf.variable_scope('output'):
y = tf.layers.dense(dense, units= 1, name = 'output')
tf.summary.histogram(y.name, y)
return y
PNN
PNN的目標在paper最開始就點明瞭以比MLPs更有效的方式來挖掘資訊。在前一篇我們就說過MLP理論上可以提煉任意資訊,但也因為它太過general導致最終模型能學到模式受資料量的限制會非常有限,PNN借鑑了FM的思路來幫助MLP學到更多特徵互動資訊。
模型
PNN給出了三種挖掘特徵互動資訊的方式IPNN採用向量內積,OPNN採用向量外積,concat在一起就是PNN。模型結構如下
- Input層
輸入是N個離散特徵one-hot處理後拼接而成的高維稀疏矩陣,每個特徵對映到相同維度(k)的低維embddding上 - Product層
- Z是線性部分,和‘1’相乘也就是直接把N個K維Embedding拼接得到N*K的稠密矩陣copy過來
- p是特徵互動部分
- IPNN是兩兩特徵做內積\((1*k)*(k*1)\)得到的scaler拼接成p,維度是\(O(N^2)\)
- OPNN是兩兩特徵做外積\((k*1)*(1*k)\)得到\(K^2\)的矩陣拼接成p,維度是\(O(K^2N^2)\)
- PNN就是[IPNN,OPNN]
之後跟全連線層。可以發現去掉全聯接層把權重都設為1,把線性部分對接到最初的離散輸入那IPNN就退化成了FM。

Product層的優化
以上IPNN和OPNN的計算都有維度過高,計算複雜度過高的問題,作者進行了相應的優化。
- OPNN: \(O(N^2K^2) \to O(K^2)\)
原始的OPNN,p中的每個元素都是向量外積的矩陣\(p_{i,j} \in R^{k*k}\),優化後作者對所有K*K矩陣進行了sum_pooling,也等同於先對隱向量求和\(R^{N*K} \to R^{1*K}\)再做外積\(p = \sum_{i=1}^N\sum_{j=1}^N f_if_j^T=f_{\sum}(f_{\sum})^T \, \, f_{\sum}=\sum_{i=1}^Nf_i\) - IPNN: \(O(N^2) \to O(N*K)\)
IPNN的優化又一次用到了FM的思想,內積產生的\(p \in R^{N^2}\)是對稱矩陣,因此在之後全聯接層的權重\(w_p\)也一定是對稱矩陣。所以用矩陣分解來進行降維,假定每個神經元對應的權重\(w_p^n = \theta^n{\theta^n}^T \text{where } \theta^n \in R^N\)
\(w_p^n \odot p = \sum_{i=1}^N\sum_{j=1}^N\theta^n_i\theta^n_j<f_i,f_j>=<\sum_{i=1}^N\delta_i^n,\sum_{i=1}^N\delta_i^n>\)
PNN的幾個可能可以吐槽的地方
- 和FNN一樣對低階特徵的提煉比較有限
- OPNN的部分如果不優化維度太高,在我嘗試的訓練集上基本是沒啥用。優化後這個sum_pooling究竟還保留了什麼資訊,我是沒太琢磨明白
程式碼實現
@tf_estimator_model
def model_fn(features, labels, mode, params):
dense_feature= build_features()
dense = tf.feature_column.input_layer(features, dense_feature) # lz linear concat of embedding
feature_size = len( dense_feature )
embedding_size = dense_feature[0].variable_shape.as_list()[-1]
embedding_matrix = tf.reshape( dense, [-1, feature_size, embedding_size] ) # batch * feature_size *emb_size
with tf.variable_scope('IPNN'):
# use matrix multiplication to perform inner product of embedding
inner_product = tf.matmul(embedding_matrix, tf.transpose(embedding_matrix, perm=[0,2,1])) # batch * feature_size * feature_size
inner_product = tf.reshape(inner_product, [-1, feature_size * feature_size ])# batch * (feature_size * feature_size)
add_layer_summary(inner_product.name, inner_product)
with tf.variable_scope('OPNN'):
outer_collection = []
for i in range(feature_size):
for j in range(i+1, feature_size):
vi = tf.gather(embedding_matrix, indices = i, axis=1, batch_dims=0, name = 'vi') # batch * embedding_size
vj = tf.gather(embedding_matrix, indices = j, axis=1, batch_dims= 0, name='vj') # batch * embedding_size
outer_collection.append(tf.reshape(tf.einsum('ai,aj->aij',vi,vj), [-1, embedding_size * embedding_size])) # batch * (emb * emb)
outer_product = tf.concat(outer_collection, axis=1)
add_layer_summary( outer_product.name, outer_product )
with tf.variable_scope('fc1'):
if params['model_type'] == 'IPNN':
dense = tf.concat([dense, inner_product], axis=1)
elif params['model_type'] == 'OPNN':
dense = tf.concat([dense, outer_product], axis=1)
elif params['model_type'] == 'PNN':
dense = tf.concat([dense, inner_product, outer_product], axis=1)
add_layer_summary( dense.name, dense )
with tf.variable_scope('Dense'):
for i, unit in enumerate( params['hidden_units'] ):
dense = tf.layers.dense( dense, units=unit, activation='relu', name='dense{}'.format( i ) )
dense = tf.layers.batch_normalization( dense, center=True, scale=True, trainable=True,
training=(mode == tf.estimator.ModeKeys.TRAIN) )
dense = tf.layers.dropout( dense, rate=params['dropout_rate'],
training=(mode == tf.estimator.ModeKeys.TRAIN) )
add_layer_summary( dense.name, dense)
with tf.variable_scope('output'):
y = tf.layers.dense(dense, units=1, name = 'output')
add_layer_summary( 'output', y )
return y
DeepFM
DeepFM是對Wide&Deep的Wide側進行了改進。之前的Wide是一個LR,輸入是離散特徵和互動特徵,互動特徵會依賴人工特徵工程來做cross。DeepFM則是用FM來代替了互動特徵的部分,和Wide&Deep相比不再依賴特徵工程,同時cross-column的剔除可以降低輸入的維度。
和PNN/FNN相比,DeepFM能更多提取到到低階特徵。而且上述這些模型間直接並不互斥,比如把DeepFM的FMLayer共享到Deep部分其實就是IPNN。
模型
Wide部分就是一個FM,輸入是N個one-hot的離散特徵,每個離散特徵對應到等長的低維(k)embedding上,最終輸出的就是之前FM模型的output。並且因為這裡不需要像IPNN一樣輸出隱向量,因此可以使用FM降低複雜度的trick。

Deep部分和Wide部分共享N*K的Embedding輸入層,然後跟兩個全聯接層

Deep和Wide聯合訓練,模型最終的輸出是FM部分和Deep部分權重為1的簡單加和。聯合訓練共享Embedding也保證了二階特徵互動學到的Embedding會和高階資訊學到的Embedding的一致性。
程式碼實現
@tf_estimator_model
def model_fn(features, labels, mode, params):
dense_feature, sparse_feature = build_features()
dense = tf.feature_column.input_layer(features, dense_feature)
sparse = tf.feature_column.input_layer(features, sparse_feature)
with tf.variable_scope('FM_component'):
with tf.variable_scope( 'Linear' ):
linear_output = tf.layers.dense(sparse, units=1)
add_layer_summary( 'linear_output', linear_output )
with tf.variable_scope('second_order'):
# reshape (batch_size, n_feature * emb_size) -> (batch_size, n_feature, emb_size)
emb_size = dense_feature[0].variable_shape.as_list()[0] # all feature has same emb dimension
embedding_matrix = tf.reshape(dense, (-1, len(dense_feature), emb_size))
add_layer_summary( 'embedding_matrix', embedding_matrix )
# Compared to FM embedding here is flatten(x * v) not v
sum_square = tf.pow( tf.reduce_sum( embedding_matrix, axis=1 ), 2 )
square_sum = tf.reduce_sum( tf.pow(embedding_matrix,2), axis=1 )
fm_output = tf.reduce_sum(tf.subtract( sum_square, square_sum) * 0.5, axis=1, keepdims=True)
add_layer_summary('fm_output', fm_output)
with tf.variable_scope('Deep_component'):
for i, unit in enumerate(params['hidden_units']):
dense = tf.layers.dense(dense, units = unit, activation ='relu', name = 'dense{}'.format(i))
dense = tf.layers.batch_normalization(dense, center=True, scale = True, trainable=True,
training=(mode ==tf.estimator.ModeKeys.TRAIN))
dense = tf.layers.dropout( dense, rate=params['dropout_rate'], training = (mode==tf.estimator.ModeKeys.TRAIN))
add_layer_summary( dense.name, dense )
with tf.variable_scope('output'):
y = dense + fm_output + linear_output
add_layer_summary( 'output', y )
return y
等處理好另一份樣本, 會把程式碼更新成匹配高維稀疏特徵feat_id:feat_val輸入格式的。完整程式碼在這裡 https://github.com/DSXiangLi/CTR
CTR學習筆記&程式碼實現系列
