CTR學習筆記系列的第一篇，總結在深度模型稱王之前經典LR，FM, FFM模型，這些經典模型後續也作為元件用於各個深度模型。模型分別用自定義Keras Layer和estimator來實現，哈哈一個是舊愛一個是新歡。特徵工程依賴feature_column實現，這裡做的比較簡單在後面的深度模型再好好搞。完整程式碼在這裡https://github.com/DSXiangLi/CTR ## 問題定義 CTR本質是一個二分類問題，$X \in R^N $是使用者和廣告相關特徵, $Y \in (0,1)$是每個廣告是否被點選，基礎模型就是一個簡單的Logistics Regression $$ P(Y=1) = \frac{1}{1+ exp{(w_0 + \sum_{i=1}^Nw_ix_i)}} $$ 考慮在之後TF框架裡logistics可以簡單用activation來表示，我們把核心的部分簡化為以下 $$ y(x) = w_0 + \sum_{i=1}^Nw_ix_i $$

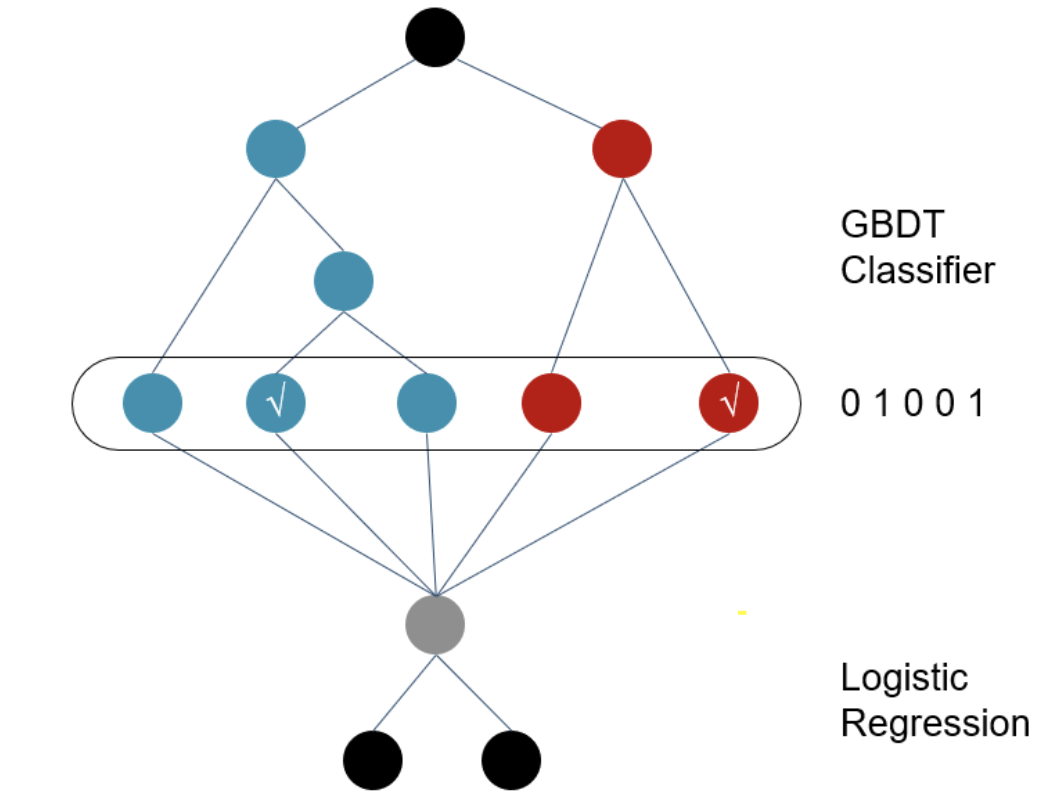
## LR模型 2010年之前主流的CTR模型通常是最簡單的logistics regression，模型可解釋性強，工程上部署簡單快捷。但最大的問題是依賴於大量的手工特徵工程。 剛接觸特徵工程的同學可能會好奇為什麼需要計算組合特徵？ 最開始我只是簡單認為越細粒度的聚合特徵Bias越小。接觸了因果推理後，我覺得更適合用**Simpson Paradox**裡的**Confounder Bias**來解釋，不同聚合特徵之間可能會相悖，例如各個年齡段的男性點選率均低於女性，但整體上男性的點選率高於女性。感興趣的可以看看這篇部落格[因果推理的春天系列序 - 資料探勘中的Confounding, Collidar, Mediation Bias][1] 如果即想簡化特徵工程，又想加入特徵組合，肯定就會想到下面的暴力特徵組合方式。這個也被稱作POLY2模型 $$ y(x) = w_0 + \sum_{i=1}^N w_ix_i + \sum_{i=1}^N \sum_{j=i+1}^N w_{i,j} x_ix_j $$ 但上述$w_{i,j}$需要學習$\frac{n(n-1)}{2}$個引數，一方面複雜度高，另一方面對高維稀疏特徵會出現大量$w_{i,j}$是0的情況，模型無法學到樣本中未曾出現的特徵組合pattern，模型泛化性差。 於是**降低複雜度，自動選擇有效特徵組合，以及模型泛化**這三點成為後續主要的改進的方向。 ## GBDT+LR模型 2014年Facebook提出在GBDT疊加LR的方法，敲開了**特徵工程模型化**的大門。GBDT輸出的不是預測概率，而是每一個樣本落在每一顆子樹哪個葉節點的一個0/1矩陣。在只保留和target相關的有效特徵組合的同時，避免了手工特徵組合需要的業務理解和人工成本。 相較特徵組合，我更喜歡把GBDT輸出的特徵向量，理解為根據target，對樣本進行了聚類/降維，輸出的是該樣本所屬的幾個特定人群組合，每一棵子樹都對應一種型別的人群組合。 但是！GBDT依舊存在泛化問題，因為所有葉節點的選擇都依賴於訓練樣本，並且GBDT在離散特徵上效果比較有限。同時也存在經過GBDT變換得到的特徵依舊是高維稀疏特徵的問題。

## FM模型 2010年Rendall提出的因子分解機模型(FM)為降低計算複雜度，為增加模型泛化能力提供了思路 ### 原理 FM模型將上述暴力特徵組合直接求解整個權重矩$w_ij \in R^{N*N}$，轉化為求解權重矩陣的隱向量$V \in R^{N*k}$，這一步會大大增加模型泛化能力，因為權重矩陣不再完全依賴於樣本中的特定特徵組合，而是可以通過特徵間的相關關係間接得到。 同時隱向量把模型需要學習的引數數量從$\frac{n(n-1)}{2}$降低到$nk$個 $$ \begin{align} y(x) & = w_0 + \sum_{i=1}^Nw_i x_i + \sum_{i=1}^N \sum_{j=i+1}^N w_{i,j} x_ix_j\\ &= w_0 + \sum_{i=1}^Nw_i x_i + \sum_{i=1}^N \sum_{j=i+1}^N