寫給程式設計師的機器學習入門 (三) - 線性模型,啟用函式與多層線性模型
生物神經元與人工神經元
在瞭解神經元網路之前,我們先簡單的看看生物學上的神經元是什麼樣子的,下圖摘自維基百科:
(因為我不是專家,這裡的解釋只用於理解人工神經元模擬了生物神經元的什麼地方,不一定完全準確)
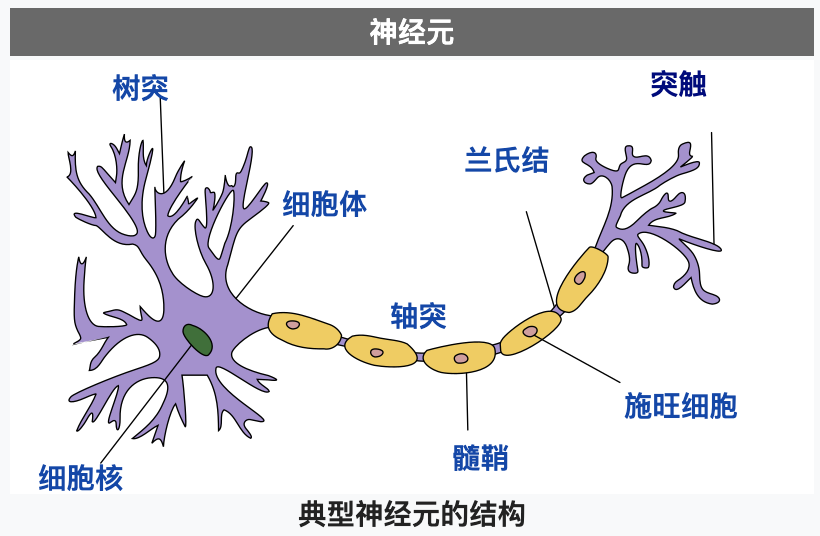
神經元主要由細胞體和細胞突組成,而細胞突分為樹突 (Dendrites) 和軸突 (Axon),樹突負責接收其他神經元輸入的電流,而軸突負責把電流輸出給其他神經元。一個神經元可以通過樹突從多個神經元接收電流,如果電流沒有達到某個閾值則神經元不會把電流輸出,如果電流達到了某個閾值則神經元會通過軸突的突觸把電流輸出給其他神經元,這樣的規則被稱為全有全無律。輸入電流達到閾值以後輸出電流的狀態又稱為到達動作電位,動作電位會持續 1 ~ 2 毫秒,之後會進入約 0.5 毫秒的絕對不應期,無論輸入多大的電流都不會輸出,然後再進入約 3.5 毫秒的相對不應期,需要電流達到更大的閾值才會輸出,最後返回靜息電位。神經元之間連線起來的網路稱為神經元網路,人的大腦中大約有 860 億個神經元,因為 860 億個神經元可以同時工作,所以目前的計算機無法模擬這種工作方式 (除非開發專用的晶片),只能模擬一部分的工作方式和使用更小規模的網路。
計算機模擬神經元網路使用的是人工神經元,單個人工神經元可以用以下公式表達:
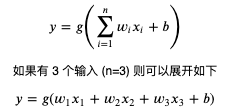
其中 n 代表輸入的個數,你可以把 n 看作這個神經元擁有的樹突個數,x 看作每個樹突輸入電流的值;而 w (weight) 代表各個輸入的權重,也就是各個樹突對電流大小的調整;而 b (bias) 用於調整各個輸入乘權重相加後的值,使得這個值可以配合某個閾值工作;而 g 則是啟用函式,用於判斷值是否達到閾值並輸出和輸出多少,通常會使用非線性函式;而 y 則是輸出的值,可以把它看作軸突輸出的電流,連線這個 y 到其他神經元就可以組建神經元網路。
我們在前兩篇看到的其實就是隻有一個輸入並且沒有啟用函式的單個人工神經元,把同樣的輸入傳給多個神經元 (第一層),然後再傳給其他神經元 (第二層),然後再傳給其他神經元 (第三層) 就可以組建人工神經元網路了,同一層的神經元個數越多,神經元的層數越多,網路就越強大,但需要更多的運算時間並且更有可能發生第一篇文章講過的過擬合 (Overfitting) 現象。
下圖是人工神經元網路的例子,有 3 輸入 1 個輸出,經過 3 層處理,第 1 層和第 2 層各有兩個神經元對應隱藏值 (中間值),第 3 層有一個神經元對應輸出值:
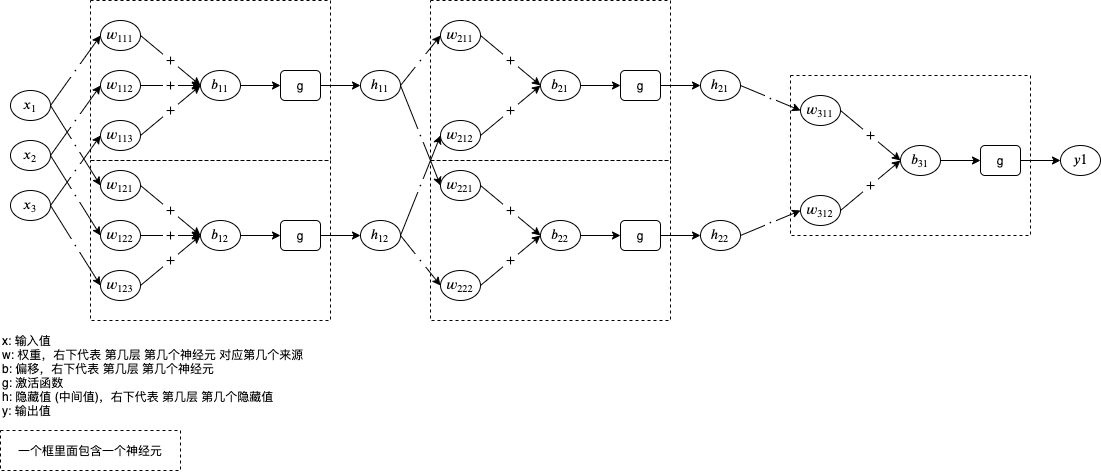
神經元中包含的 w 和 b 就是我們需要通過機器學習調整的引數值。
如果你覺得圖片有點難以理解,可以看轉換後的程式碼:
h11 = g(x1 * w111 + x2 * w112 + x3 * w113 + b11) h12 = g(x1 * w121 + x2 * w122 + x3 * w123 + b12) h21 = g(h11 * w211 + h12 * w212 + b21) h22 = g(h11 * w221 + h12 * w222 + b22) y = g(h21 * w311 + h22 * w312 + b31)
很多痴迷人工神經元網路的學者聲稱人工神經元網路可以模擬人腦的工作方式,做到某些領域上超過人腦的判斷,但實際上這還有很大的爭議,我們可以看到人工神經元的連線方式只會按固定的模式,判斷是否達到閾值並輸出的邏輯也無法做到和生物神經元一樣(目前還沒有解明),並且也沒有生物神經元的不應期,所以也有學者聲稱人工神經元不過只是做了複雜的數學運算來模擬邏輯判斷,需要根據不同的場景切換不同的計算方法,使用這種方式並不能達到人腦的水平。
單層線性模型
在前一篇文章我們已經稍微瞭解過機器學習框架 pytorch,現在我們來看看怎麼使用 pytorch 封裝的線性模型,以下程式碼執行在 python 的 REPL 中:
# 匯入 pytorch 類庫
>>> import torch
# 建立 pytorch 封裝的線性模型,設定輸入有 3 個輸出有 1 個
>>> model = torch.nn.Linear(in_features=3, out_features=1)
# 檢視線性模型內部包含的引數列表
# 這裡一共包含兩個引數,第一個引數是 1 行 3 列的矩陣分別表示 3 個輸入對應的 w 值 (權重),第二個引數表示 b 值 (偏移)
# 初始值會隨機生成 (使用 kaiming_uniform 生成正態分佈)
>>> list(model.parameters())
[Parameter containing:
tensor([[0.0599, 0.1324, 0.0099]], requires_grad=True), Parameter containing:
tensor([-0.2772], requires_grad=True)]
# 定義輸入和輸出
>>> x = torch.tensor([1, 2, 3], dtype=torch.float)
>>> y = torch.tensor([6], dtype=torch.float)
# 把輸入傳給模型
>>> p = model(x)
# 檢視預測輸出值
# 1 * 0.0599 + 2 * 0.1324 + 3 * 0.0099 - 0.2772 = 0.0772
>>> p
tensor([0.0772], grad_fn=<AddBackward0>)
# 計算誤差並自動微分
>>> l = (p - y).abs()
>>> l
tensor([5.9228], grad_fn=<AbsBackward>)
>>> l.backward()
# 檢視各個引數對應的導函式值
>>> list(model.parameters())[0].grad
tensor([[-1., -2., -3.]])
>>> list(model.parameters())[1].grad
tensor([-1.])
以上可以看作 1 層 1 個神經元,很好理解吧?我們來看看 1 層 2 個神經元:
# 匯入 pytorch 類庫
>>> import torch
# 建立 pytorch 封裝的線性模型,設定輸入有 3 個輸出有 2 個
>>> model = torch.nn.Linear(in_features=3, out_features=2)
# 檢視線性模型內部包含的引數列表
# 這裡一共包含兩個引數
# 第一個引數是 2 行 3 列的矩陣分別表示 2 個輸出和 3 個輸入對應的 w 值 (權重)
# 第二個引數表示 2 個輸出對應的 b 值 (偏移)
>>> list(model.parameters())
[Parameter containing:
tensor([[0.1393, 0.5165, 0.2910],
[0.2276, 0.1579, 0.1958]], requires_grad=True), Parameter containing:
tensor([0.2566, 0.1701], requires_grad=True)]
# 定義輸入和輸出
>>> x = torch.tensor([1, 2, 3], dtype=torch.float)
>>> y = torch.tensor([6, -6], dtype=torch.float)
# 把輸入傳給模型
>>> p = model(x)
# 檢視預測輸出值
# 1 * 0.1393 + 2 * 0.5165 + 3 * 0.2910 + 0.2566 = 2.3019
# 1 * 0.2276 + 2 * 0.1579 + 3 * 0.1958 + 0.1701 = 1.3009
>>> p
tensor([2.3019, 1.3009], grad_fn=<AddBackward0>)
# 計算誤差並自動微分
# (abs(2.3019 - 6) + abs(1.3009 - -6)) / 2 = 5.4995
>>> l = (p - y).abs().mean()
>>> l
tensor(5.4995, grad_fn=<MeanBackward0>)
>>> l.backward()
# 檢視各個引數對應的導函式值
# 因為誤差取了 2 個值的平均,所以求導函式值的時候會除以 2
>>> list(model.parameters())[0].grad
tensor([[-0.5000, -1.0000, -1.5000],
[ 0.5000, 1.0000, 1.5000]])
>>> list(model.parameters())[1].grad
tensor([-0.5000, 0.5000])
現在我們來試試用線性模型來學習符合 x_1 * 1 + x_2 * 2 + x_3 * 3 + 8 = y 的資料,輸入和輸出會使用矩陣定義:
# 引用 pytorch
import torch
# 給隨機數生成器分配一個初始值,使得每次執行都可以生成相同的隨機數
# 這是為了讓訓練過程可重現,你也可以選擇不這樣做
torch.random.manual_seed(0)
# 建立線性模型,設定有 3 個輸入 1 個輸出
model = torch.nn.Linear(in_features=3, out_features=1)
# 建立損失計算器
loss_function = torch.nn.MSELoss()
# 建立引數調整器
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 隨機生成原始資料集,一共 20 組資料,每條資料有 3 個輸入
dataset_x = torch.randn((20, 3))
dataset_y = dataset_x.mm(torch.tensor([[1], [2], [3]], dtype=torch.float)) + 8
print(f"dataset_x: {dataset_x}")
print(f"dataset_y: {dataset_y}")
# 切分訓練集 (12 組),驗證集 (4 組) 和測試集 (4 組)
random_indices = torch.randperm(dataset_x.shape[0])
traning_indices = random_indices[:int(len(random_indices)*0.6)]
validating_indices = random_indices[int(len(random_indices)*0.6):int(len(random_indices)*0.8):]
testing_indices = random_indices[int(len(random_indices)*0.8):]
traning_set_x = dataset_x[traning_indices]
traning_set_y = dataset_y[traning_indices]
validating_set_x = dataset_x[validating_indices]
validating_set_y = dataset_y[validating_indices]
testing_set_x = dataset_x[testing_indices]
testing_set_y = dataset_y[testing_indices]
# 開始訓練過程
for epoch in range(1, 10000):
print(f"epoch: {epoch}")
# 根據訓練集訓練並修改引數
# 切換模型到訓練模式,將會啟用自動微分,批次正規化 (BatchNorm) 與 Dropout
model.train()
# 計算預測值
# 20 行 3 列的矩陣乘以 3 行 1 列的矩陣 (由 weight 轉置得到) 等於 20 行 1 列的矩陣
predicted = model(traning_set_x)
# 計算損失
loss = loss_function(predicted, traning_set_y)
# 列印除錯資訊
print(f"loss: {loss}, weight: {model.weight}, bias: {model.bias}")
# 從損失自動微分求導函式值
loss.backward()
# 使用引數調整器調整引數
optimizer.step()
# 清空導函式值
optimizer.zero_grad()
# 檢查驗證集
# 切換模型到驗證模式,將會禁用自動微分,批次正規化 (BatchNorm) 與 Dropout
model.eval()
predicted = model(validating_set_x)
validating_accuracy = 1 - ((validating_set_y - predicted).abs() / validating_set_y).abs().mean()
print(f"validating x: {validating_set_x}, y: {validating_set_y}, predicted: {predicted}")
# 如果驗證集正確率大於 99 %,則停止訓練
print(f"validating accuracy: {validating_accuracy}")
if validating_accuracy > 0.99:
break
# 檢查測試集
predicted = model(testing_set_x)
testing_accuracy = 1 - ((testing_set_y - predicted).abs() / testing_set_y).abs().mean()
print(f"testing x: {testing_set_x}, y: {testing_set_y}, predicted: {predicted}")
print(f"testing accuracy: {testing_accuracy}")
輸出結果如下:
dataset_x: tensor([[ 0.8487, 0.6920, -0.3160],
[-2.1152, -0.3561, 0.4372],
[ 0.4913, -0.2041, 0.1198],
[ 1.2377, 1.1168, -0.2473],
[-1.0438, -1.3453, 0.7854],
[ 0.9928, 0.5988, -1.5551],
[-0.3414, 1.8530, 0.4681],
[-0.1577, 1.4437, 0.2660],
[ 1.3894, 1.5863, 0.9463],
[-0.8437, 0.9318, 1.2590],
[ 2.0050, 0.0537, 0.4397],
[ 0.1124, 0.6408, 0.4412],
[-0.2159, -0.7425, 0.5627],
[ 0.2596, 0.5229, 2.3022],
[-1.4689, -1.5867, -0.5692],
[ 0.9200, 1.1108, 1.2899],
[-1.4782, 2.5672, -0.4731],
[ 0.3356, -1.6293, -0.5497],
[-0.4798, -0.4997, -1.0670],
[ 1.1149, -0.1407, 0.8058]])
dataset_y: tensor([[ 9.2847],
[ 6.4842],
[ 8.4426],
[10.7294],
[ 6.6217],
[ 5.5252],
[12.7689],
[11.5278],
[15.4009],
[12.7970],
[11.4315],
[10.7175],
[ 7.9872],
[16.2120],
[ 1.6500],
[15.0112],
[10.2369],
[ 3.4277],
[ 3.3199],
[11.2509]])
epoch: 1
loss: 142.77590942382812, weight: Parameter containing:
tensor([[-0.0043, 0.3097, -0.4752]], requires_grad=True), bias: Parameter containing:
tensor([-0.4249], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[-0.1385],
[ 0.3020],
[-0.0126],
[-1.1801]], grad_fn=<AddmmBackward>)
validating accuracy: -0.04714548587799072
epoch: 2
loss: 131.40403747558594, weight: Parameter containing:
tensor([[ 0.0675, 0.4937, -0.3163]], requires_grad=True), bias: Parameter containing:
tensor([-0.1970], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[-0.2023],
[ 0.6518],
[ 0.3935],
[-1.1479]], grad_fn=<AddmmBackward>)
validating accuracy: -0.03184401988983154
epoch: 3
loss: 120.98343658447266, weight: Parameter containing:
tensor([[ 0.1357, 0.6687, -0.1639]], requires_grad=True), bias: Parameter containing:
tensor([0.0221], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[-0.2622],
[ 0.9860],
[ 0.7824],
[-1.1138]], grad_fn=<AddmmBackward>)
validating accuracy: -0.016991496086120605
省略途中輸出
epoch: 637
loss: 0.001102567883208394, weight: Parameter containing:
tensor([[1.0044, 2.0283, 3.0183]], requires_grad=True), bias: Parameter containing:
tensor([7.9550], requires_grad=True)
validating x: tensor([[-0.4798, -0.4997, -1.0670],
[ 0.8487, 0.6920, -0.3160],
[ 0.1124, 0.6408, 0.4412],
[-1.0438, -1.3453, 0.7854]]), y: tensor([[ 3.3199],
[ 9.2847],
[10.7175],
[ 6.6217]]), predicted: tensor([[ 3.2395],
[ 9.2574],
[10.6993],
[ 6.5488]], grad_fn=<AddmmBackward>)
validating accuracy: 0.9900396466255188
testing x: tensor([[-0.3414, 1.8530, 0.4681],
[-1.4689, -1.5867, -0.5692],
[ 1.1149, -0.1407, 0.8058],
[ 0.3356, -1.6293, -0.5497]]), y: tensor([[12.7689],
[ 1.6500],
[11.2509],
[ 3.4277]]), predicted: tensor([[12.7834],
[ 1.5438],
[11.2217],
[ 3.3285]], grad_fn=<AddmmBackward>)
testing accuracy: 0.9757462739944458
可以看到最終 weight 接近 1, 2, 3,bias 接近 8。和前一篇文章最後的例子比較還可以發現程式碼除了定義模型的部分以外幾乎一模一樣 (後面的程式碼基本上都是相同的結構,這個系列是先學套路在學細節
