opencv-12-高斯濾波-雙邊濾波(附C++程式碼實現)
阿新 • • 發佈:2020-05-10
## 開始之前
這幾天由於自己的原因沒有寫, 一個是因為自己懶了, 一個是感覺這裡遇到點問題不想往下寫了, 我們先努力結束這個章節吧, 之前介紹了比較常用而且比較好理解的均值和中值濾波, 但是呢,在例程[Smoothing Images](https://docs.opencv.org/4.3.0/dc/dd3/tutorial_gausian_median_blur_bilateral_filter.html), 還有給出的其他的濾波方式, 主要是高斯濾波和雙邊濾波,
我們這一次完結掉濾波與平滑的這個部分, 寫的有點多了,反而不想再寫了, 加油
[toc]
## 本文目標
本文主要是介紹
- 高斯濾波
- 雙邊濾波
和之前介紹的一樣, 我們仍然還是 介紹一下原理, 給出一下具體的形式, 然後使用 opencv 進行一下實現的過程, 最後使用我們之前的影象進行測試 進行演算法的分析與總結.
## 正文
### 高斯濾波(Gaussian Filter)
我們在之前介紹了中值濾波是統計排序的結果, 屬於非線性的結果, 均值濾波是使用模板核進行的操作, 我們在的文章中也提到了均值濾波在計算的過程中必須要考慮權重的問題, 進而提出了加權的均值濾波的操作, 比如最常見的加權均值濾波的操作核.
$$
M = \frac{1}{16} \left [
\begin{array}{c}
1 & 2 & 1 \\ 2& 4 & 2 \\ 1 & 2 & 1
\end{array}
\right ]
$$
其實呢,這個核也就是高斯濾波器在 `3*3`視窗的離散取整的結果值, 最明顯的特點就是模板的係數隨著距離模板中心的距離而變換, 能夠有效的抑制噪聲,平滑影象, 相比均值濾波能夠更好的平滑影象, 保留影象邊緣.
#### 高斯濾波原理
由於我們的影象是二維的, 但是高斯分佈是一維的, 那我們先考慮一維的高斯分佈, 就是我們常用的正太分佈曲線,
$$
G(x) = \frac{1}{\sqrt{2\pi \sigma}} e^{-\frac{x^2}{2\sigma^2}}
$$
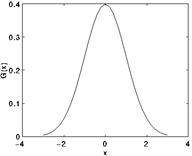
對於二維的高斯分佈其實可以考慮成兩個方向的運算相疊加的得到的結果
$$
G(x,y) = \frac{1}{2\pi \sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}} = G(x)*G(y)
$$
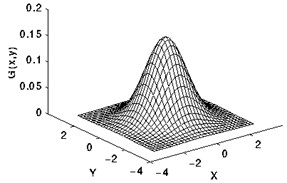
考慮到影象的計算實際上是離散的座標, 對於視窗大小為 $(2k + 1) \times (2k + 1)$ 模板, 我們可以表示成
$$
G{i,j} = \frac{1}{2\pi \sigma ^ 2}e ^{-\frac{(i - k - 1)^2 + (j - k - 1)^2}{2 \sigma ^ 2}}
$$
可以參考[影象處理基礎(4):高斯濾波器詳解](https://www.cnblogs.com/wangguchangqing/p/6407717.html)
裡面給出的方法, 使用
```cpp
void generateGaussianTemplate(double window[][11], int ksize, double sigma)
{
static const double pi = 3.1415926;
int center = ksize / 2; // 模板的中心位置,也就是座標的原點
double x2, y2;
for (int i = 0; i < ksize; i++)
{
x2 = pow(i - center, 2);
for (int j = 0; j < ksize; j++)
{
y2 = pow(j - center, 2);
double g = exp(-(x2 + y2) / (2 * sigma * sigma));
g /= 2 * pi * sigma*sigma; //
window[i][j] = g;
}
}
double k = 1 / window[0][0]; // 將左上角的係數歸一化為1
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
window[i][j] *= k;
}
}
}
```
生成了$3 \times 3, \sigma = 0.8$ 的高斯模板, 對應的將其取整就得到了
$$
M = \frac{1}{16} \left [
\begin{array}{c}
1 & 2 & 1 \\ 2& 4 & 2 \\ 1 & 2 & 1
\end{array}
\right ]
$$
上面給出的文章同樣的詳細介紹了 $\sigma$ 在統計學中的意義, 可以去參考學習
不過根據高中的知識, 我們可以看到 正態分佈的曲線
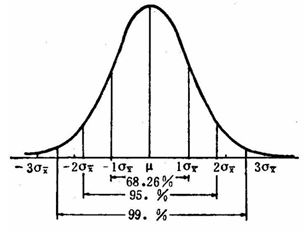
#### C++ 實現
在我們之前提到的[影象處理基礎(4):高斯濾波器詳解](https://www.cnblogs.com/wangguchangqing/p/6407717.html) 這裡給出了基於 opencv 的程式碼實現, 這裡是$O(m*n*k^2)$ 的演算法實現
```cpp
// 來源連結: https://www.cnblogs.com/wangguchangqing/p/6407717.html
void GaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma)
{
CV_Assert(src.channels() || src.channels() == 3); // 只處理單通道或者三通道影象
const static double pi = 3.1415926;
// 根據視窗大小和sigma生成高斯濾波器模板
// 申請一個二維陣列,存放生成的高斯模板矩陣
double **templateMatrix = new double*[ksize];
for (int i = 0; i < ksize; i++)
templateMatrix[i] = new double[ksize];
int origin = ksize / 2; // 以模板的中心為原點
double x2, y2;
double sum = 0;
for (int i = 0; i < ksize; i++)
{
x2 = pow(i - origin, 2);
for (int j = 0; j < ksize; j++)
{
y2 = pow(j - origin, 2);
// 高斯函式前的常數可以不用計算,會在歸一化的過程中給消去
double g = exp(-(x2 + y2) / (2 * sigma * sigma));
sum += g;
templateMatrix[i][j] = g;
}
}
for (int i = 0; i < ksize; i++)
{
for (int j = 0; j < ksize; j++)
{
templateMatrix[i][j] /= sum;
cout << templateMatrix[i][j] << " ";
}
cout << endl;
}
// 將模板應用到影象中
int border = ksize / 2;
copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT);
int channels = dst.channels();
int rows = dst.rows - border;
int cols = dst.cols - border;
for (int i = border; i < rows; i++)
{
for (int j = border; j < cols; j++)
{
double sum[3] = { 0 };
for (int a = -border; a <= border; a++)
{
for (int b = -border; b <= border; b++)
{
if (channels == 1)
{
sum[0] += templateMatrix[border + a][border + b] * dst.at(i + a, j + b);
}
else if (channels == 3)
{
Vec3b rgb = dst.at(i + a, j + b);
auto k = templateMatrix[border + a][border + b];
sum[0] += k * rgb[0];
sum[1] += k * rgb[1];
sum[2] += k * rgb[2];
}
}
}
for (int k = 0; k < channels; k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (channels == 1)
dst.at(i, j) = static_cast(sum[0]);
else if (channels == 3)
{
Vec3b rgb = { static_cast(sum[0]), static_cast(sum[1]), static_cast(sum[2]) };
dst.at(i, j) = rgb;
}
}
}
// 釋放模板陣列
for (int i = 0; i < ksize; i++)
delete[] templateMatrix[i];
delete[] templateMatrix;
}
```
然後同樣的給出了分離的實現, 將影象進行水平運算之後再進行豎直運算, 計算的時間上會有一定的速度提升
```cpp
// 來源連結: https://www.cnblogs.com/wangguchangqing/p/6407717.html
// 分離的計算
void separateGaussianFilter(const Mat &src, Mat &dst, int ksize, double sigma)
{
CV_Assert(src.channels()==1 || src.channels() == 3); // 只處理單通道或者三通道影象
// 生成一維的高斯濾波模板
double *matrix = new double[ksize];
double sum = 0;
int origin = ksize / 2;
for (int i = 0; i < ksize; i++)
{
// 高斯函式前的常數可以不用計算,會在歸一化的過程中給消去
double g = exp(-(i - origin) * (i - origin) / (2 * sigma * sigma));
sum += g;
matrix[i] = g;
}
// 歸一化
for (int i = 0; i < ksize; i++)
matrix[i] /= sum;
// 將模板應用到影象中
int border = ksize / 2;
copyMakeBorder(src, dst, border, border, border, border, BorderTypes::BORDER_REFLECT);
int channels = dst.channels();
int rows = dst.rows - border;
int cols = dst.cols - border;
// 水平方向
for (int i = border; i < rows; i++)
{
for (int j = border; j < cols; j++)
{
double sum[3] = { 0 };
for (int k = -border; k <= border; k++)
{
if (channels == 1)
{
sum[0] += matrix[border + k] * dst.at(i, j + k); // 行不變,列變化;先做水平方向的卷積
}
else if (channels == 3)
{
Vec3b rgb = dst.at(i, j + k);
sum[0] += matrix[border + k] * rgb[0];
sum[1] += matrix[border + k] * rgb[1];
sum[2] += matrix[border + k] * rgb[2];
}
}
for (int k = 0; k < channels; k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (channels == 1)
dst.at(i, j) = static_cast(sum[0]);
else if (channels == 3)
{
Vec3b rgb = { static_cast(sum[0]), static_cast(sum[1]), static_cast(sum[2]) };
dst.at(i, j) = rgb;
}
}
}
// 豎直方向
for (int i = border; i < rows; i++)
{
for (int j = border; j < cols; j++)
{
double sum[3] = { 0 };
for (int k = -border; k <= border; k++)
{
if (channels == 1)
{
sum[0] += matrix[border + k] * dst.at(i + k, j); // 列不變,行變化;豎直方向的卷積
}
else if (channels == 3)
{
Vec3b rgb = dst.at(i + k, j);
sum[0] += matrix[border + k] * rgb[0];
sum[1] += matrix[border + k] * rgb[1];
sum[2] += matrix[border + k] * rgb[2];
}
}
for (int k = 0; k < channels; k++)
{
if (sum[k] < 0)
sum[k] = 0;
else if (sum[k] > 255)
sum[k] = 255;
}
if (channels == 1)
dst.at(i, j) = static_cast(sum[0]);
else if (channels == 3)
{
Vec3b rgb = { static_cast(sum[0]), static_cast(sum[1]), static_cast(sum[2]) };
dst.at(i, j) = rgb;
}
}
}
delete[] matrix;
}
```
這裡的演算法都是 上面提到的https://www.cnblogs.com/wangguchangqing/p/6407717.html 這篇文章, 具體可以去看內容
#### opencv 高斯濾波
其實這篇文章[影象處理--高斯濾波](https://blog.csdn.net/L_inYi/article/details/8915116)寫的很好
其實主要的結構也就是他給出的過程
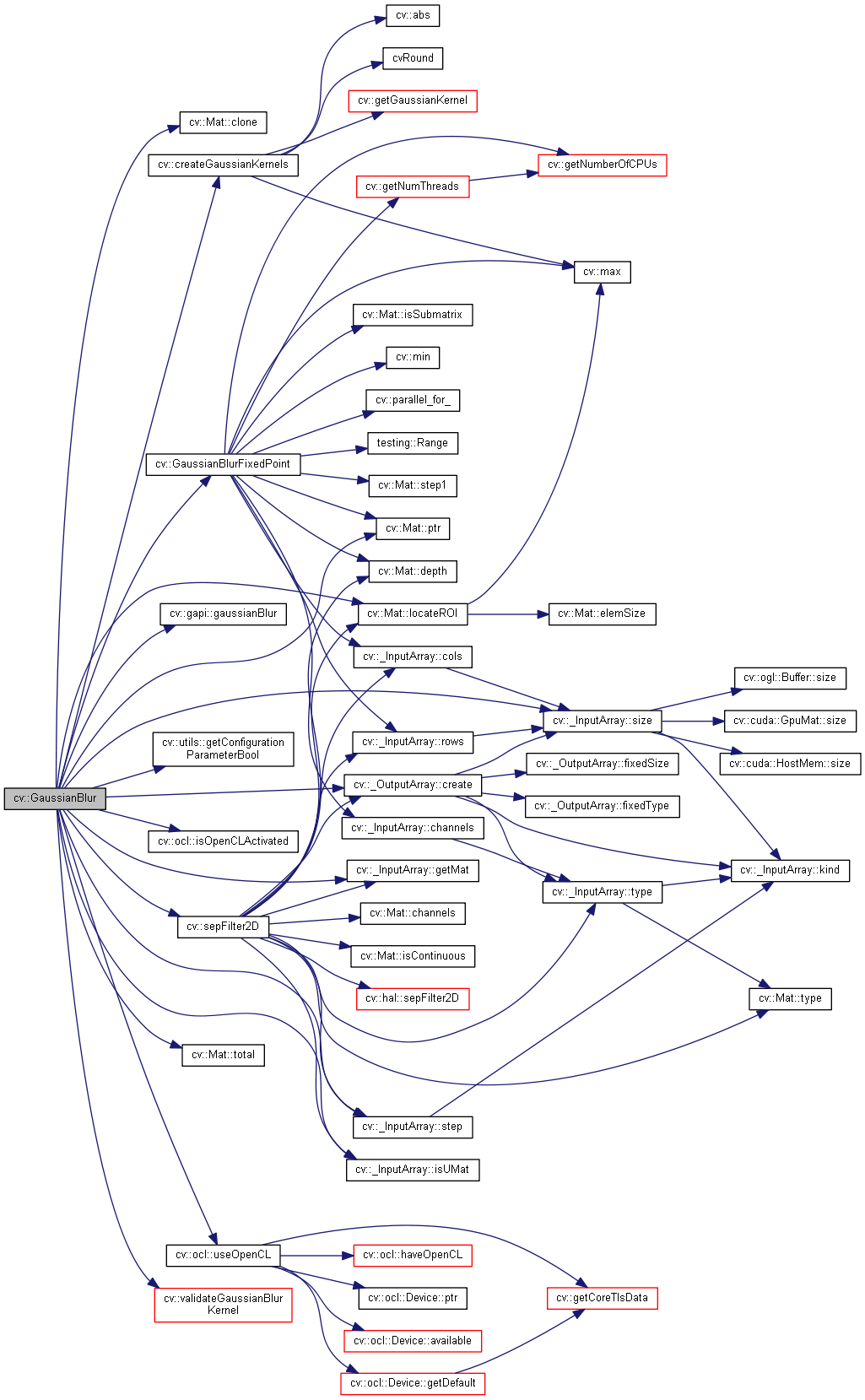
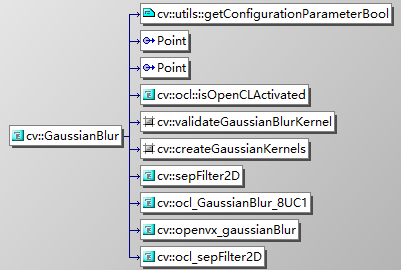
其實整個高斯濾波的過程就是建立高斯核, 然後使用 filter2D 的方法進行的濾波操作, 具體要深入的話可以看函式的呼叫圖, 實現起來也是一樣的思路, 很簡單的操作, 我們之後測試一下效果..
```cpp
// /modules\imgproc\src\smooth.dispatch.cpp:600
void GaussianBlur(InputArray _src, OutputArray _dst, Size ksize,
double sigma1, double sigma2,
int borderType)
```
- src 輸入影象
- dst 輸出影象
- ksize 核的尺寸 奇數
- sigmaX x 方向 的 sigma 值
- sigmaY y 方向 的 sigma 值
- borderType 邊界處理的方式
#### 高斯濾波效果對比
我們還是使用之前的高椒鹽噪聲影象, 然後直接進行演算法濾波, 計算結果就好, 跟之前的測試影象很相似, 這裡

這裡的四張圖分別對應 高噪聲影象, 直接高斯濾波的結果, 分離xy方向進行濾波結果,以及opencv 自帶的高斯濾波效果圖, 這裡是預覽影象, 實際的檢測結果就是上面給出的引數值, 實際上效果只能說一般, 我們之後再進行演算法層面的對比.
```bash
image-noise: psnr:19.4727, mssim: B:0.353134 G:0.383638 R:0.629353
image-noise: psnr:26.3155, mssim: B:0.584585 G:0.617172 R:0.812303
image-noise: psnr:26.1721, mssim: B:0.574719 G:0.607494 R:0.809844
image-noise: psnr:26.4206, mssim: B:0.598176 G:0.630657 R:0.819658
```
### 雙邊濾波(Bilateral Filter)
#### 雙邊濾波原理
我們在上面提出了高斯濾波的原理是對於距離模板中心 距離不同給予不同的權重, 而雙邊濾波則不僅考慮影象的空間距離, 還要考慮其灰度距離, 對於越接近中間灰度值的點權重越高, 灰度值相差大的則權重更小.
雙邊濾波的原理可以參考[雙邊濾波(Bilateral Filter)詳解](https://blog.csdn.net/Jfuck/article/details/8932978),
可以參考[Bilateral Filtering for Gray and Color Images](http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html)
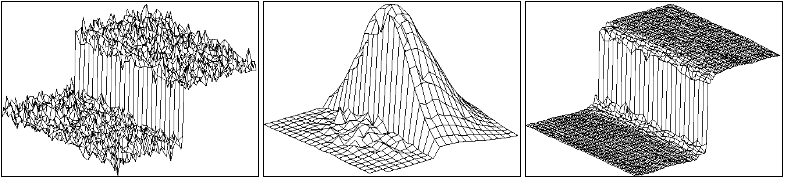
在文章[影象處理基礎(5):雙邊濾波器](https://www.cnblogs.com/wangguchangqing/p/6416401.html)詳細介紹了雙邊濾波
其實跟上面給出的濾波演示一致, 都是在保證影象邊緣資訊的情況下進行噪聲的濾波..
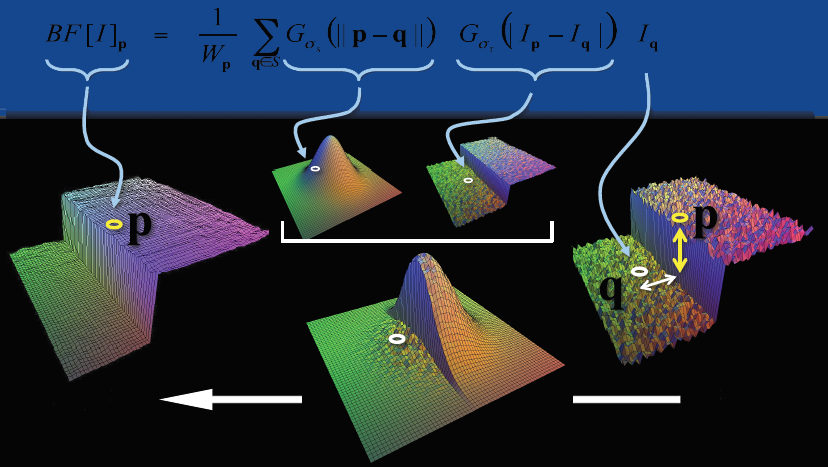
可以參考[bilateral filter雙邊濾波器的通俗理解](https://blog.csdn.net/guyuealian/article/details/82660826) 給出的雙邊濾波的數學表達
$$
g(x,y) = \frac{\sum_{kl}f(k,l)w(i,j,k,l)}{\sum_{kl}w(i,j,k,l)}
$$
對於不同的模板係數又有兩個部分, 主要是 空間域模板權值 $w_d$ 和 灰度域 模板權值 $w_r$,
$$
\begin{array}{rl}
w_d(i,j,k,l) &= e^{-\frac{(i-k)^2 +(j-l)^2}{2\sigma_d^2}} \\
w_r(i,j,k,l) &= e^{-\frac{\left \| f(i,j) - f(k,l) \right \|} {2\sigma_r^2}} \\
w &= w_d * w_r
\end{array}
$$
其中,$q(i,j)$ 為模板視窗的其他係數的座標,$f(i,j)$ 表示影象在點$q(i,j)$ 處的畫素值;$p(k,l)$ 為模板視窗的中心座標點,對應的畫素值為$f(k,l)$ ;$\sigma_r$ 為高斯函式的標準差。
#### C++ 實現 雙邊濾波
感覺這裡寫的挺好的 [影象處理基礎(5):雙邊濾波器](https://www.cnblogs.com/wangguchangqing/p/6416401.html), 手動實現了雙邊濾波, 我們可以詳細的參考, 這裡
```cpp
// 參考來源: https://www.cnblogs.com/wangguchangqing/p/6416401.html
void myBilateralFilter(const Mat &src, Mat &dst, int ksize, double space_sigma, double color_sigma)
{
int channels = src.channels();
CV_Assert(channels == 1 || channels == 3);
double space_coeff = -0.5 / (space_sigma * space_sigma);
double color_coeff = -0.5 / (color_sigma * color_sigma);
int radius = ksize / 2;
Mat temp;
copyMakeBorder(src, temp, radius, radius, radius, radius, BorderTypes::BORDER_REFLECT);
vector _color_weight(channels * 256); // 存放差值的平方
vector _space_weight(ksize * ksize); // 空間模板係數
vector _space_ofs(ksize * ksize); // 模板視窗的座標
double *color_weight = &_color_weight[0];
double *space_weight = &_space_weight[0];
int *space_ofs = &_space_ofs[0];
for (int i = 0; i < channels * 256; i++)
color_weight[i] = exp(i * i * color_coeff);
// 生成空間模板
int maxk = 0;
for (int i = -radius; i <= radius; i++)
{
for (int j = -radius; j <= radius; j++)
{
double r = sqrt(i*i + j * j);
if (r > radius)
continue;
space_weight[maxk] = exp(r * r * space_coeff); // 存放模板係數
space_ofs[maxk++] = i * temp.step + j * channels; // 存放模板的位置,和模板係數相對應
}
}
// 濾波過程
for (int i = 0; i < src.rows; i++)
{
const uchar *sptr = temp.data + (i + radius) * temp.step + radius * channels;
uchar *dptr = dst.data + i * dst.step;
if (channels == 1)
{
for (int j = 0; j < src.cols; j++)
{
double sum = 0, wsum = 0;
int val0 = sptr[j]; // 模板中心位置的畫素
for (int k = 0; k < maxk; k++)
{
int val = sptr[j + space_ofs[k]];
double w = space_weight[k] * color_weight[abs(val - val0)]; // 模板係數 = 空間係數 * 灰度值係數
sum += val * w;
wsum += w;
}
dptr[j] = (uchar)cvRound(sum / wsum);
}
}
else if (channels == 3)
{
for (int j = 0; j < src.cols * 3; j+=3)
{
double sum_b = 0, sum_g = 0, sum_r = 0, wsum = 0;
int b0 = sptr[j];
int g0 = sptr[j + 1];
int r0 = sptr[j + 2];
for (int k = 0; k < maxk; k++)
{
const uchar *sptr_k = sptr + j + space_ofs[k];
int b = sptr_k[0];
int g = sptr_k[1];
int r = sptr_k[2];
double w = space_weight[k] * color_weight[abs(b - b0) + abs(g - g0) + abs(r - r0)];
sum_b += b * w;
sum_g += g * w;
sum_r += r * w;
wsum += w;
}
wsum = 1.0f / wsum;
b0 = cvRound(sum_b * wsum);
g0 = cvRound(sum_g * wsum);
r0 = cvRound(sum_r * wsum);
dptr[j] = (uchar)b0;
dptr[j + 1] = (uchar)g0;
dptr[j + 2] = (uchar)r0;
}
}
}
}
```
#### opencv 實現 雙邊濾波
```cpp
void bilateralFilter( InputArray _src, OutputArray _dst, int d,
double sigmaColor, double sigmaSpace,
int borderType )
```
>
