申請評分卡模型

資料的預處理與特徵構建(續)

• 課程簡介：邏輯迴歸模型的特徵需要是數值型，因此類別型變數不能直接放入模型中去，需要對其進行編碼。此外，為了獲取評分模型的穩定性，建模時需要對數值型特徵做分箱的處理。最終在帶入模型之前，我們還需要對特徵做單變數與多變數分析的工作。

目錄：

• 特徵的分箱
• WOE與特徵資訊值
• 單變數分析與多變數分析

1. 特徵的分箱

• 分箱的概念

在評分卡模型開發中，變數需要進行分箱操作才能放入模型當中。分箱操作的定義如下：

• 對於數值型變數，將其分為若干有限的幾個分段。例如，將收入分為<5K, 5K~10K, 10k~20k, >20k等
• 對於類別型變數，如果取值個數很多，將其合併為個數較少的幾個分段。例如，將省份分為{北，上，廣}，{蘇，浙，皖}，{黑，吉，遼}，{閩，粵，湘}，其他。

評分卡模型引入變數分箱操作的原因

• 評分結果需要有一定的穩定性。例如，當借款人的總體信用資質不變時，評分結果也應保持穩定。某些變數（如收入）的一點波動，不應該影響評分結果。例如，當收入按照上述劃分時，即使月收入從6k變為7k，在其他因素不變的情況下評分結果也不會發生改變。
• 類別型變數，當取值個數很多時，如果不分箱將會導致變數膨脹。例如，對於31個省級行政區（不含港澳臺），使用onehot編碼將會產生31個變數；採用啞變數編碼將會產生30個變數。

• 分箱的要求

不需要分箱的變數

對於類別型變數，如果取值個數較少，一般無需分箱

分箱結果的有序性

對於有序型變數（包括數值型和有序離散型，例如學歷），分箱要求保證有序性

分箱的平衡性

在較嚴格的情況下，分箱後的每一箱的佔比不能相差太大。一般要求佔比最小的佔，佔比不低於5%

分箱的單調性

在較嚴格的情況下，有序型變數分箱後每箱的壞樣本率要求與箱呈單調關係。

例如，將收入分為<5K, 5K~10K, 10k~20k, >20k後，壞樣本率分別是20%，15%，10%，5%。

或者，將學歷分為{低於高中}，{高中，大專}，{本科，碩士}，{博士}後，壞樣本率分別是15%，10%，5%，1%。

分箱的個數

通常要求分箱後，箱的個數不能太多，一般在7或5個以內

分箱的優點與缺點

優點：

穩定：分箱後，變數原始值在一定範圍內的波動不會影響到評分結果

缺失值處理：缺失值可以作為一個單獨的箱，或者與其他值進行合併作為一個箱

異常值處理：異常值可以和其他值合併作為一個箱

無需歸一化：從數值型變為類別型，沒有尺度的差異

缺點：

有一定的資訊丟失：數值型變數在分箱後，變為取值有限的幾個箱

需要編碼：分箱後的變數是類別型，不能直接帶入邏輯迴歸模型中，需要進行一次數值編碼

常用的分箱的方法

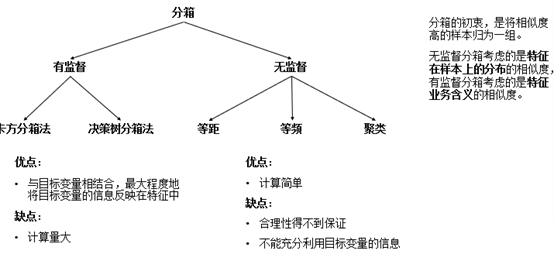
a)卡方分箱法

在有監督的分箱演算法中，卡方分箱法是常用的一種方法。它以卡方分佈和卡方值為基礎，判斷某個因素是否會影響目標變數。例如，在檢驗性別是否會影響違約概率時，可以用卡方檢驗來判斷。

卡方檢驗的無效假設H0是：觀察頻數與期望頻數沒有差別，即該因素不會影響到目標變數。基於該假設計算出χ2值，它表示觀察值與理論值之間的偏離程度。根據χ2分佈及自由度可以確定在H0假設成立的情況下獲得當前統計量及更極端情況的概率P。如果P值很小，說明觀察值與理論值偏離程度太大，應當拒絕無效假設，表示比較資料之間有顯著差異；否則就不能拒絕無效假設，尚不能認為樣本所代表的實際情況和理論假設有差別。

卡方值的計算：

• m:該因素取值個數; k：類別數
• ：因素i組中，k類別的觀察頻數
• ：原假設下的期望。

當樣本總量比較大時，χ2統計量近似服從(m-1)(k-1)個自由度的卡方分佈。

卡方檢驗的案例

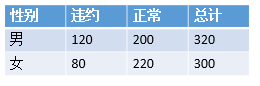
總的違約率是（120+80）/（320+300）=32.25%

如果性別與違約不相關，意味著這男性與女性的違約率是同等的，都是32.25%，則：

男性違約的期望值為320*32.25% 104，非違約的期望=320-104=216

女性違約的期望值為300*32.25% 97，非違約的期望=300-97=203

由於有隨機因素的存在，即使"性別與違約不相關"的假設成立，觀察到的男性與女性的實際違約人群也不會精確地等於104和97。卡方檢驗的思想就是衡量預測值與觀察值的差究竟有多大的概率是隨機因素引起的。如果這個概率很小， "性別與違約不相關"的假設是不成成立的，因此男、女性的違約率是不同的。此處概率需要以卡方值對應的概率來描述：

由於性別與違約狀況各有2種類別，卡方檢驗的自由度為（2-1）（2-1）=1，=8.05 對應的p值=0.005,因此性別在違約行為上有顯著地影響。

卡方(ChiMerge)分箱法（續）

ChiMerge法採取自底向上不斷合併的方法完成分箱操作。在每一步的合併過程中，依靠最小的卡方值來尋找最優的合併項。其核心思想是，如果某兩個區間可以被合併，那麼這兩個區間的壞樣本需要有最接近的分佈，進而意味著兩個區間的卡方值是最小的。於是ChiMerge的步驟如下：

1. 將數值變數排序後分成區間較多的若干組，設為
2. 計算合併後的卡方值，合併後的卡方值，直至合併後的卡方值
3. 找出上一步所有合併後的卡方值中最小的一個，假設為,將其合併形成新的
4. 不斷重複2和3，直至滿足終止條件

通用的ChiMerge的終止條件是：

1. 某次合併後，最小的卡方值的p值超過0.9（或0.95，0.99等），或者
2. 某側合併後，總的未合併的區間數達到指定的數目（例如5，10，15等）

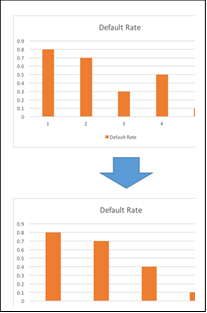
壞樣本率非單調情形下的分箱合併

如前所述，當卡方分箱法完成分箱後，每一箱的壞樣本率不一定滿足單調的要求，此時需要做進一步的合併。此時有2種方案：

1. 利用卡方分箱法縮減分箱數目。例如，當前分為5箱時出現壞樣本率非單調情形，可以在卡方分箱法中設定分箱數為4，檢驗分箱數目為4時候的單調性。如果滿足，即停止分箱；如不滿足，可進一步地縮減分箱數目。分箱數目最小為2，因為只有兩箱的情況下，單調性的存在性失去意義了。
2. 對於當前不滿足單調性的箱，可以與之前或之後的箱進行合併。如上一頁圖中，第3箱的的壞樣本率低於前後兩箱，於是需要合併。選擇與之前或者之後的箱進行合併，可以依據以下原則：
3. 合併之後，非單調的程度減輕。例如將第3箱和第4箱進行合併後，整體的單調性得到保證，於是執行該方案
4. 如果兩種方案都可以減輕非單調性，則可以選擇"較優"的一種。一般來講，可以從2點考量是否"較優"。假設合併2、3箱優於合併3、4箱，因為

• 合併2、3箱後的卡方值低於合併3、4箱後的卡方值，或者
• 合併2、3箱後，所有箱的佔比比合並3、4箱後的佔比更加平衡。

判斷分箱後的分佈均勻性

• 假設將原變數分為m箱，每箱的佔比分別是.
• 可以用以下公式衡量佔比的均勻性：
•  
• 由施瓦茨不等式可以知道，當時， 最小，

  等於。當中有一個為1其餘為0時， 最大，等於1.於是可以看出，Balance越小表明越均勻。

帶有特殊值的分箱

在實際業務工作中，一些正常的觀測值之外有時會有一些特殊值的存在，例如缺失。從之前的分析可以知道，本次案例的資料中部分變數含有一些缺失值。在評分卡模型中，對於缺失值通常我們將其看成一種特殊的值。連續型變數的分箱工作需要預先將這些特殊值排除在外，即特殊值不參與分箱。

當連續型變數存在特殊值時，需要將特殊值看成單獨的一箱，其餘正常值參與分箱，且分箱個數為預設個數減去特殊值的個數。這裡需要注意：

• 由於特殊值無法和其他數值進行比較，故檢驗壞樣本率的單調性時，不考慮特殊值的壞樣本率
• 當特殊值的佔比很小（例如低於5%），可以考慮將特殊值與正常值中的一箱進行合併，且通常與最小的一箱或者最大的一箱進行合併

類別型（無序）變數的分箱

上述介紹的ChiMerge分箱法是針對數值型變數，例如收入、年齡等。分箱過程要保持原變數的有序性。對於類別型變數，如果是無序且取值個數較大，此時進行ChiMerge分箱之前需要先進行一次數值編碼，用數字代替原來的類別型值。常用的數值編碼是該數值對應的平均壞樣本率。

例如，在評分模型裡省份是一個常用的變數。在31個省級行政區（不含港澳臺）中，我們用每個省在樣本里的壞樣本率代替原先的省級行政區。在這樣的轉換之下，類別型變數就轉換成數值型變數。進而可以使用ChiMerge分箱法進行分箱操作。分箱後的省份可能是{北上廣深}，{蘇浙魯閩}，{其他}等。

類別型（有序）變數的分箱

對於有序的類別型變數，例如學歷={小學，初中，高中，大專，本科，碩士，博士}，先將該變數進行排序，然後依然可以按照數值型變數的ChiMerge分箱法來進行分箱。"學歷"這一邊量最終的分箱結果可能是{小學，初中，高中}，{大專，本科}，{碩士，博士}

ChiMerge分箱法的優點與缺點

1. WOE與特徵資訊值

WOE編碼

編碼操作是一種用數值代替非數值的操作，目的是為了讓模型能夠對其進行數學運算。例如，可以用3組0~255之間的整數來對顏色進行編碼。在評分卡模型開發中，完成變數的分箱後所有的變數都變成了組別。此時需要對其進行編碼才能下一步的建模。評分卡模型裡常用WOE（Weight of Evidence）的形式進行分箱後的編碼。其計算公式如下：

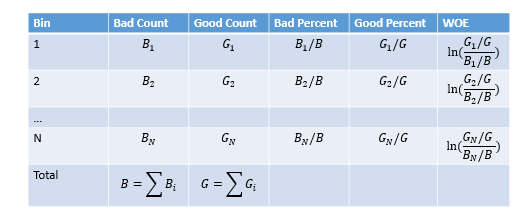
WOE編碼的含義

注意到WOE公式

我們有：

1. WOE的符號性質：

即如果某箱的WOE是正的，表明該箱的壞樣本率低於整個樣本的平均壞樣本率，相對更加容易出現好樣本

1. WOE的單調性質:

即WOE的單調性與壞樣本率的單調性相反。

使用WOE編碼的注意點

• 從WOE的計算公式可以看出，要使得某一箱的有意義，則與必須為大於0的正數。這也意味著在上一步的分箱操作中，每一箱都必須同時包含好壞樣本。
• 上式的對數計算中，好、壞樣本的佔比分別在分子和分母上。也可以好、壞樣本的佔比分別在分母和分子上，但是要求某一個模型裡，所有變數的處理方式是一致的。同時，WOE的計算方式對後續邏輯迴歸模型的變數的符號是有一定的要求的。

WOE編碼的優點與缺點

WOE編碼的優點

提高模型的效能：以每一箱中的相對全體的log odds的超出作為編碼依據，能夠提高模型的預測精度

統一變數的尺度：經驗上來看，WOE編碼後的取值範圍一般介意-4與4之間

分層抽樣中的WOE不變性：如果建模需要對好壞樣本進行分層抽樣，則抽樣後計算的WOE與未抽樣計算的WOE是一致的

WOE編碼的缺點

要求每箱中同時包含好壞樣本：已在之前有過說明

對多類別標籤無效：如果目標變數取值個數超過2個，分箱後的WOE是無法計算的

特徵資訊值（IV）

在評分卡模型中，衡量變數重要性的工作是一項必要的工作。在特徵工程的初期我們往往能夠衍生出數量較多的變數，但是並不能保證這些變數對於模型開發來說都很重要。通過衡量變數重要性，能夠讓我們從中挑選出相對更加重要的變數，為後續的分析提供降維的能力。此處我們通過計算特徵資訊值（Information Value）來衡量其重要性。其計算公式如下：

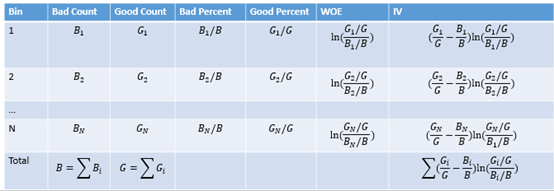
從上式的計算可以看出，某變數的IV是該變數每個箱的WOE的加權，權重是。如前所述，WOE的計算也可以是。則此時權重也影響修正為。關於IV，我們有：

非負性：如果,則, 且, 進而有, 從而,於是IV>0.

權重性：WOE反映的是每箱中好壞比相對全體樣本好壞比的超出（excess），而IV反映的是在該箱體量的意義下，這種超出的顯著性。例如，某一箱的好、壞各自佔了2%和1%，另一箱中的好、壞各自佔了20%和10%。從WOE的角度看， 二者是一致的，都是ln(2)。但是前者的體量較少而後者的體量較大，分別是（2%-1%）=1%與（20%-10%）=10%。所以後者的顯著性更強一些。

關於IV，我們需要注意幾點：

1. IV衡量的是特徵總體的重要性，而非每一箱的重要性。IV值越大，則表明該變數的重要程度越高。但是IV的值不宜太大，否則有可能有過擬合的風險。
2. 與WOE一樣，IV也要求每一箱中同時包含好壞樣本
3. IV不僅受到變數重要性的影響，同時也與分箱方式有關。通常來講，一個變數分箱的粒度越細，則IV會升高。所以需要注意到分箱的合理性。若干個變數分箱的個數差異不大時，才能比較IV。

3. 單變數分析與多變數分析

• 單變數分析（Single Factor Analysis）

完成變數分箱、WOE編碼與IV計算後，我們需要做單變數分析。一般而言從兩個角度進行分析：

1. 變數的重要性。變數的重要性可以從IV值的判斷出發。不同的IV值反映出變數不同程度的重要性。一般而言，IV的選擇如下：

但是當IV異常高，例如超過1時，需要注意此時變數的分箱方式可能是不穩定的。

1. 變數分佈的穩定性。合適的變數，各箱的佔比不會很懸殊。如果某變數有一箱的佔比遠低於其他箱，則該變數的穩定性也較弱。

單變數分析是從重要性及分佈的穩定性兩個角度來考慮。通常先選擇IV高於閾值（如0.2）的變數，再挑選出分箱較均勻的變數。

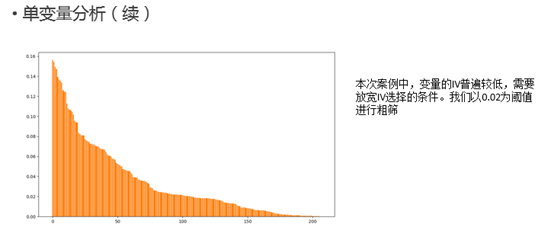
多變數分析（Multi Factors Analysis）

完成單變數分析後，我們還需要對變數的整體性做把控，利用多變數分析的技術進一步縮減變數規模，形成全域性更優的變數體系。多變數分析從以下兩個角度分析變數的特性並完成挑選工作:

• 變數間的兩兩線性相關性
• 變數間的多重共線性

變數間不允許存在太強的兩兩線性相關性。主要原因是：

• 若變數和變數的兩兩線性相關性較強，說明這兩個變數間存在一定的資訊冗餘。同時保留在模型裡，即無必要，同時也增加了模型開發、部署與維護的負擔
• 較強的線性相關性甚至會影響迴歸模型的引數估計。在迴歸模型的引數估計中，當兩個變數間存在較強的線性相關性時，引數的估計會有較大的偏差

多變數分析（續）

完成變數間的兩兩線性相關性檢驗後，我們還需要檢驗是否存在多重共線性（multicolinearity）。多重共線性是指，一組變數中，某一個變數與其他變數的線性組合存在較強的線性相關性。同樣地，存在較強的多重共線性意味著存在資訊冗餘，且對模型的引數估計產生影響。多重共線性通常用方差膨脹因子（VIF）來衡量，其計算方式如下：

其中是對的線性迴歸的決定係數。

一般而言，我們用10來衡量是否存在多重共線性。對於VIF>10，可以認為變數間存在多重共線性。此時，需要逐步從剔除一個變數，剩餘的變數與計算VIF。如果發現當剔除後剩餘變數對的VIF低於10，則從與中剔除IV較低的一個。如果每次剔除一個變數還不能降低VIF，則每次剔除2個變數，直至變數間不存在多重共線性