機器學習——十大資料探勘之一的決策樹CART演算法
阿新 • • 發佈:2020-06-06
本文始發於個人公眾號:TechFlow,原創不易,求個關注
今天是**機器學習專題**的第23篇文章,我們今天分享的內容是十大資料探勘演算法之一的CART演算法。 CART演算法全稱是**Classification and regression tree**,也就是分類迴歸樹的意思。和之前介紹的ID3和C4.5一樣,CART演算法同樣是決策樹模型的一種經典的實現。決策樹這個模型一共有三種實現方式,前面我們已經介紹了ID3和C4.5兩種,今天剛好補齊這最後一種。
## 演算法特點
CART稱為分類迴歸樹,從名字上我們也看得出來,它既能支援分類又可以支援迴歸。的確如此,決策樹的確支援迴歸操作,但是我們一般不會用決策樹來進行迴歸。這裡面的原因很多,除了樹模型擬合能力有限效果不一定好之外,還與特徵的模式有關係,樹迴歸模型受到特徵的影響非常大。這個部分我們不做太多深入,之後會在迴歸樹的文章當中詳細探討。 正因為迴歸樹模型效果表現都不太理想,所以CART演算法實現決策樹**基本都是用來做分類問題**。那麼在分類問題上,它與之前的ID3演算法和C4.5演算法又有什麼不同呢? 主要細究起來大約有兩點,第一點是CART演算法使用Gini指數而不是資訊增益來作為劃分子樹的依據,第二點是CART演算法每次在劃分資料的時候,固定將整份資料拆分成兩個部分,而不是多個部分。由於CART每次將資料拆分成兩個部分,所以**它對於拆分的次數沒有限制**,而C4.5演算法對特徵進行了限制,限制了每個特徵最多隻能使用一次。因為這一點,同樣CART對於剪枝的要求更高,因為不剪枝的話很有可能導致樹過度膨脹,以至於過擬合。
## Gini指數
在ID3和C4.5演算法當中,在拆分資料的時候用的是資訊增益和資訊增益比,這兩者都是基於資訊熵模型。資訊熵模型本身並沒有問題,也是非常常用的模型。唯一的問題是,在計算熵的時候需要涉及到log運算,相比於四則運算來說,**計算log要多耗時很多**。 Gini指數本質上也是基於資訊熵模型,只是我們在計算的時候做了一些轉化,從而避免了使用log進行計算,加速了計算的過程。兩者的內在邏輯是一樣的。那怎麼實現的加速計算呢?這裡用到了高等數學當中的**泰勒展開**,我們將log運算通過泰勒公式展開,轉化成多項式的計算,從而加速資訊熵的計算。 我們來做一個簡單的推導: $$ \begin{aligned} \ln(x) \approx \ln(x_0) + (x-x_0)\ln'(x_0) + o(x) \end{aligned} $$ 我們把$x_0 =1$代入,可以得到:$\ln(x)=x - 1 + o(x)$,其中o(x)是關於x的高階無窮小。我們把這個式子套入資訊熵的公式當中: $$ \begin{aligned} H(x) &= -\sum_{i=1}^k p_i\ln p_i \\ &\approx \sum_{i=1}^k p_i(1-p_i) \end{aligned} $$ 這個就是Gini指數的計算公式,這裡的**pi表示類別i的概率**,其實就是類別i的樣本佔全體樣本的比例。那麼上面的式子也可以看成是從資料集當中抽取兩條樣本,它們類別不一致的概率。 因此**Gini指數越小,說明資料集越集中**,也就是純度越高。它的概念等價於資訊熵,熵越小說明資訊越集中,兩者的概念是非常近似的。所以當我們使用Gini指數來作為劃分依據的時候,選擇的是切分之後Gini指數儘量小的切分方法,而不是儘量大的。 從上面的公式當中,我們可以發現相比於資訊熵的log運算,Gini指數只需要簡單地計算比例和基礎運算就可以得到結果了,顯然運算速度要快得多。並且由於是通過泰勒展開逼近的,整體的效能也並不差,我們可以看下下面這張經典的圖感受一下: 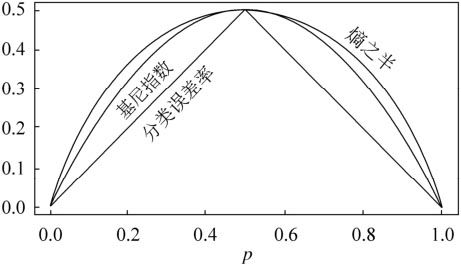 從上圖當中可以看出來,Gini指數和資訊熵的效果非常接近,一樣可以非常好地反應資料劃分的純度。
## 拆分與剪枝
剛才我們介紹CART演算法特性的時候提到過,CART演算法**每次拆分資料都是二分的**,這點和C4.5處理連續性特徵的邏輯很像。但有兩點不同,第一點是CART對於離散型和連續性特徵都如此操作,另外一點是,CART演算法當中一個特徵可以重複使用。 舉個例子,在之前的演算法當中,比如說西瓜的直徑是一個特徵。那麼當我們判斷過西瓜的直徑小於10cm之後,西瓜的直徑這個特徵就會從資料當中移除,之後再也不會用到。但是在CART演算法當中不是如此,比如當我們先後根據西瓜的直徑以及西瓜是否有藤這兩個特徵對資料進行拆分之後,對於ID3和C4.5演算法來說,西瓜的直徑這個特徵已經不可以再用來作為劃分的依據了,但是CART演算法當中可以,我們仍然可以繼續使用之前已經用過的特徵。 我們用一張圖來展示,大概是下面這個樣子:  我們觀察一下最左側的子樹,直徑這個特徵出現了不止一次,這其實是很合理的。然而這也會有一個問題,就是由於沒有了特徵只能用一次這個限制,這樣**會導致這棵樹無限膨脹**,尤其是在連續性特徵很多的情況下,很容易陷入過擬合。為了放置過擬合,增加模型的泛化能力,我們需要對生成的這棵樹進行剪枝。 剪枝的方案主流的有兩種,**一種是預剪枝,一種是後剪枝**。所謂的預剪枝,即是在生成樹的時候就對樹的生長進行限制,防止過度擬合。而後剪枝則是在樹已經生成之後,對過擬合的部分進行修剪。其中預剪枝比較容易理解,比如我們可以限制決策樹在訓練的時候每個節點的資料只有在達到一定數量的情況下才會進行分裂,否則就成為葉子節點保留。或者我們可以限制資料的比例,當節點中某個類別的佔比超過閾值的時候,也可以停止生長。 後剪枝相對來說複雜一些,需要我們在生成樹之後通過一些機制尋找可以剪枝的部分,對整棵樹進行修剪。比如在CART演算法當中常用的剪枝策略是CCP,它的英文全寫是Cost-Complexity Pruning,即**代價複雜度剪枝**。這個策略設計了一個指標來衡量一棵子樹的複雜度代價,我們可以對這個代價設定閾值來進行剪枝。 這個策略的精髓在於下面這個式子: $$c = \frac{R(t) - R(T_t)}{|N_t| - 1}$$ 這個式子當中的c就是指的剪枝帶來的代價,t代表剪枝之後的子樹,$T_t$表示剪枝之前的子樹。R(t)表示剪枝之後的**誤差代價**,$R(T_t)$表示剪枝之前的誤差代價。其中誤差代價的定義是:$R(t) = r(t) * p(t)$,r(t)是節點t的誤差率,p(t)是t上資料佔所有資料的比例。 我們來看個例子:  假設我們知道所有資料一共有100條,那麼我們代入公式算一下,可以得到$R(t) = r(t) * p(t) = \frac{11}{23} * \frac{23}{100} = \frac{11}{100}$ 子樹的誤差代價是: $$R(T_t) = \sum R(i)=(\frac{2}{6}*\frac{6}{100})+ (\frac{0}{3}*\frac{3}{100}) + (\frac{2}{8}*\frac{8}{100})=\frac{4}{100}$$ 所以可以得到$c=\frac{11/100 - 4/100}{3 - 1}=\frac{7}{200}$ **c越大說明剪枝帶來的偏差越大,也就是說越不能剪**,相反c很小說明偏差不大,可以減掉。我們只需要設定閾值,然後計算每一棵子樹的c來判斷是否能夠剪枝即可。
## 程式碼實現
我們之前已經實現過了C4.5演算法,再來實現CART可以說是非常簡單了,因為它相比於C4.5還少了離散型別這種情況,可以全部當做是連續型型別來處理。 我們**只需要把之前的資訊增益比改成Gini指數**即可: ```python from collections import Counter def gini_index(dataset): dataset = np.array(dataset) n = dataset.shape[0] if n == 0: return 0 # sigma p(1-p) = 1 - sigma p^2 counter = Counter(dataset[:, -1]) ret = 1.0 for k, v in counter.items(): ret -= (v / n) ** 2 return ret def split_gini(dataset, idx, threshold): left, right = [], [] n = dataset.shape[0] # 根據閾值拆分,拆分之後計算新的Gini指數 for data in dataset: if data[idx] < threshold: left.append(data) else: right.append(data) left, right = np.array(left), np.array(right) # 拆分成兩半之後,乘上所佔的比例 return left.shape[0] / n * gini_index(left) + right.shape[0] / n * gini_index(right) ``` 然後選擇拆分的函式稍微調整一下,因為Gini指數越小越好,之前的資訊增益和資訊增益比都是越大越好。程式碼的框架基本上也沒有變動,只是做了一些微調: ```python def choose_feature_to_split(dataset): n = len(dataset[0])-1 m = len(dataset) # 記錄最佳Gini,特徵和閾值 bestGini = 1.0 feature = -1 thred = None for i in range(n): threds = get_thresholds(dataset, i) for t in threds: # 遍歷所有的閾值,計算每個閾值的資訊增益比 ratio = split_gini(dataset, i, t) if ratio < bestGini: bestGini, feature, thred = ratio, i, t return feature, thred ``` 建樹和預測的部分都和之前C4.5演算法基本一致,只需要**去掉離散型別的判斷**即可,大家可以參考一下之前文章當中的程式碼。
## 總結
到這裡,我們關於決策樹模型的內容就算是結束了,我們從基本的決策樹原理,再到ID3、C4.5以及CART演算法,都已經囊括了。這些知識儲備**足以應對面試當中關於決策樹模型的問題了**。 雖然在實際的生產過程當中,我們已經用不到決策樹了,還不是基本用不到,幾乎是完全用不到。但是它的思想非常重要,是後續很多模型的基礎,比如隨機森林、GBDT等模型,都是在決策樹的基礎上建立起來的。所以我們深入理解決策樹的原理對於我們後續的進階學習非常重要。 最後, 我把完整的程式碼發在了paste.ubuntu上,需要的同學可以在公眾號後臺回覆“**決策樹**”獲取。 如果喜歡本文,可以的話,請**點個關注**,給我一點鼓勵,也方便獲取更多文章。  \approx \ln(x_0) + (x-x_0)\ln'(x_0) + o(x) \end{aligned} $$ 我們把$x_0 =1$代入,可以得到:$\ln(x)=x - 1 + o(x)$,其中o(x)是關於x的高階無窮小。我們把這個式子套入資訊熵的公式當中: $$ \begin{aligned} H(x) &= -\sum_{i=1}^k p_i\ln p_i \\ &\approx \sum_{i=1}^k p_i(1-p_i) \end{aligned} $$ 這個就是Gini指數的計算公式,這裡的**pi表示類別i的概率**,其實就是類別i的樣本佔全體樣本的比例。那麼上面的式子也可以看成是從資料集當中抽取兩條樣本,它們類別不一致的概率。 因此**Gini指數越小,說明資料集越集中**,也就是純度越高。它的概念等價於資訊熵,熵越小說明資訊越集中,兩者的概念是非常近似的。所以當我們使用Gini指數來作為劃分依據的時候,選擇的是切分之後Gini指數儘量小的切分方法,而不是儘量大的。 從上面的公式當中,我們可以發現相比於資訊熵的log運算,Gini指數只需要簡單地計算比例和基礎運算就可以得到結果了,顯然運算速度要快得多。並且由於是通過泰勒展開逼近的,整體的效能也並不差,我們可以看下下面這張經典的圖感受一下:  從上圖當中可以看出來,Gini指數和資訊熵的效果非常接近,一樣可以非常好地反應資料劃分的純度。
## 拆分與剪枝
剛才我們介紹CART演算法特性的時候提到過,CART演算法**每次拆分資料都是二分的**,這點和C4.5處理連續性特徵的邏輯很像。但有兩點不同,第一點是CART對於離散型和連續性特徵都如此操作,另外一點是,CART演算法當中一個特徵可以重複使用。 舉個例子,在之前的演算法當中,比如說西瓜的直徑是一個特徵。那麼當我們判斷過西瓜的直徑小於10cm之後,西瓜的直徑這個特徵就會從資料當中移除,之後再也不會用到。但是在CART演算法當中不是如此,比如當我們先後根據西瓜的直徑以及西瓜是否有藤這兩個特徵對資料進行拆分之後,對於ID3和C4.5演算法來說,西瓜的直徑這個特徵已經不可以再用來作為劃分的依據了,但是CART演算法當中可以,我們仍然可以繼續使用之前已經用過的特徵。 我們用一張圖來展示,大概是下面這個樣子:  我們觀察一下最左側的子樹,直徑這個特徵出現了不止一次,這其實是很合理的。然而這也會有一個問題,就是由於沒有了特徵只能用一次這個限制,這樣**會導致這棵樹無限膨脹**,尤其是在連續性特徵很多的情況下,很容易陷入過擬合。為了放置過擬合,增加模型的泛化能力,我們需要對生成的這棵樹進行剪枝。 剪枝的方案主流的有兩種,**一種是預剪枝,一種是後剪枝**。所謂的預剪枝,即是在生成樹的時候就對樹的生長進行限制,防止過度擬合。而後剪枝則是在樹已經生成之後,對過擬合的部分進行修剪。其中預剪枝比較容易理解,比如我們可以限制決策樹在訓練的時候每個節點的資料只有在達到一定數量的情況下才會進行分裂,否則就成為葉子節點保留。或者我們可以限制資料的比例,當節點中某個類別的佔比超過閾值的時候,也可以停止生長。 後剪枝相對來說複雜一些,需要我們在生成樹之後通過一些機制尋找可以剪枝的部分,對整棵樹進行修剪。比如在CART演算法當中常用的剪枝策略是CCP,它的英文全寫是Cost-Complexity Pruning,即**代價複雜度剪枝**。這個策略設計了一個指標來衡量一棵子樹的複雜度代價,我們可以對這個代價設定閾值來進行剪枝。 這個策略的精髓在於下面這個式子: $$c = \frac{R(t) - R(T_t)}{|N_t| - 1}$$ 這個式子當中的c就是指的剪枝帶來的代價,t代表剪枝之後的子樹,$T_t$表示剪枝之前的子樹。R(t)表示剪枝之後的**誤差代價**,$R(T_t)$表示剪枝之前的誤差代價。其中誤差代價的定義是:$R(t) = r(t) * p(t)$,r(t)是節點t的誤差率,p(t)是t上資料佔所有資料的比例。 我們來看個例子:  假設我們知道所有資料一共有100條,那麼我們代入公式算一下,可以得到$R(t) = r(t) * p(t) = \frac{11}{23} * \frac{23}{100} = \frac{11}{100}$ 子樹的誤差代價是: $$R(T_t) = \sum R(i)=(\frac{2}{6}*\frac{6}{100})+ (\frac{0}{3}*\frac{3}{100}) + (\frac{2}{8}*\frac{8}{100})=\frac{4}{100}$$ 所以可以得到$c=\frac{11/100 - 4/100}{3 - 1}=\frac{7}{200}$ **c越大說明剪枝帶來的偏差越大,也就是說越不能剪**,相反c很小說明偏差不大,可以減掉。我們只需要設定閾值,然後計算每一棵子樹的c來判斷是否能夠剪枝即可。
## 程式碼實現
我們之前已經實現過了C4.5演算法,再來實現CART可以說是非常簡單了,因為它相比於C4.5還少了離散型別這種情況,可以全部當做是連續型型別來處理。 我們**只需要把之前的資訊增益比改成Gini指數**即可: ```python from collections import Counter def gini_index(dataset): dataset = np.array(dataset) n = dataset.shape[0] if n == 0: return 0 # sigma p(1-p) = 1 - sigma p^2 counter = Counter(dataset[:, -1]) ret = 1.0 for k, v in counter.items(): ret -= (v / n) ** 2 return ret def split_gini(dataset, idx, threshold): left, right = [], [] n = dataset.shape[0] # 根據閾值拆分,拆分之後計算新的Gini指數 for data in dataset: if data[idx] < threshold: left.append(data) else: right.append(data) left, right = np.array(left), np.array(right) # 拆分成兩半之後,乘上所佔的比例 return left.shape[0] / n * gini_index(left) + right.shape[0] / n * gini_index(right) ``` 然後選擇拆分的函式稍微調整一下,因為Gini指數越小越好,之前的資訊增益和資訊增益比都是越大越好。程式碼的框架基本上也沒有變動,只是做了一些微調: ```python def choose_feature_to_split(dataset): n = len(dataset[0])-1 m = len(dataset) # 記錄最佳Gini,特徵和閾值 bestGini = 1.0 feature = -1 thred = None for i in range(n): threds = get_thresholds(dataset, i) for t in threds: # 遍歷所有的閾值,計算每個閾值的資訊增益比 ratio = split_gini(dataset, i, t) if ratio < bestGini: bestGini, feature, thred = ratio, i, t return feature, thred ``` 建樹和預測的部分都和之前C4.5演算法基本一致,只需要**去掉離散型別的判斷**即可,大家可以參考一下之前文章當中的程式碼。
## 總結
到這裡,我們關於決策樹模型的內容就算是結束了,我們從基本的決策樹原理,再到ID3、C4.5以及CART演算法,都已經囊括了。這些知識儲備**足以應對面試當中關於決策樹模型的問題了**。 雖然在實際的生產過程當中,我們已經用不到決策樹了,還不是基本用不到,幾乎是完全用不到。但是它的思想非常重要,是後續很多模型的基礎,比如隨機森林、GBDT等模型,都是在決策樹的基礎上建立起來的。所以我們深入理解決策樹的原理對於我們後續的進階學習非常重要。 最後, 我把完整的程式碼發在了paste.ubuntu上,需要的同學可以在公眾號後臺回覆“**決策樹**”獲取。 如果喜歡本文,可以的話,請**點個關注**,給我一點鼓勵,也方便獲取更多文章。 