# Harris角點檢測 ## 思想 為什麼要檢測角點呢？因為角點的特徵比較明顯。進行角點檢測的樸素思想是利用影象梯度，也就是根據影象強度的變化來尋找角點。如圖所示 這裡舉了個例子，給定一個小的區域（Patch），當這個小區域在不同位置滑動的時候，所呈現出來的一些特性是不同的，根據圖示，有三個方面。 - Flat，平的地方，在任何方向，梯度都沒什麼變化。 - Edge，邊的地方，當沿著邊方向的時候，梯度沒什麼變化。 - Corner，角的地方，沿著任何方向，梯度都有變化。 ## Error Function $$ E(u,v)=\sum_{x,y}{w(x,y)[I(x+u,y+v)-I(x,y)]^2} $$ - $x,y$是相對於一個小patch來說的，例如一個5*5的區域 - $(u,v)$是一個很小的移動量 - $w(x,y)$是windows function，也就是對於每個點的權重，例如想讓中心的點權重高，可以用高斯核，一般就是全1或者高斯。 - $I(x,y)$就代表影象在$(x,y)$的強度值。 - 後面做差其實就是類似求梯度一樣 根據之前的討論，在一個patch裡，如果有角點的存在，各個方向的梯度值都很大，於是乎，我們的目標是讓$E(u,v)$儘可能的大。 因為$(u,v)$的值很小，所以我們可以利用二元函式的泰勒展開，來近似計算。 二元函式的泰勒展開，當然扔掉了一些項。 $$ f(x+u,y+v) \approx f(x,y)+uf_x(x,y)+vf_y(x,y) $$ 那麼我們對Error function中的關鍵部分進行展開 $$ \begin{aligned} [I(x+u,y+v)-I(x,y)]^2 &\approx [I(x,y)+uI_x+vI_y-I(x,y)]\\ &=(uI_x+vI_y)^2\\ &=[u,v] \begin{bmatrix} I_x^2 &I_xI_y\\ I_xI_y&I_y^2 \end{bmatrix} \begin{bmatrix} u\\v \end{bmatrix} \end{aligned} $$ 所以Error Function可以近似為 $$ E(u,v)\approx [u,v]M\begin{bmatrix} u\\v \end{bmatrix} $$ $$ M= \sum_{x,y}{w(x,y) \begin{bmatrix} I_x^2 &I_xI_y\\ I_xI_y&I_y^2 \end{bmatrix} } $$ 這就涉及到線性代數裡的二次型問題了。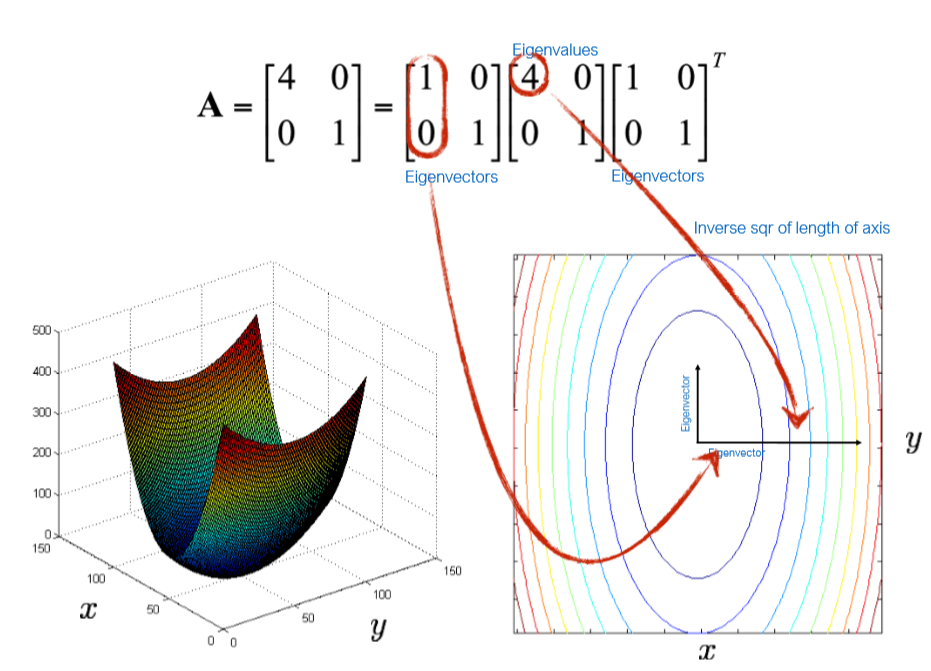 ## 簡單的二次型 例如 $f(x,y) = x^2+y^2$的可以寫作矩陣的形式 $$ [x,y]\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix} $$ 由中間這個矩陣來決定這個二次型的形狀，因為我們研究的二次型只有兩個變數，所以可以視覺化來理解如下圖所示。對形狀矩陣可以進行特徵分解，分為中間的對角陣（對角線都是特徵值）兩邊是特徵向量。特徵向量代表了橢圓切片的長短軸的方向，而特徵值平方根的倒數代表了軸的長短。至於為什麼分解完會和橢圓對應，線性代數書上會有。 這樣就把Error Function給可視化了，有了幾何含義，更加直觀了。 - Flat的時候，$(u,v)$往哪個方向變化都不大，反應在幾何上，應該是一個較為平坦的面 - Edge的時候，$(u,v)$往某個方向變化大，反應在幾何上，應該是某個方向翹起。 - Corner的時候，$(u,v)$往大部分方向變化都大，反應在幾何上，應該是大部分方向都翹起。 如圖所示 我們可以通過兩個特徵值之間的大小關係，以及他們自身的關係來作為評估的依據。  當兩個特徵值都很大，且差不多時，意味著角點。 ## 角點響應的度量 以上分析了，要兩個特徵值都很大，且同時大，那怎麼來度量？於是乎在最原始的論文裡，這樣定義了響應函式，並且對不同的$\lambda$有以下的響應圖 $$ R = det(M)-k(trace(M))^2\\ det(M) = \lambda_1\lambda_2\\ trace(M) = \lambda_1+\lambda_2 $$ $k$一般在是0.04-0.06  如圖所示，黃色的線是等值線，代表$R$的值都相同，左上角是$(0,0)$點，往右下角去$R$的值越大，代表角點的響應越高，圖中畫了個綠線，右側的R值基本可以判斷為是角點了。另外還有一些別的響應函式，基本大同小異吧。 ## 演算法 所以現在經過以上的分析，總結一下角點檢測的演算法步驟。 1. 計算整個影象的梯度值$I_x,I_y$ 2. 對於每個畫素的$I_{x^2}=I_xI_x,I_{y^2}=I_yI_y,I_{xy}=I_xI_y$ 3. 計算每一個畫素視窗的和，意思就是對於一個畫素，定義一個領域例如5\*5，就和之前提及的那樣，然後計算這個鄰域裡面所有第二步計算出來的值的和。$S_{x^2}=G_{\sigma}*I_{x^2},S_{y^2}=G_{\sigma}*I_{y^2},S_{xy}=G_{\sigma}*I_{xy}$ 4. 對於每個點$(x,y)$，定義矩陣$\begin{bmatrix}S_{x^2}&S_{xy}\\S_{xy}&S_{y^2}\end{bmatrix}$ 5. 對於每個點，計算響應值$R=Det(H)-k(Trace(H))^2$ 6. 對$R$設定閾值，並且計算非極大值抑制（nonmax suppression, NMS），這個的意思應該就是比如5\*5的鄰域內有好幾個點通過了閾值的篩選，那麼選擇最大的那個，抑制其他的點。 ## 一些特性 - Harris角點響應具有旋轉不變性，因為旋轉不會改變特徵值的大小。 - Harris角點響應對強度變化具有一定的不變性，縮放或者平移。因為經過縮放或者平移，最大值還是最大值，但是閾值可能要改改。 - Harris角點響應不對尺度有不變性，改變尺度可能會改變檢測的結果。可能在某一尺度下檢測出為角點，而另一尺度檢測出為邊緣。 # 參考 - [1]CSE486 PSU http://www.cse.psu.edu/~rtc12/CSE486/ - [2]16-385 CMU 5http://www.cs.cmu.edu