~~寫在前面：圖論題的除錯真感人~~ 讓我們進入正題 ##最短路是啥 emmm 顧名思義最短路就是求一個點到另外一個點的最小距離 一般來說最短路分為：單源最短路和多源最短路 單源最短路就是求一個源點到另外多個點的最短距離 而多源最短路就是求多個點到其他點的最短距離 演算法一般有： * floyd（多源 O($n^3$)） * dijkstra（單源 O($n^2$) 可用堆優化到O($n*log_n$)） * Bellman-Ford(單源 O($nE$)) * SPFA(單源 O(nE 但是比BF強)) 具體的優劣以及使用範圍我們會在下面具體講解
##floyd 演算法 * 適用範圍 ： 多源最短路 可處理負權 但是不能處理負環 執行一次可求得任意兩點間最短路 * floyd演算法其實很好理解 也很好寫（畢竟 O($n^3$)）~~有的時候可以將其當作dp理解~~ * 先來想這樣一個問題 ： 現在你在老家（B地）自由自在的玩耍著 突然有人告訴你去A地能給你分物件 （咳咳） 然後你就屁顛屁顛的跑去了A地 但是有好多人都要去A地 你希望可以最快到達A地（也就是路徑最短） * 顯然你可以直接坐車從B地直接趕往A地 但是這樣一定是最短的嗎？ 然並卵 畢竟路上你要走山路十八彎 而這時C地出現在你的面前 從B直接到A要走1000km（反正很遠很遠） 但是從B到C只需要 1 km，從C到B呢也只需要 1 km（反正很短很短）那你肯定會先到C 再到B吧 * 這就是我們的核心思路了 揪黑板！！ 如果我們已知並記錄了從i到j的最短路徑 而如果將k作為中轉點可以使得我們的最短路徑更短 那我們就更新i到j的最短路徑 （其他演算法也會用到這個思想，即下面的鬆弛操作） ###核心程式碼實現： ```cpp for(int k=1;k<=n;++k)//列舉中轉點 for(int i=1;i<=n;++i)//列舉邊的起點 for(int j=1;j<=n;++j)//列舉邊的終點 if(a[i][j]>a[i][k]+a[k][j])//鬆弛操作（即利用第三個點來判斷是否可以更新目標兩個點的最短距離） a[i][j]=a[i][k]+a[k][j];//a[i][j]是從i到j的最小值 ``` 關於k為什麼要列舉在第一層迴圈: 剛才已經說過floyd類似於dp，而k就是dp的階段（dp的階段顯然要列舉在第一層的），其實a本來是三維a[k][i][j]表示只經過前k個點從i到j的最短路，而可以將第一維的k捨去（like揹包） 所以就成了現在的樣子啦
## dijkstra 演算法 * 適用範圍：單源最短路 不能處理帶有負權邊的圖 需要指定起點s * dij是求最短樓最常用的方法也是最經典的： 然後維護一個集合S用於存放已經知道對於源點s的最短距離的點 另外一個集合U用於維護還不知道對於源點s的最短距離的點（但是可以知道當前不完全狀態下的最短距離） * 初始時 S中只有s自己 距離自己的距離是0 而其他點距離s的距離都初始化為正無窮 然後我們利用這個點來求出對於其他點的最短距離 1. 首先進行一次鬆弛操作 將s可以直接到達的點的距離dis[i]記錄下來 然後更新i點的距離（如果比當前已知的s到i的最短距離更短的話） 2. 從U集合中選出一個距離s最短的點 將其加入到S集合中 然後利用這個點再去更新另外一些點的距離 3. 在新出現的點中選出距離s最短的點 加入到S集合中 然後再利用新點再去更新其他點距離 4. 重複以上步驟知道目標點距離源點s的距離求出或者無法再更新 * 下面是圖例演示 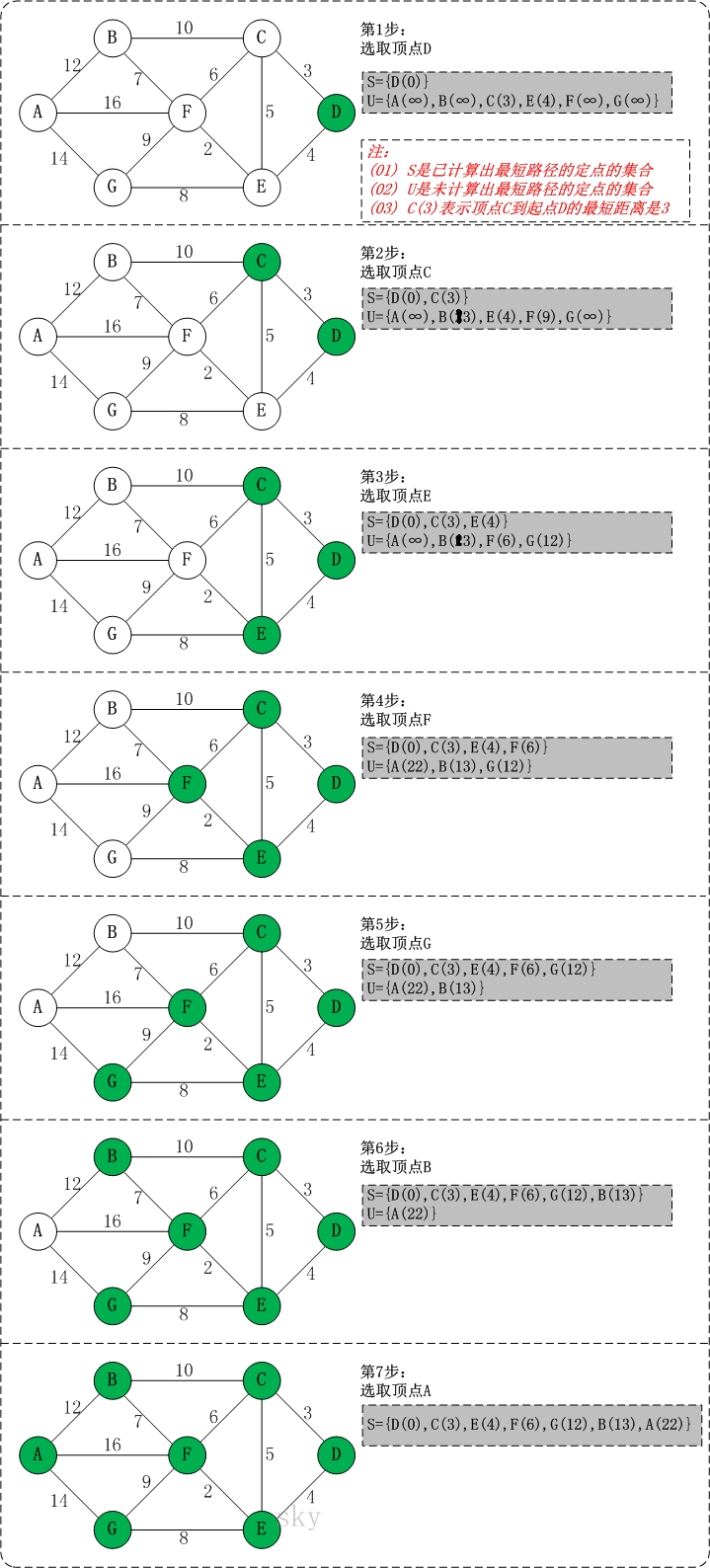 ###核心程式碼實現 ： ```cpp void dij(int s){ memset(vis,0,sizeof(vis)); vis[s] = 1;//將s放入S集合 for(int i = 1;i <= n;++i){ if(g[s][i]){dis[i] = g[s][i];}//如果從s到i有路的話 就將s到i的距離設定為長度 else dis[i] = 0x3f3f3f3f;//將其他點設定為正無窮（即目前無法到達） } dis[s] = 0;//源點s到自己的最短距離是0 for(int i = 1;i < n;++i){//遍歷每一個點以求出每一個點距離源點的最小距離 int Min = 0x3f3f3f3f,k = 0;//Min維護這一輪維護後要放入S集合的距離最小值，k維護要放入S集合的點 for(int j = 1;j <= n;++j) if(!vis[j] && Min > dis[j]){//如果點j還沒有在S集合中並且s到當前節點的距離更小 Min = dis[j];k = j; } vis[k] = 1;//k放入S集合 for(int j = 1;j <= n;++j){ if(g[k][j] && dis[j] > dis[k] + g[k][j]){//如果可以通過k鬆弛 dis[j] = dis[k] + g[k][j];//更新到j的最小值 } } } } ```
關於優化： * 上一個只是樸素的最短路演算法 有的時候並不能滿足我們的要求（~~和出題人喪心病狂的卡空間時間~~） * 我們可以用鄰接表去存邊 後面遍歷的時候就可以用鄰接表了 這樣的時間複雜度大約是常數 遠低於樸素演算法的O(n) * 求集合外的點到源點的最小值我們可以建一個小根堆，這樣我們的時間複雜度就是進堆的時間消耗 ， 為O$(Elog_E$),（E為邊數），這裡用優先佇列進行操作 ###核心程式碼實現： ```cpp void dij(int x){ priority_queue q; memset(vis,0,sizeof(vis)); memset(dis,0x3f,sizeof(dis)); dis[x] = 0; q.push(node(x,0)); while(!q.empty()){ node t = q.top();q.pop(); int k = t.num; if(vis[k])continue; vis[k] = 1; for(int i = head[k];i;i = a[i].next){ int v = a[i].to; if(dis[v] > dis[k] + a[i].dis){ dis[v] = dis[k] + a[i].dis;q.push(node(v,dis[k] + a[i].dis)); } } } } ```
##Bellman-ford演算法 * 適用範圍 : 基本啥也能用 （前提是不考慮時間複雜度情況下） * 演算法思想：和dij很像 但是這裡是沿著邊進行鬆弛操作 * 對於有向帶權圖， 從源點s開始，利用Bellman-ford，依次求解各頂點的最短距離， 演算法概況： ```cpp for(int i = 0;i < n;++i)//列舉頂點 for each(i,j)//對於每一條邊 song_chi(i,j)//鬆弛操作 ``` * BF演算法對每一條邊做鬆弛操作 ， 並且重複了n次，因此演算法的時間複雜度為O(n*E) ###核心程式碼實現： ```cpp void BF(int u){ memset(d,0x3f,sizeof(d)); d[u] = 0; for(int i = 1;i < n;++i){ for(int j = 1;j <= cnt;++j){//cnt存的是圖中共有幾個邊 int x = a[j].from,y = a[j].to,z = a[j].dis; d[y] = min(d[y],d[x] + z);//鬆弛操作 } } } ``` * ~~買一送一 BF演算法更加實惠 噹噹噹噹噹~~ 咳咳 既然dij和BF感覺實現方法差不多 但是BF有一個dij不能企及的地方：判負環 如果我們通過BF演算法求得了各個點到源點s的最短路 然後再進行一次鬆弛呢？ 如果有負環的話是不是我們會再重新跑一遍負環然後讓各個點的值更小？ 所以利用這個性質我們就可以來判斷是否有負環啦！ ```cpp bool check(){ for(int i = 1;i <= cnt;++i){ int x = a[i].from,y = a[i].to,z = a[i].dis; if(d[y] < d[x] + z)return 1; } return 0; } //主函式中： if(check()){ printf("NO\n");return 0; } ```
##SPFA演算法 * 適用範圍：反正BF能用的它都能用（文章開頭說過它可以看成是BF的優化） * BF每次都通過所有的邊來鬆弛出一個新點的最短距離 但是這樣太浪費了 * 只有那些已經鬆弛過的點才可能去鬆弛別的點，所以我們可以用一個佇列來記錄鬆弛成功了的點，以此用這些點來鬆弛鄰接點（顯然優化不小吧 能寫這個就寫這個 嘿嘿 ~~如果你剛剛看過BF並且苦思冥想請不要怪罪博主 還能提高程式碼能力的~~） ###核心程式碼實現 ```cpp struct node{ int to,dis,next; }a[maxn]; void add(int x,int y,int z){ a[++cnt].to = y;a[cnt].next = head[x];a[cnt].dis = z;head[x] = cnt; } bool spfa(int s){ memset(dis,0x3f,sizeof(dis));dis[s] = 0;//dis存到源點的最短距離 queueq; q.push(s);flag[s] = 1;//s入隊 while(!q.empty()){ int u = q.front();q.pop();flag[u] = 0;//因為一個節點u可能多次進隊 for(int i = head[u];i;i = a[i].next){//鄰接表存邊 int v = a[i].to; if(dis[v] > dis[u] + a[i].dis){//鬆弛操作：沒錯，還是我！！！ dis[v] = dis[u] + a[i].dis; if(!flag[v]){//優化 if(++num[v] >= n)return 0;如果同一個點被多次鬆弛 那麼肯定有負環（這個判斷也比剛才的少女口阿 把前輩666扣在公屏上） q.push(v);flag[v] = 1;//v進隊，標記 } } } } return 1; } //主函式中： if(!spfa(源點))輸出NO else 輸出距離 ``` 好了 本文閱讀到此結束了
碼字不易 推薦走起 ------------------------------------------------------------------------------------------------- 如果您有不懂的地方 或者 您發現程式碼有問題可以在下方評論或者給博主留言 感謝觀看>_<