**文章轉自公眾號【機器學習煉丹術】** [TOC] 本文的重點排序方法在：**氣泡排序，歸併排序，快速排序，桶排序**。 ## 演算法分類 十種常見排序演算法可以分為兩大類： **比較類排序**：通過比較來決定元素間的相對次序，由於其時間複雜度不能突破O(nlogn)，因此也稱為非線性時間比較類排序。 **非比較類排序**：不通過比較來決定元素間的相對次序，它可以突破基於比較排序的時間下界，以線性時間執行，因此也稱為線性時間非比較類排序。  **【演算法複雜度】**  **【相關概念】** * **穩定**：如果a原本在b前面，而a=b，排序之後a仍然在b的前面。 * **不穩定**：如果a原本在b的前面，而a=b，排序之後 a 可能會出現在 b 的後面。 * **時間複雜度**：對排序資料的總的操作次數。反映當n變化時，操作次數呈現什麼規律。 * **空間複雜度：**是指演算法在計算機內執行時所需儲存空間的度量，它也是資料規模n的函式。 ### 氣泡排序(重點) - Bubble Sort **【演算法描述】** * 比較相鄰的元素。如果第一個比第二個大，就交換它們兩個； * 對每一對相鄰元素作同樣的工作，從開始第一對到結尾的最後一對，這樣在最後的元素應該會是最大的數； * 針對所有的元素重複以上的步驟，除了最後一個； * 重複步驟1~3，直到排序完成。 **【動圖演示】**  ### 選擇排序 - Selection Sort - 表現最穩定的排序演算法之一，因為無論什麼資料進去都是O(n2)的時間複雜度，所以用到它的時候，資料規模越小越好。唯一的好處可能就是不佔用額外的記憶體空間了吧。理論上講，選擇排序可能也是平時排序一般人想到的最多的排序方法了吧。 **【演算法描述】** 選擇排序(Selection-sort)是一種簡單直觀的排序演算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然後，再從剩餘未排序元素中繼續尋找最小（大）元素，然後放到已排序序列的末尾。以此類推，直到所有元素均排序完畢。 **【動圖演示】**  ### 插入排序 - Insertion Sort **【演算法描述】** 一般來說，插入排序都採用in-place在陣列上實現。具體演算法描述如下： * 從第一個元素開始，該元素可以認為已經被排序； * 取出下一個元素，在已經排序的元素序列中從後向前掃描； * 如果該元素（已排序）大於新元素，將該元素移到下一位置； * 重複步驟3，直到找到已排序的元素小於或者等於新元素的位置； * 將新元素插入到該位置後； * 重複步驟2~5。 **【動圖演示】**  ### 歸併排序（重點） - Merge Sort - 歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法（Divide and Conquer）的一個非常典型的應用。將已有序的子序列合併，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。**若將兩個有序表合併成一個有序表，稱為2-路歸併。** - 是遞迴的思想 - 歸併排序是一種**穩定的排序方法**。和選擇排序一樣，歸併排序的效能不受輸入資料的影響，但表現比選擇排序好的多，因為始終都是O(nlogn）的時間複雜度。**代價是需要額外的記憶體空間。** **【演算法描述】** * 把長度為n的輸入序列分成兩個長度為n/2的子序列； * 對這兩個子序列分別採用歸併排序； * 將兩個排序好的子序列合併成一個最終的排序序列。 **【動圖演示】**  ### 快速排序（重點） - Quite Sort - 快速排序的基本思想：通過一趟排序將待排記錄分隔成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分的關鍵字小，則可分別對這兩部分記錄繼續進行排序，以達到整個序列有序。 - 之前一直以為快排和二分法有關，但是其實是分治法的應用。 **【演算法描述】** 快速排序使用分治法來把一個串（list）分為兩個子串（sub-lists）。具體演算法描述如下： * 從數列中挑出一個元素，稱為 “基準”（pivot）； * 重新排序數列，所有元素比基準值小的擺放在基準前面，所有元素比基準值大的擺在基準的後面（相同的數可以到任一邊）。在這個分割槽退出之後，該基準就處於數列的中間位置。這個稱為分割槽（partition）操作； * 遞迴地（recursive）把小於基準值元素的子數列和大於基準值元素的子數列排序。 **【動圖演示】**  ### 堆排序（重點） - **python中sort排序的方法就是堆排序** - 堆排序（Heapsort）是指利用堆這種資料結構所設計的一種排序演算法。堆積是一個近似完全二叉樹的結構，並同時滿足堆積的性質：即子結點的鍵值或索引總是小於（或者大於）它的父節點。 **【演算法描述】** 這個比較複雜。先看動圖然後慢慢細說。 **【動圖演示】**  **【分步詳解】** - 堆（二叉堆）可以視為一棵完全的二叉樹。完全二叉樹的一個優秀的性質就是，**除了最底層之外，每一層都是滿的** - 二叉堆一般分為兩種：**最大堆和最小堆。** - **最大堆** ：最大堆中的最大元素在根結點（堆頂）；堆中每個父節點的元素值都大於等於其子結點（如果子節點存在） - **最小堆**：最小堆中的最小元素出現在根結點（堆頂）；堆中每個父節點的元素值都小於等於其子結點（如果子節點存在） 假設我們要對目標陣列A {57, 40, 38, 11, 13, 34, 48, 75, 6, 19, 9, 7}進行堆排序。 首先第一步和第二步，建立堆，這裡我們用最大堆；建立過程中，保證調整堆的特性。從最後一個分支的節點開始進行調整為最大堆。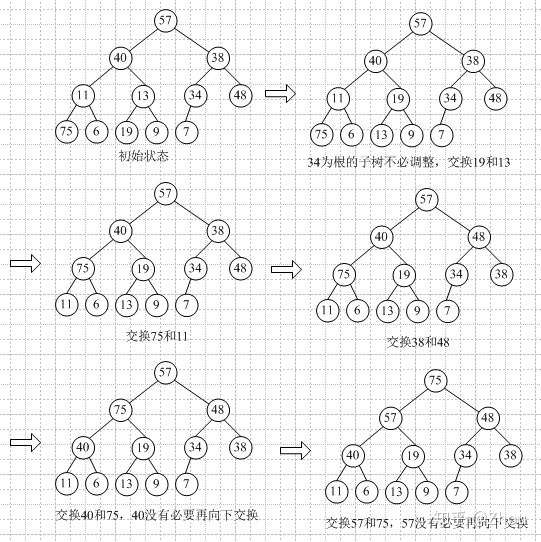  現在得到的最大堆的儲存結構如下：  接著，最後一步，堆排序，進行（n-1）次迴圈。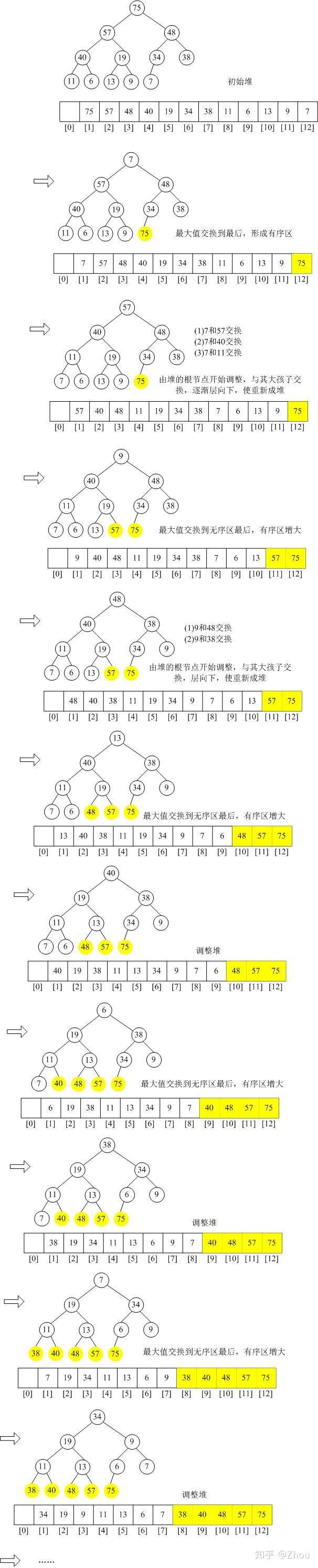  這個迭代持續直至最後一個元素即完成堆排序步驟。 **【個人理解】** 通過堆這個結構，讓隨機兩個陣列進行比大小，然後讓獲勝者之間再比大小，這樣就可以通過複雜都logn得到一個最大的數字。然後不考慮這個數字，在剩下的數字中重複這個過程。**有點類似比賽半決賽，四分之一決賽，八強這樣的感覺。** ### 計數排序 - Counting Sort - 計數排序不是基於比較的排序演算法，其核心在於將輸入的資料值轉化為鍵儲存在額外開闢的陣列空間中。 作為一種線性時間複雜度的排序，計數排序要求輸入的資料必須是有確定範圍的整數。**敲黑板!計數排序不是基於比較的，所以是線性時間複雜度，但是速度快的代價就是對輸入資料有限制要求：確定範圍的整數** **【演算法描述】** **這部分不怎麼用看，直接看動圖就理解了** * 找出待排序的陣列中最大和最小的元素； * 統計陣列中每個值為i的元素出現的次數，存入陣列C的第i項； * 對所有的計數累加（從C中的第一個元素開始，每一項和前一項相加）； * 反向填充目標陣列：將每個元素i放在新陣列的第C(i)項，每放一個元素就將C(i)減去1。 **【動圖演示】**  ### 基數排序 - Radix Sort - 基數排序是按照低位先排序，然後收集；再按照高位排序，然後再收集；依次類推，直到最高位。**有時候有些屬性是有優先順序順序的，先按低優先順序排序，再按高優先順序排序。**最後的次序就是高優先順序高的在前，高優先順序相同的低優先順序高的在前。 **【演算法描述】** * 取得陣列中的最大數，並取得位數； * arr為原始陣列，從最低位開始取每個位組成radix陣列； * 對radix進行計數排序（利用計數排序適用於小範圍數的特點）； **【動圖演示】**