整合演算法往往被稱為三個臭皮匠，賽過一個諸葛亮，整合演算法的起源是來自與PAC中的強可學習和弱可學習，如果類別決策邊界可以被一個多項式表示，並且分類正確率高，那麼就是強學習的，如果分類正確率不高，僅僅只是比隨機猜測好一點，那麼就是弱可學習，後來有人證明強可學習和弱可學習是等價的，那麼弱可學習就可以提升為強可學習，整合就是其中一個方法。本文的程式碼都在我的[github](https://github.com/yzzyq/machingLearning)。 [toc] ##引言 不過三個臭皮匠真的能賽過一個諸葛亮嗎？很明顯不是，一個科研專家並不是幾個普通人就能比得上的，很多時候，一個人能比得上千軍萬馬，而且這裡的皮匠是裨將的意思，也就是副將，他們可以從不同的角度來指出問題的所在，這才能抵得上只在大營中的諸葛亮。那麼多個學習器的組合，真的能獲得比最好的單一學習器更好的效能嗎？生活中總說不怕神一樣的隊友，只怕豬一樣的隊友，這裡的單一學習器最好是好而不同，這就是整合演算法的倆個核心，就是準確性和多樣性，那麼滿足了好而不同就能更好嗎？在實驗中，訓練資料往往並不能包含全部的資料情況，在資料不充分的條件下，如果我們從不同的假設空間角度來學習或者學習到不同資料分佈的假設，並且學習的都是正確的，那麼就能從多角度來看待問題，這樣就能減小錯誤的風險了。所以並不是隨便幾個演算法整合起來就能夠得到一個更好的結果，這幾個演算法必須要多樣並且準確。 但是準確性和多樣性是存在衝突，準確率很高之後，再提升多樣性就會犧牲準確率，因為準確率高了之後，說明模型與訓練資料分佈的偏差很低了，這時的模型往往就會固定成一個樣子，因而就沒有多樣性，泛化能力就降低了，方差就會變大，這也是整合演算法的核心問題，偏差小了，方差自然就大，大白話就是在訓練資料上的準確率很高的話，在測試資料上的準確率就不行了，沒有很強的泛化能力，產生過擬合現象。那麼從降低方差和降低偏差的倆個角度來看，自然就有了倆種思路bagging和boosting。補充一下偏差和方差，偏差指的是演算法的期望預測與真實預測之間的偏差程度，反應了模型本身的擬合能力；方差度量了同等大小的訓練集的變動導致學習效能的變化，刻畫了資料擾動所導致的影響。 ##bagging 如果模型偏差小，方差很大，比如不剪枝的決策樹就容易過擬合，那麼如何降低方差，自然要從多樣性入手，多樣性有倆種分別是資料多樣性和模型多樣性。對於資料多樣性，在面對同一堆資料，可以採用有放回的取樣，就是隨便選擇一個數據，再把資料放回到資料集，之後再選擇。這樣重複並且重疊的取樣方式產生了樣本擾動，具有了多樣性。對於模型多樣性，採用的都是效能較好的相互獨立的分類器，這裡的相互獨立非常重要，這就讓模型之間沒有了依賴關係，每個人都可以從自己的角度來思考問題。那麼我們就可以使用有放回的取樣得到多個數據集，用這些資料集分別訓練多個獨立模型，再將這些模型的結果結合，這就是Bagging的基本思想了。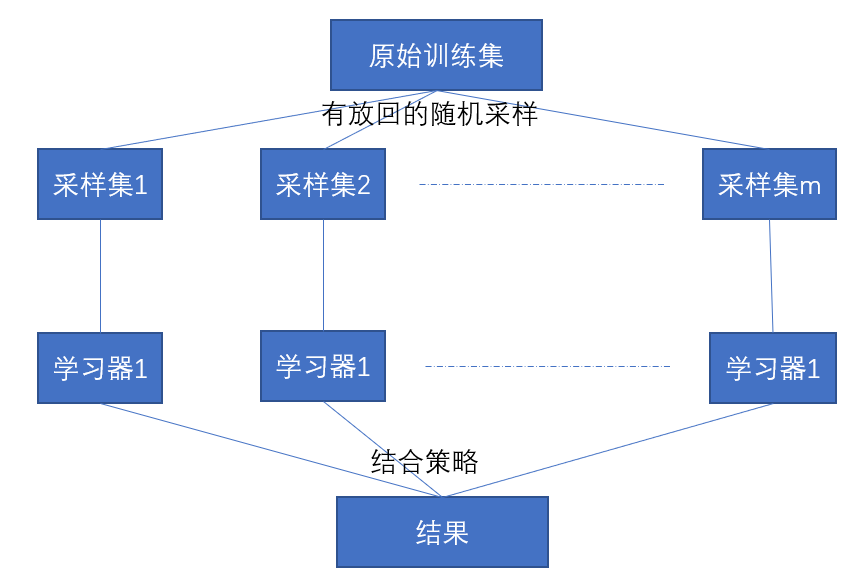過程可以看下圖 之前講過決策樹演算法，決策樹演算法就是易受資料的擾動，這個其實就是決策樹過擬合的表現。之前也說過這種過擬合的表現其實也被稱為偏差小，方差大。如果對決策樹進行bagging的話，就會形成random forest。 ###隨機森林(random forest) 隨機森林就是以決策樹為基學習器構建bagging整合的基礎上，進一步在決策樹訓練過程中引入隨機屬性選擇。就是每個基分類器都是決策樹，但是基決策樹的特徵選擇都是從該特徵集合中隨機一個子集，從子集中選出最優的，這種屬性擾動生成的每個決策樹都是獨立並且不同，就能做到模型多樣性。之後使用有放回的取樣資料，形成每個決策樹的訓練資料，這樣就能做到了樣本擾動。這樣不同資料，隨機屬性生成的多個決策樹就能滿足整合演算法的要求。 在之前我實現的隨機森林中，對於特徵的隨機選擇，有倆種思路，一種就是每一個結點都是隨機選擇一些特徵，選擇其中最好的特徵，通常是log2d，還有一種就是也可以每棵樹只選擇固定的特徵子集來選擇。對於實現，我的程式碼中使用的就是第二種，對每棵樹選出特徵子集來對樹進行建立。 ``` // 提取資料 dataSet,labelSet = dataSE.extractData() #森林中數的個數 numTree = 50 #森林 forest = [] #檢視每個資料的選中情況 choiceDataNum = [0 for i in range(len(dataSet))] #建立每棵決策樹 for i in range(numTree): #首先選出資料集和特徵子集 childData,chidFeatures,noUseData = randomSample(dataSet,labelSet) #建立決策樹 childTree = Tree.buildTree(childData,chidFeatures) Tree.printTree(childTree) forest.append(childTree) for i in range(len(noUseData)): choiceDataNum[i] += noUseData[i] testData = produceData(choiceDataNum,dataSet) results = [] correct = 0 #開始測試每個測試集 for data in testData: results = [] for tree in forest: result = Tree.classify(data,tree,labelSet) #print(list(result.keys())) results.append(list(result.keys())) #print(results) feaNum = 0 noFeaNum = 0 resultData = 'feafits' #採用投票法，票數最多的就是類別 for i in range(len(results)): #print('result[i]',results[i]) if results[i][0] == 'feafits': feaNum += 1 else: noFeaNum += 1 #print(feaNum,noFeaNum) if feaNum < noFeaNum: resultData = 'nofeafits' print('結果是',resultData) results.append(resultData) print('實際結果是：',data[-1]) if resultData == data[-1]: correct += 1 ccur = (correct / len(testData))*100 print('精確度:',ccur) ``` ##boosting boosting方法是關注偏差，基於效能相當弱的簡單學習器構建出很強的整合。它不像bagging，各學習器都是獨立的，它的學習器之間具有很強的依賴關係，這是因為它關注的是降低偏差，所以它做的就是每次都會在上一輪基礎上更加擬合原資料，這樣就可保證偏差，既然訓練過程出來的模型能夠保證偏差，那麼需要選擇方差更小的單個學習器，就是更簡單的學習器。我們也可以看成它是通過不斷地調整樣本分佈來訓練學習器，使得學習器針對不同的訓練資料分佈，它更像每個人就只學習一種技能，最後大家合在一起使用幹活，少了誰都不行。 有一些演算法是通過調整資料權重來調整樣本分佈的，而資料權重是通過loss調整。但是在這個思想基礎下，有著倆個不同的想法，第一個就是如果樣本訓練的不夠好，也就是模型無法擬合這個資料，那麼對於這個樣本要給予更高的權重，這類工作就是hard negative mining和focal loss，第二個想法就是從易到難學習，慢慢增加難度，最終如果還有樣本的loss依舊很大，那麼認為這類樣本是離群點，強行擬合很容易造成效能的下降，這類工作就是curriculum learning和self-paced learning。可以看出這倆種演算法思想基本上是完全相反，第一類認為模型擬合不好的資料，應該盡力去fit，第二種認為模型擬合不好的資料，可能是訓練的標籤有誤，這其實是對資料分佈的不同假設的緣故，如果感興趣可以看看這篇[文章](https://zhuanlan.zhihu.com/p/53545036)，而我們的adaboost就是第一種。 ###adaboost adaboost通過調整資料權重來不斷地調整樣本分佈，並且使用的是增大分類錯誤的樣本權重，使後面的學習器更加關注那些分類錯誤的資料，按照這樣的過程重複訓練出M個學習器，最後進行加權組合，它更像我們高中時期記錯題到錯題集中，然後在錯題集上反覆做的過程。具體演算法過程如下圖所示

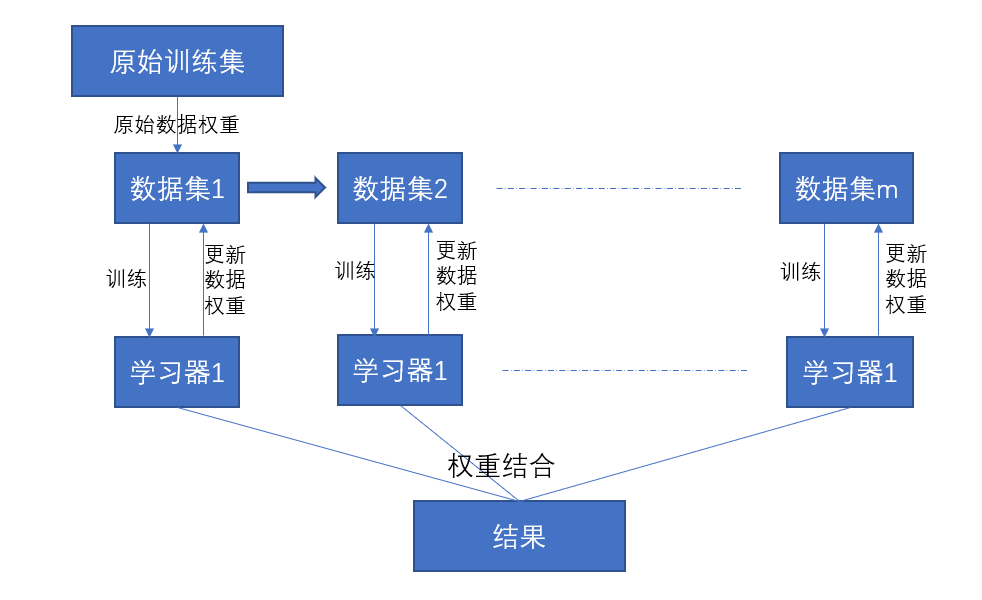
從上面看出我們需要更新資料權重，還需要得到各學習器的權重進行結合。這裡就有了倆個問題，如何更新資料權重？如何確定各學習器的權重？那麼我們就推導一下這個演算法是如何出來的，首先假設的就是模型為加法模型，損失函式是指數損失。 先來看我們的模型函式就是$f(x) = \sum\limits_{m=1}^M\alpha_mG_m(x)$，指數損失函式就是$L(y,f(x)) = e^{-yf(x)}$，假設模型在m次迭代中，前m-1個係數$\alpha$和基學習器$G(x)$都是固定的，那麼模型函式就會變成$f_m(x) = f_{m-1}(x) + \alpha_mG_m(x)$，這樣的話，最小化損失函式與$\alpha_m$和$G_m(x)$有關。那麼現在我們的目標就是損失函式最小的時候，求出$\alpha_m$和$G_m(x)$的值，公式表示如下 $$(\alpha_m, G_m(x)) = argmin\sum\limits_{i = 1}^Ne^{-y_if_m(x_i)}$$ 這裡的N就是N個訓練資料$((x_1,y_1),(x_2, y_2),...(x_N, y_N))$。 $$(\alpha_m, G_m(x)) = argmin\sum\limits_{i = 1}^Ne^{-y_i(f_{m-1}(x_i) + \alpha_mG_m(x_i))}$$ $$(\alpha_m, G_m(x)) = argmin\sum\limits_{i = 1}^Ne^{-y_i(f_{m-1}(x_i))} e^{-y_i\alpha_mG_m(x_i)}$$ 我們設定$w_i^m = e^{-y_i(f_{m-1}(x_i))}$，代入其中 $$(\alpha_m, G_m(x)) = argmin\sum\limits_{i = 1}^Nw_i^me^{-y_i\alpha_mG_m(x_i)}$$ 之後我們將整個資料集分成倆部分，一部分是分類正確的，還有一部分是分類錯誤的 $$(\alpha_m, G_m(x)) = argmin(e^{-\alpha_m}\sum\limits_{y = G_m(x)}w_i^m + e^{\alpha_m}\sum\limits_{y \neq G_m(x)}w_i^m)$$ 下面將之轉化成只有$y \neq G_m(x)$的資料 $$(\alpha_m, G_m(x)) = argmin(e^{-\alpha_m}(\sum\limits_{n=1}^Nw_i^m - \sum\limits_{y \ne G_m(x)}w_i^m) + e^{\alpha_m}\sum\limits_{y \neq G_m(x)}w_i^m)$$ $$(\alpha_m, G_m(x)) = argmin(e^{-\alpha_m}\sum\limits_{n=1}^Nw_i^m + (e^{\alpha_m} - e^{-\alpha_m})\sum\limits_{y \ne G_m(x)}w_i^m)$$ 這裡最終的式子可以看出最小化損失函式就是最小化帶權誤差率，誤差率就是$\epsilon_m = \frac{\sum\limits_{y \ne G_m(x)}w_i^m}{\sum\limits_{n=1}^Nw_i^m}$，我們對最終的式子求$\alpha_m$導數使之等於0就能得到 $$-e^{-\alpha_m}\sum\limits_{n=1}^Nw_i^m + (e^{\alpha_m} + e^{-\alpha_m})\sum\limits_{y \ne G_m(x)}w_i^m = 0$$ $$e^{\alpha_m}\sum\limits_{y \ne G_m(x)}w_i^m - e^{-\alpha_m}\sum\limits_{y = G_m(x)}w_i^m = 0$$ 式子的倆邊同時乘以$e^{\alpha_m}$可以得到 $$e^{2\alpha_m}\sum\limits_{y \ne G_m(x)}w_i^m - \sum\limits_{y = G_m(x)}w_i^m = 0$$ $$e^{2\alpha_m}\sum\limits_{y \ne G_m(x)}w_i^m = \sum\limits_{y = G_m(x)}w_i^m$$ $$e^{2\alpha_m} = \frac{\sum\limits_{y = G_m(x)}w_i^m}{\sum\limits_{y \ne G_m(x)}w_i^m}$$ 我們可以根據誤差率式子$\epsilon_m = \frac{\sum\limits_{y \ne G_m(x)}w_i^m}{\sum\limits_{n=1}^Nw_i^m}$，將上面的式子進行化簡 $$e^{2\alpha_m} = \frac{1 - \epsilon_m}{\epsilon_m}$$ $$\alpha_m = \frac{1}{2}ln\frac{1 - \epsilon_m}{\epsilon_m}$$ 這裡我們就得到了分類器的權重$\alpha_m = \frac{1}{2}ln\frac{1 - \epsilon_m}{\epsilon_m}$，我們再回頭看我們的模型函式$f_m(x) = f_{m-1}(x) + \alpha_mG_m(x)$，從$w_i^m = e^{-y_i(f_{m-1}(x_i))}$，我們可以轉化成$w_i^{m+1} = e^{-y_i(f_m(x_i))}$，帶入其中就是 $$w_i^{m+1} = e^{-y_i(f_{m-1}(x_i) + \alpha_mG_m(x_i))}$$ $$w_i^{m+1} = e^{-y_if_{m-1}(x_i)} e^{-y_i\alpha_mG_m(x_i)}$$ 我們知道$w_i^m = e^{-y_i(f_{m-1}(x_i))}$，帶入其中就是 $$w_i^{m+1} = w_i^me^{-y_i\alpha_mG_m(x_i)}$$ 最終再加入一個規範化因子$Z_m$，使得$w^{m+1}$成為一個概率分佈 $$w_i^{m+1} = \frac{w_i^m}{Z_m}e^{-y_i\alpha_mG_m(x_i)}$$ 其中規範化因子就是 $$Z_m = \sum\limits_{i=1}^Nw_i^me^{-\alpha_my_iG_m(x_i)}$$ 這樣就得到了權重的更新公式就是$w_i^{m+1} = \frac{w_i^m}{Z_m}e^{-y_i\alpha_mG_m(x_i)}$，我們還可以從權重公式$w_i^{m+1} = w_i^me^{-y_i\alpha_mG_m(x_i)}$可以看出，如果分類正確，那麼$y_i = G_m(x_i)$，那麼權重的更新就是$w_i^{m+1} = w_i^me^{-\alpha_m}$，權重就是在減少，反之就是在增大。 此時我們可以得出adaboost演算法的全部過程： 1. 設定每個樣本的初始權重值 2. 將資料、類別和樣本權重放入弱學習器中，選出分類效果最好的 （1）根據列來迴圈，計算出步長，用於後面選擇閾值 （2）迴圈閾值來進行切分，找出最好的那個，並且記錄列，閾值，正反 （3）找出所有列中最好的那個閾值返回 補充:這裡是只是根據一個維度進行切分，因而每次都是在所有列中選擇 4. 根據錯誤率計算alphas，更新權重值，並且計算alpha值 5. 將此分類放入弱學習器結果中 6. 利用alpha和結果計算值，利用sign來檢視錯誤，錯誤為0，則完成，否則繼續 下面我們再看一個例子來加深一下印象， | 序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | | x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 我們的基礎學習器使用的是樹樁決策樹。首先初始化每個樣本的權重，我們使用的是平均值，那麼$w_i^{1} = 0.1$， 對m=1，之後根據權重和資料設定基學習器，因為是樹樁，我們只要找出閾值使得誤差率最低就好了，先找出所有的切分點1.5，2.5，3.5，4.5，5.5，6.5，7.5，8.5，9.5，之後計算所有切分點的誤差率，找出最低誤差率的時候切分點為2.5，誤差率就是$\epsilon_1 = \frac{0.3}{1} = 0.3$， $$ G_1(x) = \begin{cases} 1 & x < 2.5,\\ -1 & x>2.5 \end{cases} $$ 然後根據上面的公式$\alpha_m = \frac{1}{2}ln\frac{1 - \epsilon_m}{\epsilon_m}$來求我們得出的這個基分類器的權重， $$ \alpha_1 = \frac{1}{2}ln\frac{1 - \epsilon_1}{\epsilon_1} = \frac{1}{2}ln\frac{1 - 0.3}{0.3} = 0.4236 $$ 之後根據上面得到的權重更新公式$w_i^{m+1} = \frac{w_i^m}{Z_m}e^{-y_i\alpha_mG_m(x_i)}$，先計算規範化因子$Z_m$，它的公式就是$Z_m = \sum\limits_{i=1}^Nw_i^me^{-\alpha_my_iG_m(x_i)}$ $$ Z_1 = \sum\limits_{i=1}^Nw_i^1e^{-\alpha_1y_iG_1(x_i)} = w_1^1e^{-\alpha_1y_1G_1(x_1)} + w_2^1e^{-\alpha_1y_2G_1(x_2)} + \dots \ + w_{10}^1e^{-\alpha_1y_{10}G_1(x_{10})} \\ = 0.1\times e^{-0.4236} + 0.1e^{-0.4236} + \dots \\ = 0.1e^{-0.4236}\times7 + 0.1e^{0.4236} \times3 = 0.9165 $$ 之後計算$w_1^2$ $$ w_1^{2} = \frac{w_1^1}{Z_1}e^{-y_1a_1G_1(x_1)} = 0.07143 $$ 然後依次更新所有資料權重，最後得到(0.07143，0.07143，0.07143，0.07143，0.07143，0.07143，0.16667，0.16667，0.16667，0.07143)，此時的分類器就是$f_1(x) = 0.4236G_1(x)$，將這個$sign(f_1(x))$來測試所有的訓練集，發現錯了三個，那麼繼續更新。 對於 m = 2，先計算所有切分點的誤差率，可以得到8.5的時候誤差率最低，最低$\epsilon_2 = \frac{0.07143\times3}{0.07143\times7+0.16667\times3} = 0.2143$，和上面的過程一樣計算基分類器的權重$\alpha_2 = 0.6496$，再更新所有資料的權重，此資料上有三個誤分類點，此時的分類器就是$f_2(x) = 0.4236G_1(x) + 0.6496G_2(x)$，將這個$sign(f_2(x))$來測試所有的訓練集，發現錯了三個，那麼繼續更新。 對於 m = 3，先計算所有切分點的誤差率，可以得到5.5的時候誤差率最低，最低$\epsilon_3 = 0.1820$，和上面的過程一樣計算基分類器的權重$\alpha_3 = 0.7514$，再更新所有資料的權重，此資料上有三個誤分類點，此時的分類器就是$f_3(x) = 0.4236G_1(x) + 0.6496G_2(x) + 0.7514G_3(x)$，將這個$sign(f_3(x))$來測試所有的訓練集，發現全部正確，那麼停止完成。 那麼最終的分類器就是 $$ G(x) = sign[f_3(x)] = sign[0.4236G_1(x) + 0.6496G_2(x) + 0.7514G_3(x)] $$ ``` #numIt就是迴圈次數，返回整個分類器 def adaboostTraining(dataSet,labelSet,numIt = 40): dataMat = np.mat(dataSet) ResultMat = np.mat(labelSet).T weakResult = [] m,n = dataMat.shape #判斷資料是否已經分類好了 result = np.mat(np.zeros((m,1))) #設定出初始樣本權重值 Weights = np.mat(np.ones((m,1))/m) for i in range(numIt): #選擇最好的弱學習器 stumpClass,errorRate,classResult = choiceBestWeak(dataMat,\ ResultMat,Weights) #計算出alphas的值,防止錯誤率為0時 alphas = float(0.5*np.log((1-errorRate)/max(errorRate,1e-16))) stumpClass['alphas'] = alphas #放入到結果學習器中 weakResult.append(stumpClass) #更新樣本權重值 temp = np.multiply(-1*alphas*ResultMat,classResult) #print('temp',temp) tempTop = np.multiply(Weights,np.exp(temp)) Weights = tempTop/sum(Weights) #檢視是否分類完全正確,全部分類正確就完成 #print('alphas',alphas) #print('classResult',classResult) result += alphas*classResult error = np.multiply(np.sign(result) != ResultMat\ ,np.ones((m,1))) errorR = error.sum()/m #print('errorR',errorR) if errorR == 0: break return weakResult ``` 那麼adaboost為什麼要用指數損失函式，可不可以使用其他的損失函式？當然也是可以的，但是如果用了其他的損失函式，推導過程就不同，並且只是boosting家族中的另一個演算法而已了，adaboost使用指數損失函式就是計算和表達簡單，我們可以從下表看一下換損失函式會變成什麼演算法。

如果使用adaboost對一些好分割的資料進行分類的話，你會發現，adaboost不會過擬合，並且還會出現一個特別奇怪的現象：當訓練集的誤差率減小到0的時候，如果你繼續增加基礎分類器，也就是讓演算法繼續執行下來，它的測試誤差率也會下降。這一點周志華老師在2014年的CCL中也討論過，其中能解釋比較清楚的就是Boosting Margin，一組資料它的測試誤差率能夠達到0，說明資料集比較好分割，margin也就可以看成是它分類的置信度，也許剛開始分類的時候，它只有60%的把握分對，之後再繼續訓練，就有了80%的把握，margin就可以看成這個置信度，confidence變得越來越大，決策邊界自然也會越來越公正，自然結果也更加可靠了，後面SVM還會談到這個margin。 ###提升樹 提升樹是以分類樹或者回歸樹作為基本分類器的提升方法，並且有著大量的引用，一度被認為是與SVM一樣具有很強泛化能力的演算法。與adaboost使用資料權重不同，普通的提升樹是利用殘差進行計算的，並且多用於迴歸問題中，利用最小均方損失函式學習殘差迴歸樹。對於它的過程，我們可以先來大概看一下cart迴歸樹的過程，利用最小化均方誤差來找出最優屬性的最好切分點，首先就是找出一個屬性的所有切分點，然後對所有的切分點做均方誤差，找出最小誤差的那個切分點，計算所有屬性的最小切分點，得到最優屬性的最好切分點。然後將資料分成倆個分支之後，繼續在資料集上尋找最優屬性的最好切分點。普通的提升樹中的一棵迴歸樹的建立和它一樣，都是不斷地利用最小化均方誤差來找出最優屬性的最好切分點，只不過提升樹是許多回歸樹，每顆迴歸樹擬合的資料不同，從一開始的訓練資料到之後的殘差資料，最後的結果就是所有樹的結果加在一起。迴歸結果與真實結果差距越大的資料，那麼下一次殘差也越大，這其實也變相的增大了分錯的資料權重。提升樹說起來很抽象，先來整理一下過程。 1. 初始化$f_0(x) = 0$，最開始的擬合函式就是0; 2. i = 0,1,2...., 進行迴圈計算殘差，$r_{mi} = y_i - f_{m-1}(x_i)$; 3. 通過均方誤差擬合數據$((x_1,r_{m1}),(x_2,r_{m2}),....,(x_i,r_{mi}))$，學習到一個迴歸樹，得到T(x) (1). 找出一個屬性的所有切分點； (2). 計算所有切分點的均方誤差； (3). 得到均方誤差最小的那個切分點； (4). 計算出所有屬性的最好切分點，之後找出最優屬性的最好切分點，作為節點； (5). 直到每個葉子節點年齡都唯一或者葉子節點個數達到了預設終止條件，如果不唯一，葉子節點的值就是平均值，注意，它並不會刪除用過的屬性，會迴圈用； 4. 更新$f_m(x) = f_{m-1}(x) + T(x)$; 5. 達到迴圈停止條件，便得到了迴歸問題提升樹$f_M(x)$; 6. 測試的結果就是所有迴歸樹的結果相加。 普通提升樹的損失函式是均方誤差，殘差作為每一輪的損失，而且均方誤差能夠很好的擬合殘差，但是損失函式有很多種，這些一般性的損失函式無法很好的擬合殘差。對此，Freidman提出用損失函式的負梯度代替殘差作為每一輪損失的近似值，之後通過擬合負梯度每輪產生一個cart迴歸樹。 1. 初始化$f_0(x) = arg\min\limits_c\sum\limits_{i=1}^NL(y_i,c)$，這個是選取初始值，不同損失函式初始值選取不同，因為它要讓損失函式達到最小，經常對損失函式求導等於0來找出c的求解公式，因為是argmin，所以$f_0(x) = c$，比如均方差就是平均數; 2. i = 0,1,2...., 進行迴圈計算梯度，$r_{mi} = -\frac{\partial L(yi, f_{m-1}(x_i))}{\partial x_i}$; 3. 通過一般誤差函式擬合數據$((x_1,r_{m1}),(x_2,r_{m2}),....,(x_i,r_{mi}))$，學習到一個迴歸樹，得到T(x) (1). 找出一個屬性的所有切分點； (2). 計算所有切分點的一般誤差函式； (3). 得到一般誤差函式最小的那個切分點； (4). 計算出所有屬性的最好切分點，之後找出最優屬性的最好切分點，作為節點； (5). 直到每個葉子節點年齡都唯一或者葉子節點個數達到了預設終止條件，如果不唯一，葉子節點的值就是第一步中損失函式求導等於0來得到的值，注意，它並不會刪除用過的屬性，會迴圈用； 4. 更新$f_m(x) = f_{m-1}(x) + l_rT(x)$，可以設定一個學習率$l_r$; 5. 達到迴圈停止條件，便得到了迴歸問題提升樹$f_M(x)$; 6. 測試的結果就是所有迴歸樹的結果相加。 再來看一個例子熟悉一下 | 編號 | 年齡(歲) | 體重(kg) | 身高(m)標籤值 | | :---: | :---: | :---: | :---: | | 0 | 5 | 20 | 1.1 | | 1 | 7 | 30 | 1.3 | | 2 | 21 | 70 | 1.7 | | 3 | 30 | 60 | 1.8 | | 4(預測) | 25 | 65 | ? | 如果我們設定生成5棵樹，並且每棵樹的最大深度為3，學習率$l_r = 0.1$，我們使用均方差作為損失函式，這樣也能與普通提升樹聯絡起來，那麼下面來看過程 第一步就是初始化$f_0(x) = arg\min\limits_c\sum\limits_{i=1}^NL(y_i,c)$，直接對均方差損失函式進行求導，並且等於0。 $$\sum\limits_{i = 1}^{N}\frac{\partial L(y_i, c)}{\partial c} = \sum\limits_{i = 1}^{N}\frac{\partial (\frac{1}{2}(y_i - c)^2)}{\partial c} = \sum\limits_{i = 1}^{N} c-y_i$$ 令導數等於0 $$\sum\limits_{i = 1}^{N} c-y_i = 0$$ $$\sum\limits_{i = 1}^{N} c = \sum\limits_{i = 1}^{N} y_i$$ $$ c = \frac{\sum\limits_{i = 1}^{N} y_i}{N}$$ 所以初始化$c = \frac{1.1+1.3+1.7+1.8}{4} = 1.475 = f_0(x)$ 第二步就是迴圈計算梯度，先計算本次的梯度就是$-\frac{\partial L(y_i, c)}{\partial c} = y_i - c$，將之代入可以得到本次需要擬合的資料。 | 編號 | 年齡(歲) | 體重(kg) | 身高(m)標籤值 | | :---: | :---: | :---: | :---: | | 0 | 5 | 20 | -0.375 | | 1 | 7 | 30 | -0.175 | | 2 | 21 | 70 | 0.225 | | 3 | 30 | 60 | 0.325 | 第三步就是通過一般誤差函式擬合上面得到的資料，尋找回歸樹的最佳屬性的最好切分點。先看年齡，分別查找出全部的切分點，分別是6，14，25.5，然後使用誤差函式計算誤差，切分點6的時候，左邊只有資料1，右邊有資料7，21，30，先計算出左邊的MSE，只有一個數據，那肯定就是0，再計算右邊的MSE，先計算期望，$\frac{-0.175+0.225+0.325}{3} = 0.125$，然後再將資料與期望相減平方得到MSE，$(-0.175-0.125)^2 + (0.225-0.125)^2 + (0.325-0.125)^2 = 0.14$，再將倆邊的MSE相加就得到了切分點6的$MSE_6 = 0.14$，按照這個步驟計算出全部屬性的全部切分點的MSE。 | 年齡切分點6 | 年齡切分點14 | 年齡切分點25.5 | 體重切分點25 | 體重切分點45 | 體重切分點65 | | :----: | :----: | :----: | :---: | :---: | :---: | | 0.14 | 0.025 | 0.187 | 0.14 | 0.025 | 0.260 | 選擇年齡切分點14作為節點，那麼我們的樹就是

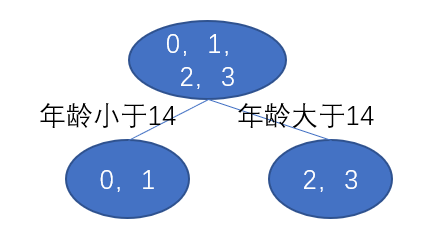
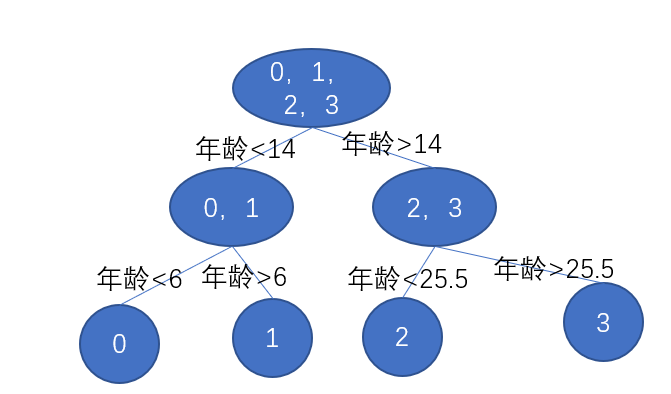
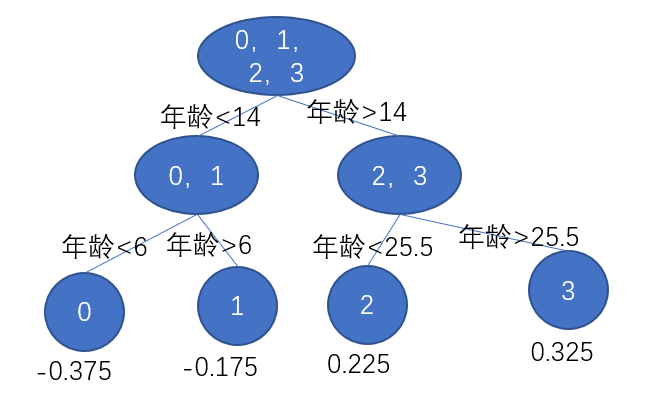
因為我設定樹的深度是3，這裡才是2，那麼還需要再來一次，先劃分左節點，左節點的資料只有0，1，按照上面的步驟計算年齡切分點6和體重切分點25的MSE， | 年齡切分點6 | 體重切分點25 | | :----: | :----: | | 0 | 0 | 我們選擇年齡切分點6，之後同樣計算右節點，同樣是選擇年齡切分點25.5，那麼最後的樹就是 我們還需要計算出葉子節點的值，我們需要對損失函式求導，等於0，第一步的時候我們就計算出來 $$ c = \frac{\sum\limits_{i = 1}^{N} y_i}{N}$$ 那麼葉子節點的值就是平均值，我們可以計算出來，那麼樹就是 第四步更新$f_1(x) = f_{0}(x) + l_rT(x)$，可以設定一個學習率$l_r$，$T(x)$就是這棵樹，如果用表示式的話，就是$f_1(x) = f_{0}(x) + l_r\sum\limits_{j=1}^{4}\Upsilon_{j1}$ 第五步就是不斷地迴圈，然後直到建立了五棵樹達到了停止條件，得到最後的迴歸樹，用數學表達就是 $$f(x) = f_{0}(x) + l_r\sum\limits_{m=1}^{5}\sum\limits_{j=1}^{4}\Upsilon_{jm}$$ 第六步就是測試資料，將測試資料放進所有的樹中，然後相加起來 $$f(x) = 1.475 + 0.1\times(0.225+0.2025+0.1823+0.164+0.1476)=1.56714$$ 如果你在競賽中使用過它，你就會發現它即使樹的深度很淺，但是依舊能夠達到很高的精度，但是隔壁的隨機森林樹的深度卻很高，你也許會認為它比隨機森林還好，其實這就是倆者的演算法特性造成，隨機森林降低的就是方差，偏差有基學習器作為保障的，boosting降低的就是偏差，方差是基學習器作為保障的，既然基學習器保障方差，那麼基學習器一定不會很深，不然就會過擬合了，方差就會減小的。 其實我們思考思考就會發現殘差不就是全域性最優方向嘛，而且殘差就是均方差損失函式的梯度，那也說明它其實也是一種特殊的梯度。 如果懂了GBDT，那麼你再看XGBoost，就能看得懂思想原理了，因為XGBoost本質上就是GBDT的一種高效的工業界實現，外加一些演算法上的優化，最主要的就是GBDT是利用的梯度，XGBoost是利用的二階泰勒展開，更加準確，並且XGBoost還利用了並行化實現和缺失值的處理等等操作。 ##總結 以前我一直覺得整合演算法可以稱得上思想和效果都很好的演算法，並且從降低方差和偏差角度出發，也能理解它的基本原理，但是你在研究中使用整合演算法的時候，要想整合演算法效果好的話，就必須要考慮基學習器的選擇，當然在競賽中，很多時候直接使用XGBoost也能得到一個很好的結果。當然整合演算法還有思考點，就是如何將所有基學習器的結果結合，這方面也有很多的方法。本文的程式碼都在我的[github](https://github.com/yzzyq/machingLearning)。