學演算法還能指導找物件?是的,這就是大名鼎鼎的穩定婚姻演算法
今天是演算法資料結構專題的第30篇文章,我們一起來聊聊一個有趣的婚姻匹配問題。
這個問題是我學到的比較有趣的演算法問題前幾名了,也是當年我們ACM校隊面向新生宣講的時候選擇的例題。我們覺得用找物件這種新生會比較感興趣的問題來忽悠他們,他們上鉤的可能性比較大XD。
問題描述
婚姻匹配也可以叫做CP匹配,問題的場景非常簡單。我們模擬真實的婚戀匹配的場景,比如線下的N男 vs N女的相親活動。很自然的,男生和女生都會對異性在心裡有一個評價,覺得自己中意哪個討厭哪個,會有一個優先順序排名。
我們要做的事情就是設計一個演算法,將這N男和N女組成穩定的CP。因為如果是隨便組CP的話非常簡單,隨便配對就好了,但是隨便組成的CP並不一定和諧,很有可能不穩定,我們希望情侶們能夠快樂地生活在一起。

解釋一下穩定這個概念,我們假設男生有兩個,男1和男2,女生也有兩個女1和女2。假設我們組成的CP是男1和女2,男2和女1,但是呢,在女生當中,男1更喜歡女1,同樣在男生當中女1也更喜歡男1。
也就是說和自己的物件相比,他們對彼此的喜歡要大於各自的伴侶。那麼這種情況的CP就是不穩定的,時間長了有可能會出問題。為了簡化問題模型,我們假設一定會出問題,男1最終會和女1在一起,他們各自和自己現在的CP”分手“。
我們希望能夠把N男和N女組成CP,並且希望他們都不會分手,也就是說整個局面是穩定的。
問題的解法
關於這個問題,可能大家會有很多種想法,比如有些人會覺得應該給每個男生和女生根據受對方歡迎的情況打一個分。看看誰是被許多女生喜愛的優質男生,誰又是受男生歡迎的優質女生。
因為優質男生和優質女生受到對方的關注比較多,所以先把他們安排好,防止他們出現不穩定的情況。之後再去安排那些相對不那麼受歡迎的男女生。
這種方法看似可以,但是實現起來非常複雜,可行性不高,因為優質男女之間以及優質男女和非優質男女之間都有可能出現不穩定的情況。本質上關於避免不穩定情況出現的邏輯還是欠缺的。
我們還可以用搜索演算法來解,這個搜尋空間其實是明確的,就是男女生配對,我們就是要搜尋出一個穩定的配對情況。我們也可以用搜索問題來做,搜尋出所有的可能,然後一個一個篩選,找到其中穩定的解。
這種方法當然是可以的,但是複雜度非常高,因為我們絕大多數的搜尋情況是無效的。
有沒有效率既高又可以充分解決問題的方法呢?
當然也是有的,並且還非常簡單,就是讓這些男生根據自己心中的排名去追求女生。那麼就會出現多個男生同時或者先後追求同一名女生的情況,這裡我們做一個非常簡單的假設,假設女生始終會選擇在自己列表上排名高的那一個男生作為自己的CP。
第一輪我們讓所有的男生都去追求自己最心儀的女生,經過一系列競爭,必然會有一些男生成功的組成了CP。第二輪,我們讓單身的男生再去追求自己第二喜歡的女生,經過一輪競爭,又有一些人脫單了。我們如此迴圈往復,直到所有的人都配對。
這樣,我們的演算法就介紹完了。
就這麼簡單嗎?是的就這麼簡單,但是這樣能保證所有男女都能找到物件嗎?會不會有一些男女和女生剩下,或者是會出現不穩定的情況呢?
其實是不會的,證明也非常容易。
首先,可以證明不會出現有人沒有配對成功的情況。我們假設存在一男一女最後落單的情況,那麼假設的前提就是剩男已經向所有的女生都表過白並且被拒絕了。但女生在只有一個追求者的情況下是不會拒絕的,所以這就與假設矛盾了。所以演算法不會出現沒有結果的情況,可以保證所有男女都組成CP。
其次,我們可以證明不會出現男女不穩定的情況。我們也可以使用反證法,我們假設存在男1和女1彼此都是各自更加喜歡的,但是又沒有在一起。但是根據我們演算法的規則,那麼男1必然先於當前的物件追求女1。那麼對於女1來說,如果男1大於她當前的物件,她不可能不和男1在一起,所以這也是矛盾的。
到這裡,整個演算法的過程就介紹完了。這個演算法其實是有來頭的,並不是我們自己YY的,它的學名叫做Gale-Shapley演算法。顧名思義是由Gale和Shapley兩個人在1962年共同研究發表的,據說在該演算法發表的10年之前,美國一些地方就使用這個演算法來給醫學院的畢業生分配工作。可見在很早之前,人們就意識到了穩定匹配的重要性,並且依據直覺開始應用了。
演算法實現
這個演算法其實很容易實現,我們只需要記錄下面男生和女生當前的匹配情況,以及男生向女生髮起追求的輪次,中間的邏輯非常簡單。
女生如果單身,那麼一定接受男生的追求,否則比較一下和現在物件的優先順序。如果優先順序更高,後來的男生競爭上崗,前面的男生下崗,回到單身狀態。我們只需要把這些狀態釐清,程式碼實現非常簡單。我實現了一個版本,給大家提供一下參考:
import random
import sys
# 生產測試資料,生成男生和女生心中的物件排序
def generate_list(n):
base = list(range(n))
random.shuffle(base)
return base
if __name__ == "__main__":
boys, girls = [], []
n = int(sys.argv[1])
for i in range(n):
boys.append(generate_list(n))
girls.append(generate_list(n))
print('The preference of boys')
print(boys)
print('The preference of girls')
print(girls)
# 一開始的時候匹配狀態記為-1
girls_matched = [-1 for _ in range(n)]
# 男生髮起輪次記為0,表示下一次追求第幾偏好的女生
boys_round = [0 for _ in range(n)]
boys_matched = [-1 for _ in range(n)]
while True:
all_matched = True
for i in range(n):
# 如果已經匹配了,則跳過
if boys_matched[i] != -1:
continue
all_matched = False
girl = boys[i][boys_round[i]]
boys_round[i] += 1
# 如果女生沒有物件,直接答應
if girls_matched[girl] == -1:
girls_matched[girl] = i
boys_matched[i] = girl
else:
# 否則和現在物件比較一下順序
idx = girls[girl].index(i)
mate = girls_matched[girl]
mate_idx = girls[girl].index(mate)
if idx < mate_idx:
boys_matched[i] = girl
boys_matched[mate] = -1
girls_matched[girl] = i
if all_matched:
break
print('The match result of boys:')
print(boys_matched)
print('The match result of girls:')
print(girls_matched)
我們執行一下程式碼,檢視結果:
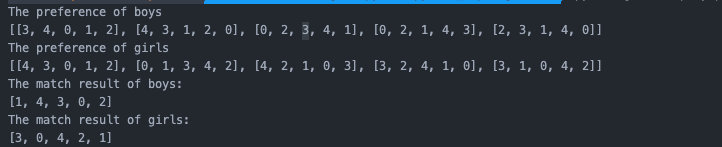
我們可以模擬一下,第一輪結果是[0-3], [1-4], [3-0], [4-2]。其中2和3號男生都向0號女生髮起追求,0號女生接受了3號拒絕了2號。於是第二輪2號男生向2號女生髮起追求,由於2號女已經和最佳心儀物件4號男組成了CP,所以2號男失敗。繼續向3號女發起追求,3號女的原來物件是0號男,由於0號男排名非常低,於是0號男被甩。所以第二輪的結果是[1-4],[2-3],[3-0],[4-2]。
第二輪的結果是0號男落下,0號男向4號以及0號女發起追求都宣告失敗,最終和1號女組成CP。所有的男女都組成了CP,並且沒有不穩定的情況出現。我們人工推理得到的結果和我們程式給出的結果完全一致。
總結
這個演算法並不難,但是勝在非常有趣。實際上在生活當中有許多分配方案直接或者是間接使用了Gale-Shapley演算法。如果大家熟悉演算法的話,會發現其實這個問題的本質是二分圖匹配。我們可以用二分圖匹配的演算法來解決這個問題。
如果我們研究一下這個演算法的核心邏輯,會發現其實是對男生有優勢的,雖然女生看起來有最終的選擇權,但男生更有機會追求自己最心儀的物件,而女生只能被動地等待男生髮起追求來進行挑選。如果某個女生喜歡的男生不選她,那麼她永遠沒有和他在一起的機會。這個故事告訴我們,喜歡的物件要自己挑,主動才是王道。
如果你還單身的話,希望對你有所幫助。
今天的文章到這裡就結束了,如果喜歡本文的話,請來一波素質三連,給我一點支援吧(關注、在看、點贊)。
