# 貝塞爾曲線 ## bezierCurveTo 線上工具 https://canvature.appspot.com/ [感覺這個好用一些] https://blogs.sitepointstatic.com/examples/tech/canvas-curves/bezier-curve.html 三次貝塞爾曲線必須包含三個點。前兩個點`（cp1x，cp1y）`和`（cp2x，cp2y）`是在三次貝塞爾曲線計算中使用的控制點，最後一個點`（x，y）`是曲線的終點。 `bezierCurveTo（cp1x，cp1y，cp2x，cp2y，x，y）` | 參量 | 型別 | 描述 | | :--- | :----- | :---------------------------- | | cp1x | number | 第一個貝塞爾控制點的x座標。 | | cp1y | number | 第一個貝塞爾控制點的y座標。 | | cp2x | number | 第二個貝塞爾控制點的x座標。 | | cp2y | number | 第二個貝塞爾控制點的y座標。 | | X | number | 要新增到當前路徑的點的x座標。 | | y | number | 要新增到當前路徑的點的y座標。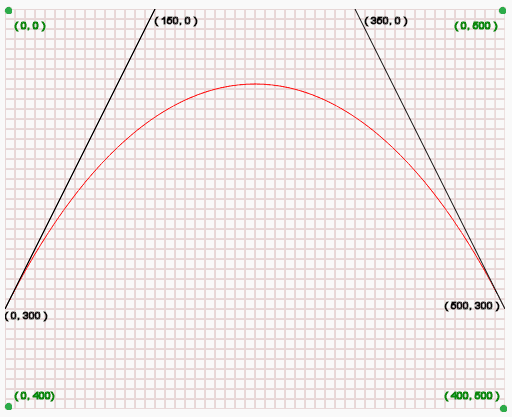 |  - （0，300）是曲線的起點。[這個用`moveTo(x,y)`嘆氣的點] - （150，0）即（cp1x，cp1y）是曲線的第一個控制位置。 - （350，0）即（cp2x，cp2y）是曲線的第二個控制位置。 - （500，300），即（x，y）是曲線的終點。 ## quadraticCurveTo 二次貝塞爾曲線,需要兩個點,控制點和曲線的終點  - （0，300）是曲線的起點。 - （250，0）即（cp1x，cp1y）是曲線的控制位置。 - （500，300），即（x，y）是曲線的終點。 ## 繪製視覺化的二次貝塞爾曲線demo 初始化 ```html

code

``` ```js let canvas = document.querySelector('#canvas') // 程式碼文字 let code = document.querySelector('#code'); let ctx = canvas.getContext('2d'), point, style = {// 原點樣式 radius: 10, width: 2, color: '#900', fill: 'rgba(200,200,200,.5)', arc1: 0, arc2: 2 * Math.PI }, drag = null,// 按下的時候 確認滑鼠拿的那一個點 dPoint, // 拿到當前點的座標 cpline = { width: 1, color: 'red' }, curve = { width: 6, color: '#333' } // 初始化預設資料 function init() { point = {// 滑鼠的三個點 p1: { // moveTo x: 100, y: 50 }, cp1: { // 貝塞爾第一個點 x: 100, y: 200 }, p2: {// 貝塞爾第二個點 x: 300, y: 200 } } } // 程式碼文字 function showCode() { if (code) { code.firstChild.nodeValue = "theCanvas = document.getElementById(\"canvas\");\n" + "ctx = theCanvas.getContext(\"2d\")\n" + "ctx.lineWidth = " + curve.width + ";\nctx.strokeStyle = \"" + curve.color + "\";\nctx.beginPath();\n" + "ctx.moveTo(" + point.p1.x + ", " + point.p1.y + ");\n" + "ctx.quadraticCurveTo(" + point.cp1.x + ", " + point.cp1.y + ", " + point.p2.x + ", " + point.p2.y + ");" + "\nctx.stroke();" ; } } ``` 畫出頁面 ```js function drawScreen() { // 清空畫布 ctx.clearRect(0, 0, canvas.width, canvas.height) ctx.lineCap = 'round'; ctx.lineJoin = 'round'; ctx.lineWidth = cpline.width; ctx.strokeStyle = cpline.color; ctx.beginPath() ctx.moveTo(point.p1.x, point.p1.y) ctx.lineTo(point.cp1.x, point.cp1.y) ctx.lineTo(point.p2.x, point.p2.y) ctx.stroke(); //中間的弧度 ctx.lineWidth = curve.width; ctx.strokeStyle = curve.color; ctx.beginPath(); ctx.moveTo(point.p1.x, point.p1.y) ctx.quadraticCurveTo(point.cp1.x, point.cp1.y, point.p2.x, point.p2.y) ctx.stroke(); // 三個原點 for (let p in point) { console.log(p); ctx.lineWidth = style.width; ctx.strokeStyle = style.color; ctx.fillStyle = style.fill; ctx.beginPath(); ctx.arc(point[p].x, point[p].y, style.radius, style.arc1, style.arc2, true) ctx.fill(); ctx.stroke(); } showCode() } ``` 拿到滑鼠的滑鼠 ```js // 滑鼠的座標 function MousePos(event) { event = event ? event : window.event; return { x: event.pageX - canvas.offsetLeft, y: event.pageY - canvas.offsetTop } } ``` 問個來了,當我們滑鼠移動的時候怎麼確定滑鼠放在圓裡面啦 這裡又運用了初中數學知識**圓的標準方程**  ```js canvas.addEventListener('mousedown', dragStart, false); canvas.addEventListener('mousemove', dragging, false); canvas.addEventListener('mouseup', dragEnd, false); canvas.addEventListener('mouseout', dragEnd, false); ``` 這裡我們需要知道點應該在圓內 ```js 滑鼠按下的時候 function dragStart(e) { e = MousePos(e) let dx, dy; // 找到滑鼠拿到哪一個點 for (let p in point) { dx = point[p].x - e.x; dy = point[p].y - e.y; if ((dx ** 2) + (dy ** 2) < style.radius ** 2) { // 確定了拿到那個點 drag = p; // 確定了拿到點的滑鼠 dPoint=e; canvas.style.cursor = 'move'; return; } } } ``` 滑鼠移動 ```js function dragging(e) { // 這個是用來判斷有按下的引數的時候觸發 if (drag) { e = MousePos(e); // 滑鼠的x - 開始滑鼠的點 point[drag].x += e.x - dPoint.x; point[drag].y += e.y - dPoint.y; dPoint = e; drawScreen(); } } ``` 滑鼠離開 ```js function dragEnd(e) { drag = null; canvas.style.cursor = 'default'; drawScreen(); } ``` ## 再二次貝塞爾曲線的基礎上繪製三次貝塞爾曲線 修改1,給`html`新增一個class ```js ``` 在初始化資料的時候,新增第二個點 ```js // 初始化預設資料,預設不傳引數三次貝塞爾曲線,不預設二次 function init(quadratic) { .... if (quadratic) { point.cp1={ x:250,y:100 } }else{ point.cp1={ x:150,y:100 } point.cp2={ x:350,y:100 } } ``` 畫出螢幕的時候 ```js function drawScreen() { ... ctx.lineTo(point.cp1.x, point.cp1.y) // 判斷是否有第二個點 if (point.cp2) { ctx.moveTo(point.p2.x,point.p2.y) ctx.lineTo(point.cp2.x,point.cp2.y) }else{ ctx.lineTo(point.p2.x, point.p2.y); } ... ctx.moveTo(point.p1.x, point.p1.y) // 確認二次還是三次 if (point.cp2) { ctx.bezierCurveTo(point.cp1.x, point.cp1.y, point.cp2.x, point.cp2.y, point.p2.x, point.p2.y) }else{ ctx.quadraticCurveTo(point.cp1.x, point.cp1.y, point.p2.x, point.p2.y); } ... } ``` 修改程式碼顯示的部分 ```js +(point.cp2 ? "ctx.bezierCurveTo("+point.cp1.x+", "+point.cp1.y+", "+point.cp2.x+", "+point.cp2.y+", "+point.p2.x+", "+point.p2.y+");" : "ctx.quadraticCurveTo("+point.cp1.x+", "+point.cp1.y+", "+point.p2.x+", "+point.p2.y+");" )