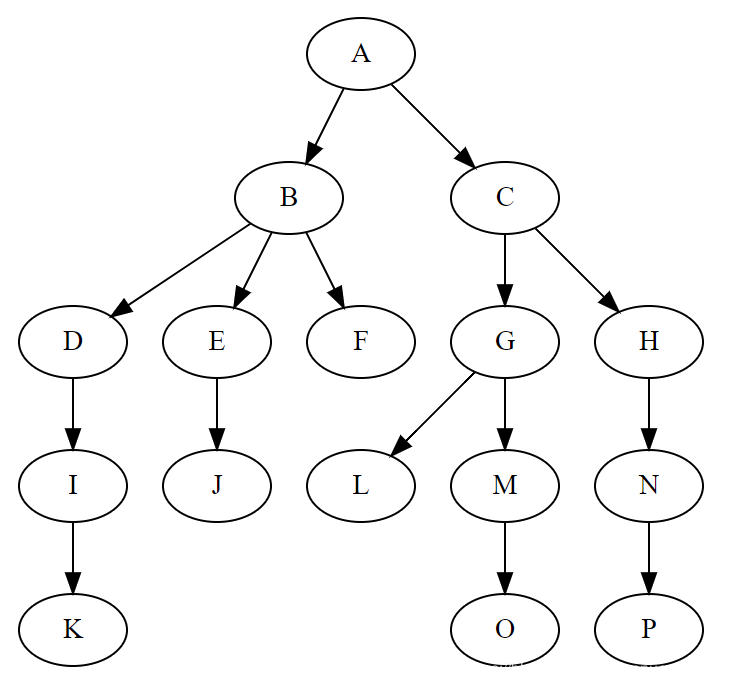
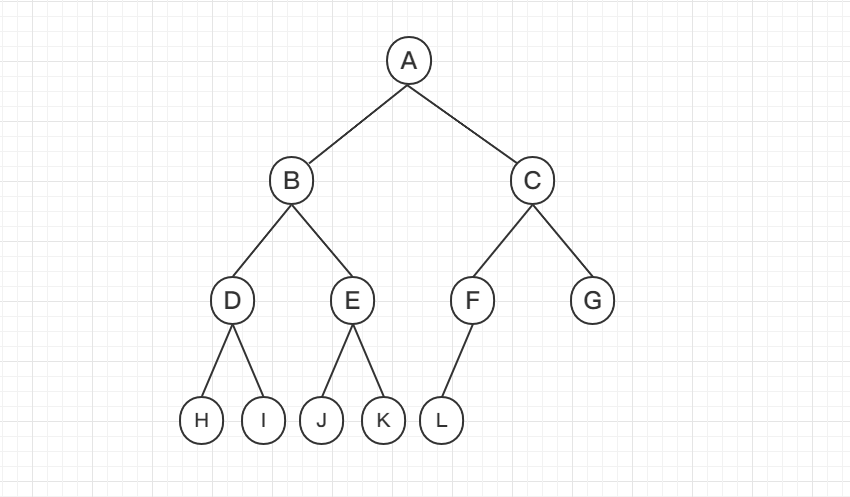
# 樹的結構 樹（tree）是一種抽象資料型別或是實現這種抽象資料型別的資料結構，用來模擬具有樹狀結構性質的資料集合 它具有以下的特點： ①每個節點有零個或多個子節點； ②沒有父節點的節點稱為根節點； ③每一個非根節點有且只有一個父節點； ④除了根節點外，每個子節點可以分為多個不相交的子樹；  # 樹的分類 ## 二叉樹 二叉樹：每個節點最多含有兩個子樹的樹稱為二叉樹。  二叉樹中一些專業術語： - 父節點：A節點就是B節點的父節點，B節點是A節點的子節點 - 兄弟節點：B、C這兩個節點的父節點是同一個節點，所以他們互稱為兄弟節點 - 根節點：A節點沒有父節點，我們把沒有父節點的節點叫做根節點 - 葉子節點：圖中的H、I、J、K、L節點沒有子節點，我們把沒有子節點的節點叫做葉子節點 - `節點的高度`：節點到葉子結點的最長路徑，比如C節點的高度是2（L->F是1，F->C是2) - `節點的深度`：節點到根節點的所經歷的邊的個數比如C節點的高度是1（A->C，只有一條邊，所以深度=1） - `節點的層`：節點的高度 - `樹的高度`：根節點的高度 基於二叉樹衍生的多種樹型結構： ## 滿二叉樹 `滿二叉樹`：除最後一層無任何子節點外，每一層上的所有結點都有兩個子結點。也可以這樣理解，除葉子結點外的所有結點均有兩個子結點。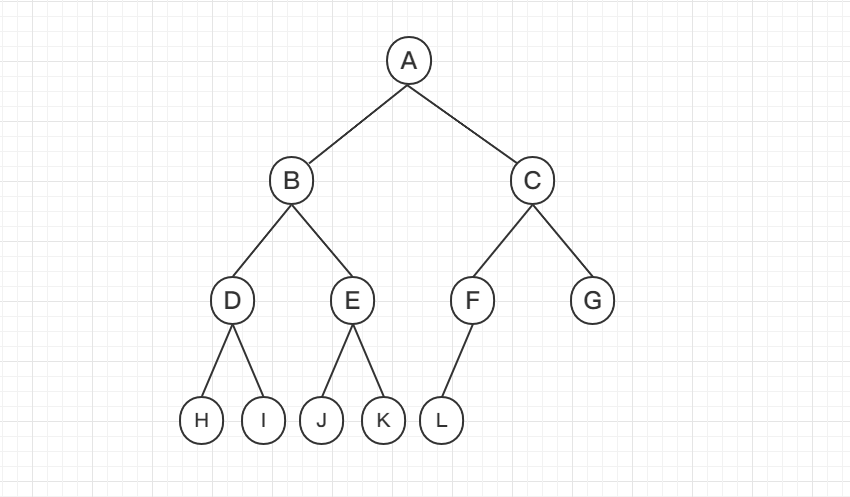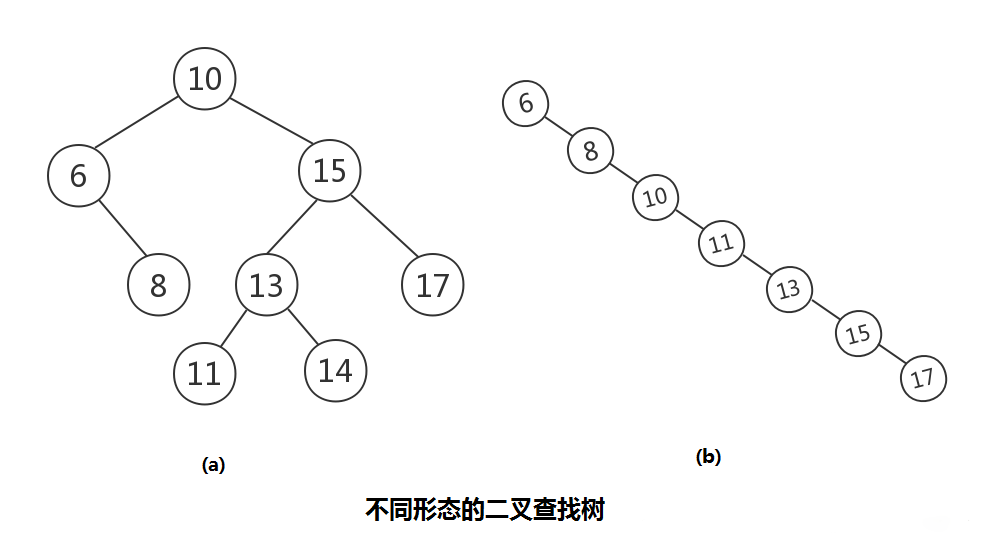節點數達到最大值，所有葉子結點必須在同一層上  ## 完全二叉樹 `完全二叉樹`：設二叉樹的深度為h，除第 h 層外，其它各層 (1～h-1) 的結點數都達到最大個數，第h 層所有的結點都連續集中在最左邊，這就是完全二叉樹  滿二叉樹和完全二叉樹對比：  ## 二叉查詢樹 `二叉查詢樹`: 也稱二叉搜尋樹，或二叉排序樹。其定義也比較簡單，要麼是一顆空樹，要麼就是具有如下性質的二叉樹： （1）若任意節點的左子樹不空，則左子樹上所有結點的值均小於它的根結點的值； （2） 若任意節點的右子樹不空，則右子樹上所有結點的值均大於它的根結點的值； （3） 任意節點的左、右子樹也分別為二叉查詢樹； （4） 沒有鍵值相等的節點。  ## 平衡二叉樹 `定義`: 平衡二叉搜尋樹，又被稱為AVL樹，且具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹 `平衡二叉樹出現原因`: 由於普通的二叉查詢樹會容易失去”平衡“，極端情況下，二叉查詢樹會退化成線性的連結串列，導致插入和查詢的複雜度下降到 O(n) ，所以，這也是平衡二叉樹設計的初衷。那麼平衡二叉樹如何保持”平衡“呢？根據定義，有兩個重點，一是左右兩子樹的高度差的絕對值不能超過1，二是左右兩子樹也是一顆平衡二叉樹。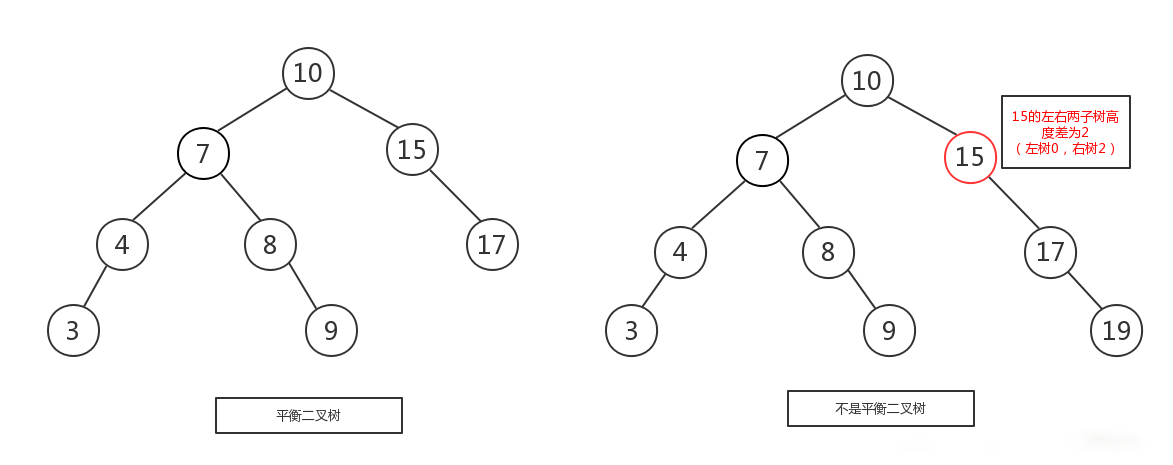  `平衡二叉樹的建立`: 平衡二叉樹是一棵高度平衡的二叉查詢樹。所以，要構建跟維繫一棵平衡二叉樹就比普通的二叉樹要複雜的多。在構建一棵平衡二叉樹的過程中，當有新的節點要插入時，檢查是否因插入後而破壞了樹的平衡，如果是，則需要做旋轉去改變樹的結構 ## 紅黑樹 avl樹每次插入刪除會進行大量的平衡度計算導致IO數量巨大而影響效能。所以出現了紅黑樹。一種二叉查詢樹，但在每個節點增加一個儲存位表示節點的顏色，可以是紅或黑（非紅即黑）  `定義`: 1. 每個節點非紅即黑; 2. 根節點是黑的; 3. 每個葉節點（葉節點即樹尾端NULL指標或NULL節點）都是黑的; 4. 如圖所示，如果一個節點是紅的，那麼它的兩兒子都是黑的; 5. 對於任意節點而言，其到葉子點樹NULL指標的每條路徑都包含相同數目的黑節點; 6. 每條路徑都包含相同的黑節點; 紅黑樹有兩個`重要性質`： 1、紅節點的孩子節點不能是紅節點； 2、從根到葉子節點的任意一條路徑上的黑節點數目一樣多。 這兩條性質確保該樹的高度為logN，所以是平衡樹。 `優勢`： 紅黑樹的查詢效能略微遜色於AVL樹，因為他比avl樹會稍微不平衡最多一層，也就是說紅黑樹的查詢效能只比相同內容的avl樹最多多一次比較，但是，紅黑樹在插入和刪除上完爆avl樹，avl樹每次插入刪除會進行大量的平衡度計算，而紅黑樹為了維持紅黑性質所做的紅黑變換和旋轉的開銷，相較於avl樹為了維持平衡的開銷要小得多 `使用場景`： 1. 廣泛用於C ++的STL中，地圖和集都是用紅黑樹實現的; 2. 著名的Linux的的程序排程完全公平排程程式，用紅黑樹管理程序控制塊，程序的虛擬記憶體區域都儲存在一顆紅黑樹上，每個虛擬地址區域都對應紅黑樹的一個節點，左指標指向相鄰的地址虛擬儲存區域，右指標指向相鄰的高地址虛擬地址空間; 3. IO多路複用的epoll的的的實現採用紅黑樹組織管理的的的sockfd，以支援快速的增刪改查; 4. Nginx的的的中用紅黑樹管理定時器，因為紅黑樹是有序的，可以很快的得到距離當前最小的定時器; 5. Java的的的中TreeMap中的中的實現; ## B樹 `定義`： B樹是為實現高效的磁碟存取而設計的`多叉`平衡搜尋樹。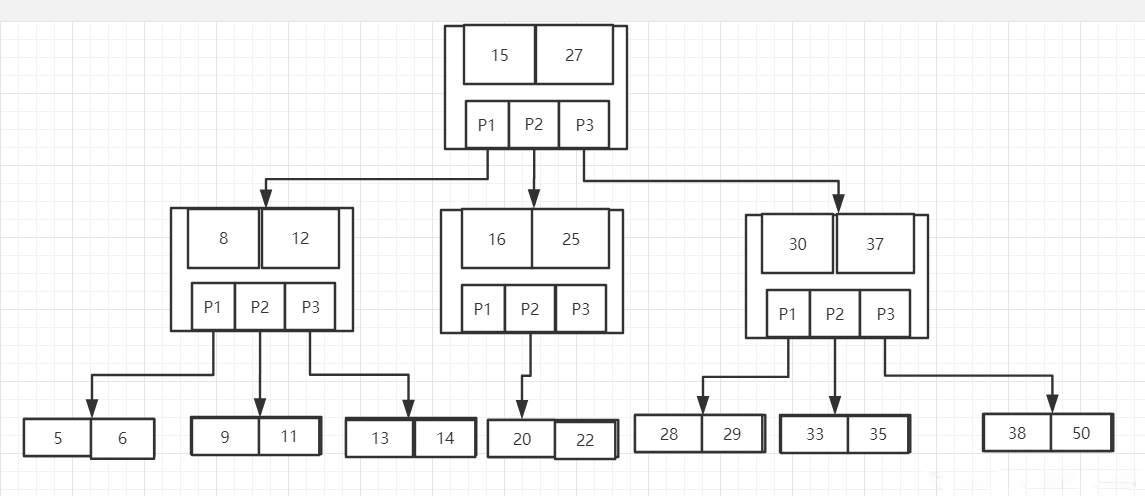（B樹和B-tree這兩個是同一種樹）  `產生原因`： B樹是一種查詢樹，我們知道，這一類樹（比如二叉查詢樹，紅黑樹等等）最初生成的目的都是為了解決某種系統中，查詢效率低的問題。 B樹也是如此，它最初啟發於二叉查詢樹，二叉查詢樹的特點是每個非葉節點都只有兩個孩子節點。然而這種做法會導致當`資料量非常大時，二叉查詢樹的深度過深`，搜尋演算法自根節點向下搜尋時，需要訪問的節點也就變的相當多。 如果這些節點儲存在外儲存器中，每訪問一個節點，相當於就是進行了一次I/O操作，隨著樹高度的增加，頻繁的I/O操作一定會降低查詢的效率。 `定義`: B樹是一種平衡的多分樹，通常我們說m階的B樹，它必須滿足如下條件： 1. 每個節點最多隻有m個子節點。 2. 每個非葉子節點（除了根）具有至少⌈ m/2⌉子節點。 3. 如果根不是葉節點，則根至少有兩個子節點。 4. 具有k個子節點的非葉節點包含k -1個鍵。 5. `所有葉子都出現在同一水平`，沒有任何資訊（高度一致）。 `特點`: 1. 關鍵字集合分佈在整棵樹中； 2. 多路，非二叉樹 3. 每個節點既儲存索引，又儲存資料 4. 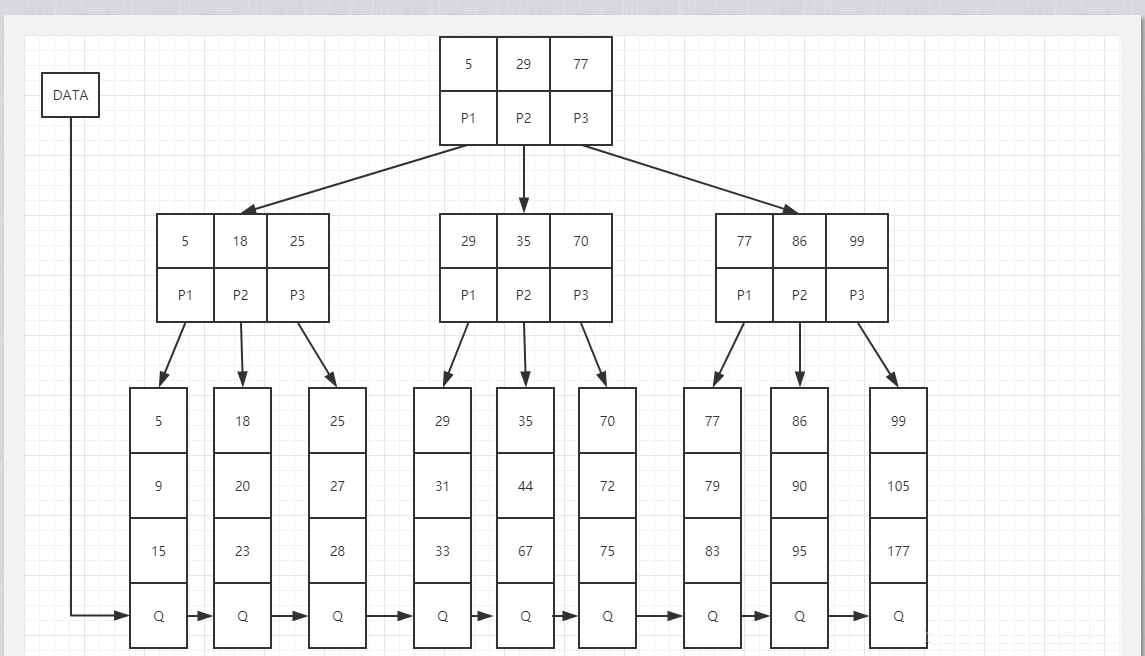搜尋時相當於二分查詢 ## B+樹 B+樹是應檔案系統所需而產生的B樹的變形樹  B+樹有兩種型別的節點：內部結點（也稱索引結點）和葉子結點。內部節點就是非葉子節點，內部節點不儲存資料，只儲存索引，資料都儲存在葉子節點。 內部結點中的key都按照從小到大的順序排列，對於內部結點中的一個key，左樹中的所有key都小於它，右子樹中的key都大於等於它。葉子結點中的記錄也按照key的大小排列。 每個葉子結點都存有相鄰葉子結點的指標，葉子結點本身依關鍵字的大小自小而大順序連結 父節點存有右孩子的第一個元素的索引。 最核心的特點如下： （1）多路非二叉 （2）只有葉子節點儲存資料 （3）搜尋時相當於二分查詢 （4）增加了相鄰接點的指向指標 `B+樹為什麼時候做資料庫索引`：由於B+樹的資料都儲存在葉子結點中，分支結點均為索引，方便掃庫，只需要掃一遍葉子結點即可，但是B樹因為其分支結點同樣儲存著資料，我們要找到具體的資料，需要進行一次中序遍歷按序來掃。簡單來說就是：B+樹查詢某一個數據時掃描葉子節點即可；而B樹需要中序遍歷整個樹，所以B+樹更快。 `為什麼說B+樹比B樹更適合資料庫索引？` 1）B+樹的磁碟讀寫代價更低 　　B+樹的內部結點並沒有指向關鍵字具體資訊的指標。因此其內部結點相對B 樹更小。如果把所有同一內部結點的關鍵字存放在同一盤塊中，那麼盤塊所能容納的關鍵字數量也越多。一次性讀入記憶體中的需要查詢的關鍵字也就越多。相對來說IO讀寫次數也就降低了； 2）B+樹查詢效率更加穩定 　　由於非終結點並不是最終指向檔案內容的結點，而只是葉子結點中關鍵字的索引。所以任何關鍵字的查詢必須走一條從根結點到葉子結點的路。所有關鍵字查詢的路徑長度相同，導致每一個數據的查詢效率相當； 3）B+樹便於範圍查詢（最重要的原因，範圍查詢是資料庫的常態） 　　B樹在提高了IO效能的同時並沒有解決元素遍歷效率低下的問題，正是為了解決這個問題，B+樹應用而生。B+樹只需要去遍歷葉子節點就可以實現整棵樹的遍歷。而且在資料庫中基於範圍的查詢是非常頻繁的，而B樹不支援這樣的操作或者說效率太低； B樹的範圍查詢用的是中序遍歷，而B+樹用的是在連結串列上遍歷； # 樹的建立 樹的建立有很多種方式，分為迭代建立和遞迴建立。下面分別介紹這兩種建立數的方式。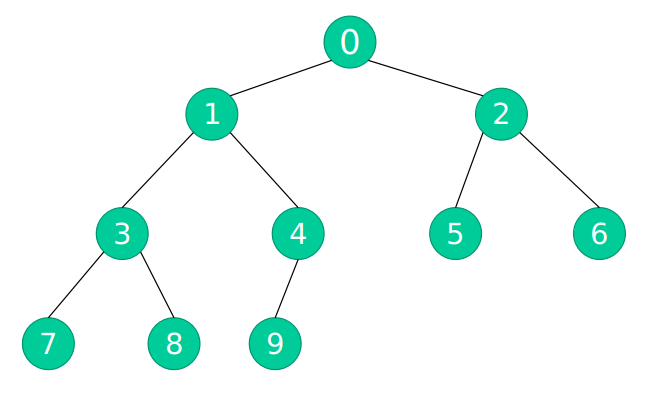 ## 迭代建立 建立的樹：  該建立方法是按照層次建立，第一層建立好之後第二層，第二層完成後建立第三層。 ```python class Node(object): def __init__(self,value=-1,left=None,right=None): self.value = value self.left = left self.right = right class Tree(object): def __init__(self, root=None): self.root = root def insert(self,element): node = Node(element) if self.root == None: self.root = node else: queue = [] queue.append(self.root) while queue: cur = queue.pop(0) if cur.left == None: cur.left = node return elif cur.right == None: cur.right = node return else: queue.append(cur.left) queue.append(cur.right) def output(self, root): if root == None: return print(root.value) self.output(root.left) self.output(root.right) one = Tree() for i in range(10): one.insert(i) one.output(one.root) ``` ## 遞迴建立 該建立方式是遞迴建立，前提是將樹的資料組織成一個完全二叉樹的形式 ``` class Node(object): def __init__(self,value=None): self.value = value self.left = None self.right = None def create_two(index, length, arr): if index > length: return None node = Node(arr[index]) node.left = create_two(index*2+1, length, arr) node.right = create_two(index*2+2, length, arr) return node def BFS(root): queue = [root] while queue: cur = queue.pop(0) print(cur.value) if cur.left: queue.append(cur.left) if cur.right: queue.append(cur.right) arr = [1,2,3,4,None,None,None,None,None] length = len(arr) -1 head = create_two(0,length, arr) print(head.value) print(head.left) print(head.right) BFS(head) ``` # 樹的遍歷 樹的遍歷方式有很多種，可以分為五類： 1. 前序遍歷 2. 中序遍歷 3. 後序遍歷 4. 層次遍歷 5. 子樹遍歷 實現遍歷的方式中有可以分為遞迴和迭代 ``` class TreeNode(object): def __init__(self,value=None): self.value = value self.left = None self.right = None class Tree(object): def __init__(self): self.root = TreeNode(None) self.arr = [] def create(self,value): if self.root.value is None: self.root = TreeNode(value) else: queue = [self.root] while queue: node = queue.pop(0) if node.left: queue.append(node.left) else: node.left = TreeNode(value) return if node.right: queue.append(node.right) else: node.right = TreeNode(value) return # 遞迴、前序遍歷 def preorder(self,root): if root is None: return self.arr.append(root.value) self.preorder(root.left) self.preorder(root.right) # 遞迴、中序遍歷 def inorder(self,root): if root is None: return self.inorder(root.left) self.arr.append(root.value) self.inorder(root.right) # 遞迴、後序遍歷 def postorder(self,root): if root is None: return self.postorder(root.left) self.postorder(root.right) self.arr.append(root.value) # 迭代、前序遍歷 def preorder_two(self,root): stack = [root] arr = [] while stack: cur = stack.pop() arr.append(cur.value) if cur.right: stack.append(cur.right) if cur.left: stack.append(cur.left) print(arr) # 迭代、後序遍歷 def postorder_two(self,root): stack = [root] arr = [] while stack: cur = stack.pop() arr.append(cur.value) if cur.left: stack.append(cur.left) if cur.right: stack.append(cur.right) print(arr[::-1]) # 迭代、中序遍歷 def inorder_two(self,root): cur = root stack = [] arr = [] while cur or stack: while cur: stack.append(cur) cur = cur.left node = stack.pop() arr.append(node.value) cur = node.right print(arr) # 層次遍歷 def levelorder(self,root): queue = [root] arr = [] while queue: cur = queue.pop(0) arr.append(cur.value) if cur.left: queue.append(cur.left) if cur.right: queue.append(cur.right) print(arr) # 子數遍歷，返回從根節點到每一個葉子節點的一條路徑 # 子數遍歷，返回從根節點到每一個葉子節點的一條路徑 def zishu(self,root,arr): if not root.left and not root.right: print(arr) return if root.left: self.zishu(root.left, arr + [root.left.value]) if root.right: self.zishu(root.right, arr + [root.right.value]) tree = Tree() for i in range(10): tree.create(i) print('--------------------遞迴--------------------------') tree.preorder(tree.root) print(tree.arr) tree.arr = [] tree.inorder(tree.root) print(tree.arr) tree.arr = [] tree.postorder(tree.root) print(tree.arr) print('--------------------迭代--------------------------') tree.preorder_two(tree.root) tree.inorder_two(tree.root) tree.postorder_two(tree.root) print('--------------------層次--------------------------') tree.levelorder(tree.root) print('--------------------子數--------------------------') tree.arr = [] tree.zishu(tree.root, [tree.root.value]) print(tree.arr) ``` ![](https://img2020.cnblogs.com/blog/1060878/202012/1060878-20201207104842077-5833155