說到儲存結構,我們就會想到常用的兩種儲存方式:順序儲存和鏈式儲存兩種。

先來看看順序儲存，用一段地址連續的儲存單元依次儲存線性表中資料元素，這對於線性表來說是很自然的，但是對於樹這種一對多的結構而言是否適合呢？

樹中某個結點的孩子可以有多個，這就意味著，無論用哪種順序將樹中所有的結點儲存到陣列中，結點的儲存位置都無法直接反映邏輯關係，試想一下，資料元素挨個儲存，那麼誰是誰的雙親，誰是誰的孩子呢？所以簡單的順序儲存是不能滿足樹的實現要求的。

不過可以充分利用順序儲存和鏈式儲存結構的特點，完全可以實現對樹的儲存結構的表示。

下面介紹三種不同的樹的表示法:雙親表示法,、孩子表示法,、孩子兄弟表示法。

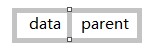
1、雙親表示法：

     我們假設以一組連續空間儲存樹的結點，同時在每個結點中，附設一個指示器指向其雙親結點到連結串列中的位置。也就是說每個結點除了知道自己之外還需要知道它的雙親在哪裡。

它的結構特點是如圖所示：            

以下是我們的雙親表示法的結構定義程式碼：

/*樹的雙親表示法結點結構定義  */
#define MAXSIZE 100
typedef int ElemType;		//樹結點的資料型別，暫定為整形 
typedef struct PTNode		//結點結構
{
	ElemType data;			//結點資料
	int parent;				//雙親位置
}PTNode;

typedef struct
{
	PTNode nodes[MAXSIZE];	//結點陣列
	int r,n;				//根的位置和結點數
}PTree;
 

2、孩子表示法

換一種不同的考慮方法。由於每個結點可能有多棵子樹，可以考慮使用多重連結串列，即每個結點有多個指標域，其中每個指標指向一棵子樹的根結點，我們把這種方法叫做多重連結串列表示法。不過樹的每個結點的度，也就是它的孩子個數是不同的。所以可以設計兩種方案來解決。

方案一：

一種是指標域的個數就等於樹的度（樹的度是樹的各個結點度的最大值）

其結構如圖所示：

不過這種結構由於每個結點的孩子數目不同，當差異較大時，很多結點的指標域就都為空，顯然是浪費空間的，不過若樹的各結點度相差很小時，那就意味著開闢的空間都被利用了，這時這種缺點反而變成了優點。

方案二：

第二種方案是每個結點指標域的個數等於該結點的度，我們專門取一個位置來儲存結點指標域的個數。

其結構如圖所示：

這種方法克服了浪費空間的缺點，對空間的利用率是很高了，但是由於各個結點的連結串列是不相同的結構，加上要維護結點的度的數值，在運算上就會帶來時間上的損耗。

能否有更好的方法呢，既可以減少空指標的浪費，又能是結點結構相同。

說到這大家肯定就知道是有的麥，那就是孩子表示法。

具體辦法是，把每個結點的孩子排列起來，以單鏈表做儲存結構，則n個結點有n個孩子連結串列，如果是葉子結點則此單鏈表為空。然後n個頭指標有組成一個線性表，採用順序儲存結構，存放進入一個一維陣列中。

為此，設計兩種結點結構，

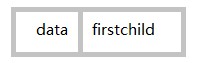
一個是孩子連結串列的孩子結點，如下所示：

其中child是資料域，用來儲存某個結點在表頭陣列中的下標。next是指標域，用來儲存指向某結點的下一個孩子結點的指標。

另一個是表頭結點，如下所示：

其中data是資料域，儲存某結點的資料資訊。firstchild是頭指標域，儲存該結點的孩子連結串列的頭指標。

以下是孩子表示法的結構定義程式碼：

/*樹的孩子表示法結點結構定義  */
#define MAXSIZE 100
typedef int ElemType;		//樹結點的資料型別，暫定為整形 
typedef struct CTNode		//孩子結點
{
	int child;
	struct CTNode *next;
}*ChildPtr;

typedef struct				//表頭結構
{
	ElemType data;
	ChildPtr firstchild;
}CTBox;
typedef struct				//樹結構
{
	CTBox nodes[MAXSIZE];	//結點陣列
	int r,n;				//根結點的位置和結點數
}CTree;

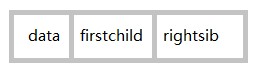
我們發現，任意一顆樹，它的結點的第一個孩子如果存在就是的，它的右兄弟如果存在也是唯一的。因此，我們設定兩個指標，分別指向該結點的第一個孩子和此結點的右兄弟。

其結點結構如圖所示：

以下是孩子兄弟表示法的結構定義程式碼：

/*樹的孩子兄弟表示法結構定義 */
typedef struct CSNode
{
	ElemType  data;
	struct CSNode  *firstchild, *rightsib;
}CSNode, *CSTree;