# 數獨生成及求解方案剖析（Java實現） ## **關鍵詞** - 數獨9x9 - 數獨生成 - 數獨解題 --- ## **序言** 最近業務在鞏固Java基礎，編寫了一個基於JavaFX的數獨小遊戲（隨後放連結）。寫到核心部分發現平時玩的數獨這個東西，還真有點意思： **行、列、子宮格**之間的數字互相影響，牽一髮而動全身，一不留神就碰撞衝突了,簡直都能搞出玄學的意味，怪不得古人能由此“[九宮格](https://baike.baidu.com/item/%E4%B9%9D%E5%AE%AB%E6%A0%BC/2216215)”演繹出八卦和《周易》。 於是自己想了不少演算法，也查找了不少資料，但是都沒有找到理想的Java實現；最後無意間在Github發現一個國外大佬寫了這樣一個演算法，體味一番，頓覺精闢！ 本篇就是把國外大佬的這個演算法拿過來，進行一個深入的解析，希望能幫助到用得上的人。 --- ## **正文** 先上地址 數獨演算法Github地址：https://github.com/a11n/sudoku 數獨演算法Github中文註解地址：https://github.com/JobsLeeGeek/sudoku 程式碼只有三個類： - Generator.java > 生成器 -> 生成數獨格子 - Solver.java > 解法器 -> 數獨求解 - Grid.java > 網格物件 -> 基礎數獨格子物件 直接上main方法看下基本呼叫： ```java public static void main(String[] args) { // 生成一個20個空格的9x9數獨 Generator generator = new Generator(); Grid grid = generator.generate(20); System.out.println(grid.toString()); // 9x9數獨求解 Solver solver = new Solver(); solver.solve(grid); System.out.println(grid.toString()); } ``` 看下輸出結果（輸出方法我自己進行了修改）： 生成的9x9數獨（0為空格） ``` [9, 8, 0, 1, 0, 2, 5, 3, 7] [1, 4, 2, 5, 0, 7, 9, 8, 6] [0, 3, 7, 0, 8, 0, 1, 0, 0] [8, 9, 1, 0, 2, 4, 3, 0, 5] [6, 2, 0, 0, 0, 5, 8, 0, 0] [3, 7, 0, 8, 9, 1, 6, 2, 4] [4, 6, 9, 2, 1, 8, 7, 5, 3] [2, 1, 8, 0, 0, 0, 4, 6, 9] [0, 5, 3, 4, 6, 9, 2, 1, 8] ``` 數獨求解 ``` [9, 8, 6, 1, 4, 2, 5, 3, 7] [1, 4, 2, 5, 3, 7, 9, 8, 6] [5, 3, 7, 9, 8, 6, 1, 4, 2] [8, 9, 1, 6, 2, 4, 3, 7, 5] [6, 2, 4, 3, 7, 5, 8, 9, 1] [3, 7, 0, 8, 9, 1, 6, 2, 4] [4, 6, 9, 2, 1, 8, 7, 5, 3] [2, 1, 8, 7, 5, 3, 4, 6, 9] [7, 5, 3, 4, 6, 9, 2, 1, 8] ``` 使用起來很簡單，速度也很快；其核心部分的程式碼，其實只有三個點。 ### 1. 第一點 解法 - 隨機陣列 - 遞迴填數 在Solver.java中solve方法實現； 每次遍歷的是使用交換方法實現的隨機陣列，保證了隨機陣列空間的有限佔用，並且能夠減少列舉過程中的重複機率。 程式碼我已經做了中文註釋： ```java /** * 獲取隨機陣列 * * @return */ private int[] generateRandomValues() { // 初始化隨機陣列 此處空格子0是因為格子初始化的時候 預設給的就是0 便於判斷和處理 int[] values = {EMPTY, 1, 2, 3, 4, 5, 6, 7, 8, 9}; Random random = new Random(); // 使用交換法構建隨機陣列 for (int i = 0, j = random.nextInt(9), tmp = values[j]; i < values.length; i++, j = random.nextInt(9), tmp = values[j]) { if (i == j) continue; values[j] = values[i]; values[i] = tmp; } return values; } /** * 求解方法 * * @param grid * @param cell * @return */ private boolean solve(Grid grid, Optional cell) { // 空格子 說明遍歷處理完了 if (!cell.isPresent()) { return true; } // 遍歷隨機數值 嘗試填數 for (int value : values) { // 校驗填的數是否合理 合理的話嘗試下一個空格子 if (grid.isValidValueForCell(cell.get(), value)) { cell.get().setValue(value); // 遞迴嘗試下一個空格子 if (solve(grid, grid.getNextEmptyCellOf(cell.get()))) return true; // 嘗試失敗格子的填入0 繼續為當前格子嘗試下一個隨機值 cell.get().setValue(EMPTY); } } return false; } ``` ### 2. 第二點 構建 - 物件陣列 整個物件的構建在Grid.java中，其中涉及到兩個物件Grid和Cell，Grid由Cell[][]陣列構成，Cell中記錄了格子的數值、行列子宮格維度的格子列表及下一個格子物件： Grid物件 ```java /** * 由資料格子構成的數獨格子 */ private final Cell[][] grid; ``` Cell物件 ```java // 格子數值 private int value; // 行其他格子列表 private Collection rowNeighbors; // 列其他格子列表 private Collection columnNeighbors; // 子宮格其他格子列表 private Collection boxNeighbors; // 下一個格子物件 private Cell nextCell; ``` ### 3. 第三點 遍歷判斷 - 多維度引用 - 判斷重複 Grid初始化時，在Cell物件中，使用List構造了行、列、子宮格維度的**引用**（請注意這裡的引用，後面會講到這個引用的妙處），見如下程式碼及中文註釋： ```java /** * 返回數獨格子的工廠方法 * * @param grid * @return */ public static Grid of(int[][] grid) { ... // 初始化格子各維度統計List 9x9 行 列 子宮格 Cell[][] cells = new Cell[9][9]; List> rows = new ArrayList<>(); List> columns = new ArrayList<>(); List> boxes = new ArrayList<>(); // 初始化List 9行 9列 9子宮格 for (int i = 0; i < 9; i++) { rows.add(new ArrayList()); columns.add(new ArrayList()); boxes.add(new ArrayList()); } Cell lastCell = null; // 逐一遍歷數獨格子 往各維度統計List中填數 for (int row = 0; row < grid.length; row++) { for (int column = 0; column < grid[row].length; column++) { Cell cell = new Cell(grid[row][column]); cells[row][column] = cell; rows.get(row).add(cell); columns.get(column).add(cell); // 子宮格在List中的index計算 boxes.get((row / 3) * 3 + column / 3).add(cell); // 如果有上一次遍歷的格子 則當前格子為上個格子的下一格子 if (lastCell != null) { lastCell.setNextCell(cell); } // 記錄上一次遍歷的格子 lastCell = cell; } } // 逐行 逐列 逐子宮格 遍歷 處理對應模組的關聯鄰居List for (int i = 0; i < 9; i++) { // 逐行 List row = rows.get(i); for (Cell cell : row) { List rowNeighbors = new ArrayList<>(row); rowNeighbors.remove(cell); cell.setRowNeighbors(rowNeighbors); } // 逐列 ... // 逐子宮格 ... } ... } ``` 構造完成後，每試一次填數，就遍歷一次多維度的List判斷行、列、3x3子宮格的數字是否重複： ```java /** * 判斷格子填入的數字是否合適 * * @param cell * @param value * @return */ public boolean isValidValueForCell(Cell cell, int value) { return isValidInRow(cell, value) && isValidInColumn(cell, value) && isValidInBox(cell, value); } ... /** * 判斷數獨行數字是否合規 * * @param cell * @param value * @return */ private boolean isValidInRow(Cell cell, int value) { return !getRowValuesOf(cell).contains(value); } ... /** * 獲取行格子數值列表 * * @param cell * @return */ private Collection getRowValuesOf(Cell cell) { List rowValues = new ArrayList<>(); for (Cell neighbor : cell.getRowNeighbors()) rowValues.add(neighbor.getValue()); return rowValues; } ``` --- 看完程式碼，其實不難發現，演算法不是很複雜，簡潔易懂——通過隨機和遞迴進行列舉和試錯，外加List.contains()方法遍歷判斷；邏輯並不複雜，程式碼也十分精煉； 於是本人通過使用基本資料int[][]，不使用物件，按照其核心邏輯實現了自己的一套數獨，卻發現極度耗時（大家可以自己嘗試下），很久沒有結果輸出。 為什麼同樣是遞迴，自己的效能卻這麼差呢？ 仔細思考，最後發現**面向物件**真的是個好東西，例子中的**物件的引用**從很大一層面上解決了本方法數獨遞迴的效能問題。 --- 寫一個有趣的例子來解釋下，用一個物件構建二維陣列，初始化數值後，分別按照行維度和列維度關聯到對應的List中，列印陣列和這些List； 然後我們修改(0,0)位置的數值，**注意，這裡不是new一個新的物件，而是直接使用物件的set方法操作其對應數值**，再列印陣列和這些List，程式碼和結果如下： 示例程式碼 ```java public static void main(String[] args) { Entity[][] ee = new Entity[3][3]; for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { Entity e = new Entity(); e.setX(i); e.setY(j); ee[i][j] = e; } } System.out.println(Arrays.deepToString(ee)); List> row = new ArrayList<>(); List> column = new ArrayList<>(); for (int i = 0; i < 3; i++) { row.add(new ArrayList<>()); } for (int i = 0; i < 3; i++) { for (int j = 0; j < 3; j++) { row.get(i).add(ee[i][j]); } } for (int j = 0; j < 3; j++) { column.add(new ArrayList<>()); } for (int j = 0; j < 3; j++) { for (int i = 0; i < 3; i++) { column.get(j).add(ee[i][j]); } } System.out.println(row); System.out.println(column); System.out.println(""); ee[0][0].setX(9); ee[0][0].setY(9); System.out.println(Arrays.deepToString(ee)); System.out.println(row); System.out.println(column); } static class Entity { private int x; private int y; public int getX() { return x; } public void setX(int x) { this.x = x; } public int getY() { return y; } public void setY(int y) { this.y = y; } @Override public String toString() { return "Entity{" + "x=" + x + ", y=" + y + '}'; } } ``` 輸出結果 ``` [[Entity{x=0, y=0}, Entity{x=0, y=1}, Entity{x=0, y=2}], [Entity{x=1, y=0}, Entity{x=1, y=1}, Entity{x=1, y=2}], [Entity{x=2, y=0}, Entity{x=2, y=1}, Entity{x=2, y=2}]] [[Entity{x=0, y=0}, Entity{x=0, y=1}, Entity{x=0, y=2}], [Entity{x=1, y=0}, Entity{x=1, y=1}, Entity{x=1, y=2}], [Entity{x=2, y=0}, Entity{x=2, y=1}, Entity{x=2, y=2}]] [[Entity{x=0, y=0}, Entity{x=1, y=0}, Entity{x=2, y=0}], [Entity{x=0, y=1}, Entity{x=1, y=1}, Entity{x=2, y=1}], [Entity{x=0, y=2}, Entity{x=1, y=2}, Entity{x=2, y=2}]] [[Entity{x=9, y=9}, Entity{x=0, y=1}, Entity{x=0, y=2}], [Entity{x=1, y=0}, Entity{x=1, y=1}, Entity{x=1, y=2}], [Entity{x=2, y=0}, Entity{x=2, y=1}, Entity{x=2, y=2}]] [[Entity{x=9, y=9}, Entity{x=0, y=1}, Entity{x=0, y=2}], [Entity{x=1, y=0}, Entity{x=1, y=1}, Entity{x=1, y=2}], [Entity{x=2, y=0}, Entity{x=2, y=1}, Entity{x=2, y=2}]] [[Entity{x=9, y=9}, Entity{x=1, y=0}, Entity{x=2, y=0}], [Entity{x=0, y=1}, Entity{x=1, y=1}, Entity{x=2, y=1}], [Entity{x=0, y=2}, Entity{x=1, y=2}, Entity{x=2, y=2}]] ``` 神奇的地方就在這裡，行列關聯的List裡面的數值跟隨著一起改變了。 這是為什麼呢？ > Java的集合中存放的型別 > > （1）如果是基本資料型別，則是value； > > （2） 如果是複合資料型別，則是引用的地址； List中放入物件時，實際放入的不是物件本身而是物件的引用； 物件陣列只需要自己佔據一部分記憶體空間，List來引用物件，就不需要額外有陣列記憶體的開支； 同時對原始陣列中物件的修改（注意，修改並非new一個物件，因為new一個就開闢了新的記憶體地址，引用還會指向原來的地址），就可以做到**遍歷一次、處處可見**了！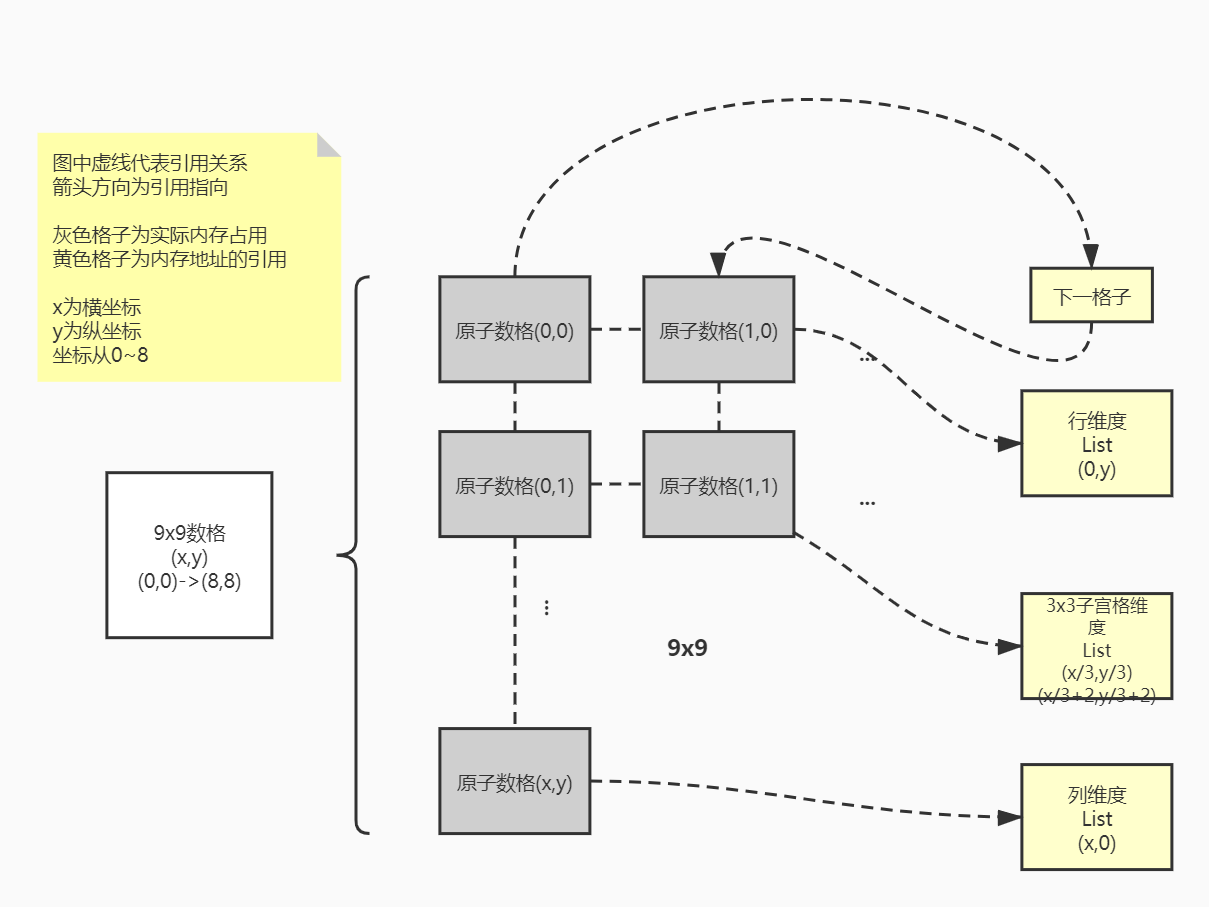 --- 由此畫一張實體與引用關係圖：  這樣以來，陣列記憶體還是原來的一塊陣列記憶體，我們只需用List關聯引用，就不用需要每次遍歷和判斷的時候開闢額外空間了； 然後每次對原始數格處理的時候，其各個維度List都不用手動再去修改；每次對各個維度數字進行判斷的時候，也就都是在對原始數格進行遍歷；其**空間複雜度**沒有增加。 --- ## **總結** 1. 使用**遞迴+隨機陣列**進行列舉和試錯——邏輯簡明高效 2. 使用**List+物件**構建數獨格子（行、列、3x3子宮格）各維度關聯 3. 使用List遍歷和排查重複——方法呼叫簡單，**引用**完美控制了空間複雜度 **分析到此，與其說是演算法，不如說是對Java物件的構建，通過對Java物件的有效構建，來高效、簡便的完成了一次數獨的生成和求解。** 這便是面向物件程式碼構建的獨到之處！ 妙哉