轉載請註明出處：

原理

退火的物理含義概述

模擬退火演算法來源於固體退火原理，在熱力學上，退火（annealing）現象指物體逐漸降溫的物理現象，溫度愈低，物體的能量狀態會低；夠低後，液體開始冷凝與結晶，在結晶狀態時，系統的能量狀態最低。大自然在緩慢降溫（亦即，退火）時，可“找到”最低能量狀態：結晶。但是，如果過程過急過快，快速降溫（亦稱「淬鍊」，quenching）時，會導致不是最低能態的非晶形。

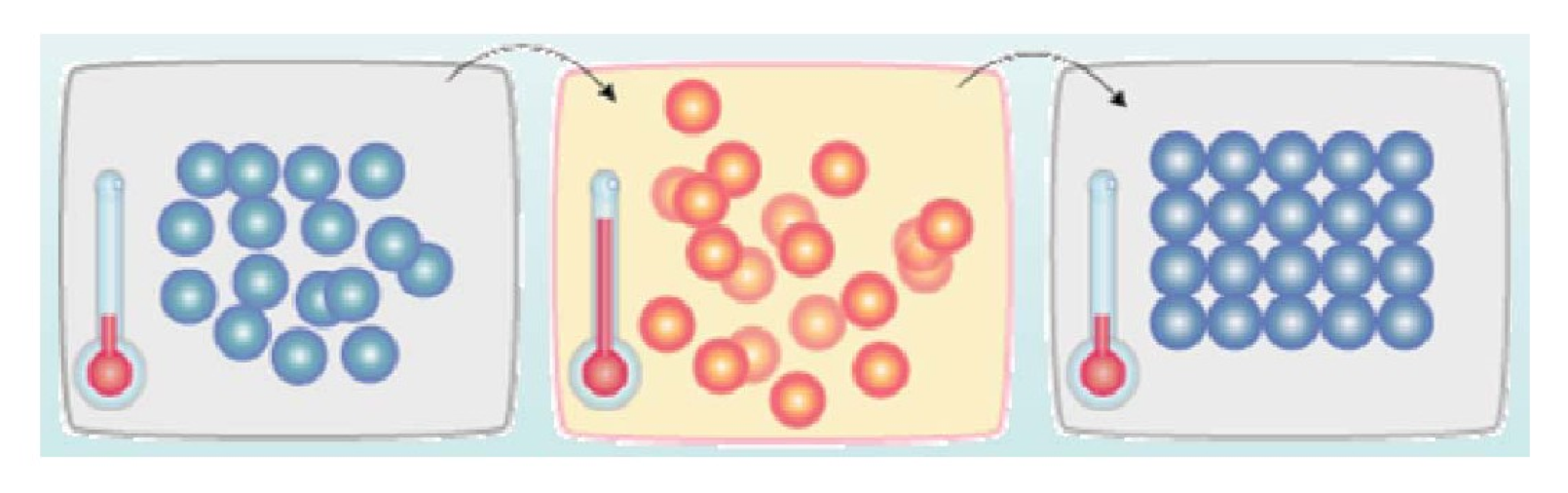
如下圖所示，首先（左圖）物體處於非晶體狀態。我們將固體加溫至充分高（中圖），再讓其徐徐冷卻，也就退火（右圖）。加溫時，固體內部粒子隨溫升變為無序狀，內能增大，而徐徐冷卻時粒子漸趨有序，在每個溫度都達到平衡態，最後在常溫時達到基態，內能減為最小（此時物體以晶體形態呈現）。

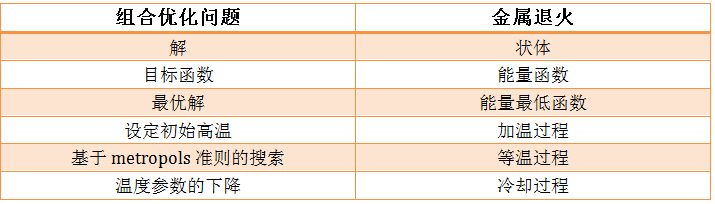
組合優化問題與金屬退火的類比

本演算法適用的組合最優化問題建模

組合最優化問題包含如下要素：

1.定義域：x∈D，D為所有狀態的空間，x為某一狀態
2.目標函式 : f(x);
3.約束方程：g(x)≥0;
4.最優解z=min{f(x)| g(x)≥0, x∈D };

模擬退火演算法流程：

step1：先設定好初始溫度t0=最高溫度tMax, 隨機選定一個初始狀態i，計算f(i)；
step2：若在當前溫度下達到內層迴圈的退出條件，則轉step3執行；否則，從鄰域N(i)中隨機選擇一個狀態j, 並計算出exp((f(i) - f(j))/temperature)，
若exp((f(i) - f(j))/temperature)>random(0, 1), 則重複執行step2;
step3: 若溫度t滿足退出條件，則轉step2執行；

模擬退火演算法虛擬碼：

/*
* J(y)：在狀態y時的評價函式值
* Y(i)：表示當前狀態
* Y(i+1)：表示新的狀態
* r： 用於控制降溫的快慢
* T： 系統的溫度，系統初始應該要處於一個高溫的狀態
* T_min ：溫度的下限，若溫度T達到T_min，則停止搜尋
*/
while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ; 

　　if ( dE >=0 ) //表達移動後得到更優解，則總是接受移動
       Y(i+1) = Y(i) ; //接受從Y(i)到Y(i+1)的移動
　　else
　　{
       // 函式exp( dE/T )的取值範圍是(0,1) ，dE/T越大，則exp( dE/T )也
 

       if ( exp( dE/T ) > random( 0 , 1 ) )
           Y(i+1) = Y(i) ; //接受從Y(i)到Y(i+1)的移動
　　}
　　    T = r * T ; //降溫退火 ，0<r<1 。r越大，降溫越慢；r越小，降溫越快
　　/*
　　* 若r過大，則搜尋到全域性最優解的可能會較高，但搜尋的過程也就較長。若r過小，則搜尋的過程會很快，但最終可能會達到一個區域性最優值
　　*/
　　i ++ ;
}

模擬退火演算法數學模型：

模擬退火演算法數學模型可以描述為，在給定結構後，模擬退火過程是從一個狀態到另一狀態的隨機遊動：

應用於求解TSP問題及Java實現

TSP問題建模

TSP問題（Travelling Salesman Problem）即旅行商問題，又譯為旅行推銷員問題、貨郎擔問題，是數學領域中著名問題之一。假設有一個旅行商人要拜訪n個城市，他必須選擇所要走的路徑，路徑的限制是每個城市只能拜訪一次，而且最後要回到原來出發的城市。路徑的選擇目標是要求得的路徑路程為所有路徑之中的最小值。

TSP問題是一個組合優化問題。該問題可以被證明具有NPC計算複雜性。TSP問題可以分為兩類，一類是對稱TSP問題（Symmetric TSP），另一類是非對稱問題（Asymmetric TSP）。所有的TSP問題都可以用一個圖（Graph）來描述：

V={c1, c2, …, ci, …, cn}，i = 1,2, …, n，是所有城市的集合.ci表示第i個城市，n為城市的數目；

E={(r, s): r,s∈ V}是所有城市之間連線的集合；

C = {crs: r,s∈ V}是所有城市之間連線的成本度量（一般為城市之間的距離）；

如果crs = csr, 那麼該TSP問題為對稱的，否則為非對稱的。

一個TSP問題可以表達為：

求解遍歷圖G = (V, E, C)，所有的節點一次並且回到起始節點，使得連線這些節點的路徑成本最低。

Java版實現的原始碼

1.建立City類,用於對要去的各個城市建模；

City.java

public class City {
    int x;
    int y;

    // Constructs a randomly placed city
    public City(){
        this.x = (int)(Math.random()*200);
        this.y = (int)(Math.random()*200);
    }

    // Constructs a city at chosen x, y location
    public City(int x, int y){
        this.x = x;
        this.y = y;
    }

    // Gets city's x coordinate
    public int getX(){
        return this.x;
    }

    // Gets city's y coordinate
    public int getY(){
        return this.y;
    }

    // Gets the distance to given city
    public double distanceTo(City city){
        int xDistance = Math.abs(getX() - city.getX());
        int yDistance = Math.abs(getY() - city.getY());
        double distance = Math.sqrt( (xDistance*xDistance) + (yDistance*yDistance) );
        return distance;
    }

    @Override
    public String toString(){
        return getX()+", "+getY();
    }
}

2.建立Tour類，對旅行路線進行建模；

Tour.java

public class Tour {
    /** Holds our citiesList of cities*/
    private ArrayList<City> citiesList ; // Cache
    private int distance = 0;

    public Tour() {
        // TODO Auto-generated constructor stub
        citiesList = new ArrayList<City>();
    }


    /** 
     * Constructs a citiesList from another citiesList
     * */
    public Tour(ArrayList<City> tour){
        citiesList = new ArrayList<City>();
        for (City city : tour) {
            this.citiesList.add(city);
        }

    }

    /** Returns citiesList information*/
    public ArrayList<City> getCitiesList(){
        return citiesList;
    }

    /** Creates a random individual*/
    public Tour generateIndividual() {
        // Loop through all our destination cities and add them to our citiesList
        for (int cityIndex = 0; cityIndex < citiesList.size(); cityIndex++) {
          setCity(cityIndex, this.getCity(cityIndex));
        }
        // Randomly reorder the citiesList
        Collections.shuffle(citiesList);
        return this;
    }

    /**Create new neighbour tour*/
    public Tour generateNeighourTour(){
        Tour newSolution = new Tour(this.citiesList);
        // Get a random positions in the tour
        int tourPos1 = (int) (newSolution.numberOfCities() * Math
                .random());
        int tourPos2 = (int) (newSolution.numberOfCities() * Math
                .random());
        // Get the cities at selected positions in the tour
        City citySwap1 = newSolution.getCity(tourPos1);
        City citySwap2 = newSolution.getCity(tourPos2);

        // Swap them
        newSolution.setCity(tourPos2, citySwap1);
        newSolution.setCity(tourPos1, citySwap2);
        return newSolution;
    }

    /** Gets a city from the citiesList*/
    public City getCity(int tourPosition) {
        return (City)citiesList.get(tourPosition);
    }

    /** Sets a city in a certain position within a citiesList*/
    public void setCity(int tourPosition, City city) {
        citiesList.set(tourPosition, city);
        // If the tours been altered we need to reset the fitness and distance
        distance = 0;
    }

    public Tour addCity(City city) {
        citiesList.add(city);
        return this;
    }

    public ArrayList<City> getAllCities() {
        return citiesList;
    }

    /** Gets the total distance of the citiesList*/
    public int getDistance(){
        if (distance == 0) {
            int tourDistance = 0;
            // Loop through our citiesList's cities
            for (int cityIndex=0; cityIndex < numberOfCities(); cityIndex++) {
                // Get city we're traveling from
                City fromCity = getCity(cityIndex);
                // City we're traveling to
                City destinationCity;
                // Check we're not on our citiesList's last city, if we are set our
                // citiesList's final destination city to our starting city
                if(cityIndex+1 < numberOfCities()){
                    destinationCity = getCity(cityIndex+1);
                }
                else{
                    destinationCity = getCity(0);
                }
                // Get the distance between the two cities
                tourDistance += fromCity.distanceTo(destinationCity);
            }
            distance = tourDistance;
        }
        return distance;
    }

    /** Get number of cities on our citiesList*/
    public int numberOfCities() {
        return citiesList.size();
    }

    @Override
    public String toString() {
        String geneString = "|";
        for (int i = 0; i < numberOfCities(); i++) {
            geneString += getCity(i)+"|";
        }
        return geneString;
    }
}

3.關鍵演算法實現部分；

simulated annealing.java

public class SimulatedAnnealing {

    /**Set initial temp*/
    private double currentTemperature = 5000;
    /**minimal temperature to cool*/
    private double minTemperature = 0.0001;
    private double internalLoop = 1000;
    /**Cooling rate*/
    private double coolingRate = 0.001;
    /** Initialize intial solution*/
    private Tour currentSolution ;

    /**
     * set a random initial tour
     * 
     * */
    public void initTour() {
        Tour tour = new Tour();
        tour.addCity(new City(60, 200))
            .addCity(new City(180, 200))
            .addCity(new City(80, 180))
            .addCity(new City(140, 180))
            .addCity(new City(20, 160))
            .addCity(new City(100, 160))
            .addCity(new City(200, 160))
            .addCity(new City(140, 140))
            .addCity(new City(40, 120))
            .addCity(new City(100, 120))
            .addCity(new City(180, 100))
            .addCity(new City(60, 80))
            .addCity(new City(120, 80))
            .addCity(new City(180, 60))
            .addCity(new City(20, 40))
            .addCity(new City(100, 40))
            .addCity(new City(200, 40))
            .addCity(new City(20, 20))
            .addCity(new City(60, 20))
            .addCity(new City(160, 20));
        currentSolution = tour.generateIndividual();
        System.out.println("Initial solution distance: " + currentSolution.getDistance());
    }

    /**
     * iterate for getting the best Tour
     * @return best tour
     * */
    public Tour anneal() {
        DynamicDataWindow ddWindow=new DynamicDataWindow("模擬退火演算法收斂過程");
        ddWindow.setY_Coordinate_Name("所有路徑和 ");
        ddWindow.setVisible(true);
        long tp=0;

        Tour bestSolution = new Tour(currentSolution.getCitiesList());
        Tour newSolution = null;
        // Loop until system has cooled
        while (currentTemperature > minTemperature) {
            for (int i = 0; i < internalLoop; i++) {
                //get a solution from neighbour
                newSolution=currentSolution.generateNeighourTour();
                // Get energy of solutions
                int currentEnergy = currentSolution.getDistance();
                int neighbourEnergy = newSolution.getDistance();

                // Decide if we should accept the neighbour
                if (acceptanceProbability(currentEnergy, neighbourEnergy,
                        currentTemperature) > Math.random()) {
                    currentSolution = new Tour(newSolution.getCitiesList());
                }

                // Keep track of the best solution found
                if (currentSolution.getDistance() < bestSolution.getDistance()) {
                    bestSolution = new Tour(currentSolution.getCitiesList());
                }
            }
            // Cool system
            currentTemperature *= 1-coolingRate;

            long millis=System.currentTimeMillis();
            if (millis-tp>300) {
                tp=millis;
                ddWindow.addData(millis, bestSolution.getDistance());
            }
            try {
                Thread.sleep(10L);
            } catch (InterruptedException e) {
                e.printStackTrace();
            }
        }
        return bestSolution;
    }

    /**
     * 
     *  Calculate the acceptance probability
     **/
    private double acceptanceProbability(int energy, int newEnergy, double temperature) {
        // If the new solution is better, accept it
        if (newEnergy < energy) {
            return 1.0;
        }
        // If the new solution is worse, calculate an acceptance probability
        return Math.exp((energy - newEnergy) / temperature);
    }

    public static void main(String[] args) {
        SimulatedAnnealing sa=new SimulatedAnnealing();
        sa.initTour();
        Tour besTour = sa.anneal();
        System.out.println("Final solution distance: " +besTour.getDistance());
        System.out.println("Tour: " + besTour);
    }
}

4.執行過程視覺化顯示程式碼這裡就不再貼出了，有需要的可以去這裡下載完整原始碼工程

執行結果分析

執行截圖冷卻速率（即溫度下降的變化率）設定為0.001時，路徑大小收斂過程如下圖：

>
>
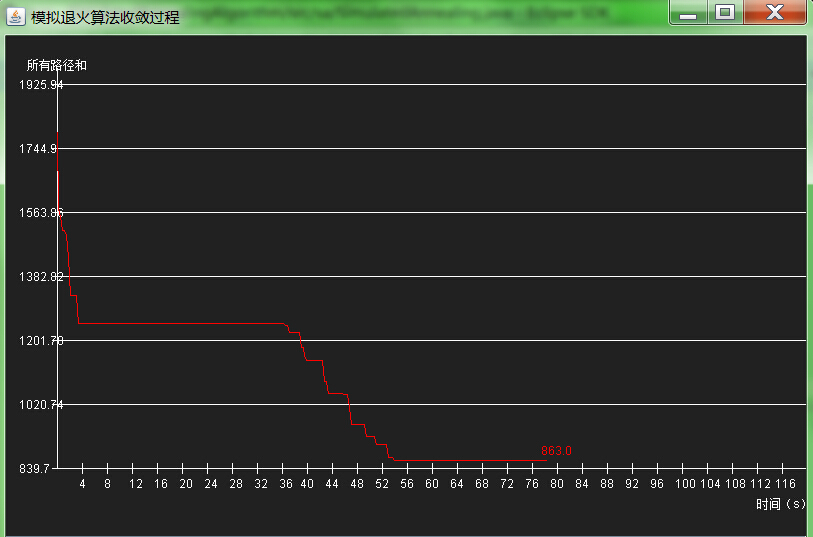
執行截圖冷卻速率（即溫度下降的變化率）設定為0.01時，路徑大小收斂過程如下圖：

>
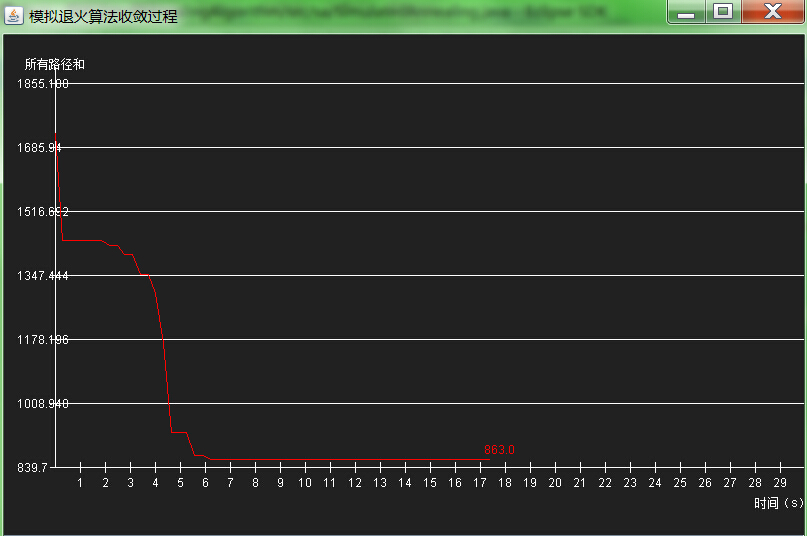
由上圖對比可以發現，冷卻速率越大，路徑大小收斂越快。但是，也不是說冷卻速率越大越好，冷卻速率越大越容易陷入區域性最優解。使用中，冷卻速率和內迴圈次數應綜合考慮。

總結

模擬退火演算法其特點是在開始搜尋階段解的質量提高比較緩慢，但是到了迭代後期，它的解的質量提高明顯，所以如果在求解過程中，對迭代步數限制比較嚴格的話，模擬退火演算法在有限的迭代步數內很難得到高質量的解。總體而言模擬退火演算法比較適合用於有充足計算資源的問題求解。

附上本文的全部原始碼：專案原始碼

參考資料