分別使用 Python 和 Math.Net 呼叫優化演算法
阿新 • • 發佈:2021-01-19
## 1. Rosenbrock 函式
在數學最優化中,Rosenbrock 函式是一個用來測試最優化演算法效能的非凸函式,由Howard Harry Rosenbrock 在 1960 年提出 。也稱為 Rosenbrock 山谷或 Rosenbrock 香蕉函式,也簡稱為香蕉函式。
Rosenbrock 函式的定義如下:
input)
{
return Math.Pow((1 - input[0]), 2) + 100 * Math.Pow((input[1] - input[0] * input[0]), 2);
}
var obj = ObjectiveFunction.Value(Value);
var solver = new NelderMeadSimplex(convergenceTolerance: 0.0000000001, maximumIterations: 1000);
var initialGuess = new DenseVector(new[] { 1.2, 1.2 });
var result = solver.FindMinimum(obj, initialGuess);
Console.WriteLine("Value:\t" + result.FunctionInfoAtMinimum.Value);
Console.WriteLine("Point:\t" + result.MinimizingPoint[0] + " , " + result.MinimizingPoint[1]);
Console.WriteLine("Iterations:\t" + result.Iterations);
```
輸出如下:
```
Value: 5.352382362443507E-19
Point: 1.0000000007114838 , 1.0000000014059296
Iterations: 145
```
雖然 `MathNet.Numerics.Optimization` 名稱空間下還提供了其它類,例如 BfgsBMinimizer 和 NewtonMinimizer,但它們還需要開發者提供梯度函式,這對我來說太複雜了,反而不如 NelderMeadSimplex 好用。
## 4. 最後
[Math.Net](https://www.mathdotnet.com/) 提供了很多多元函式區域性最小值的演算法,但比起 Python 還是簡化了太多,例如我還搞不清楚 [Math.Net](https://www.mathdotnet.com/) 中的優化演算法怎麼新增約束條件,這方面有機會再研究
f(x)=100(y−x^2^)^2^+(1−x)^2^
Rosenbrock 函式的每個等高線大致呈拋物線形,其全域最小值也位在拋物線形的山谷中(香蕉型山谷)。很容易找到這個山谷,但由於山谷內的值變化不大,要找到全域的最小值相當困難。
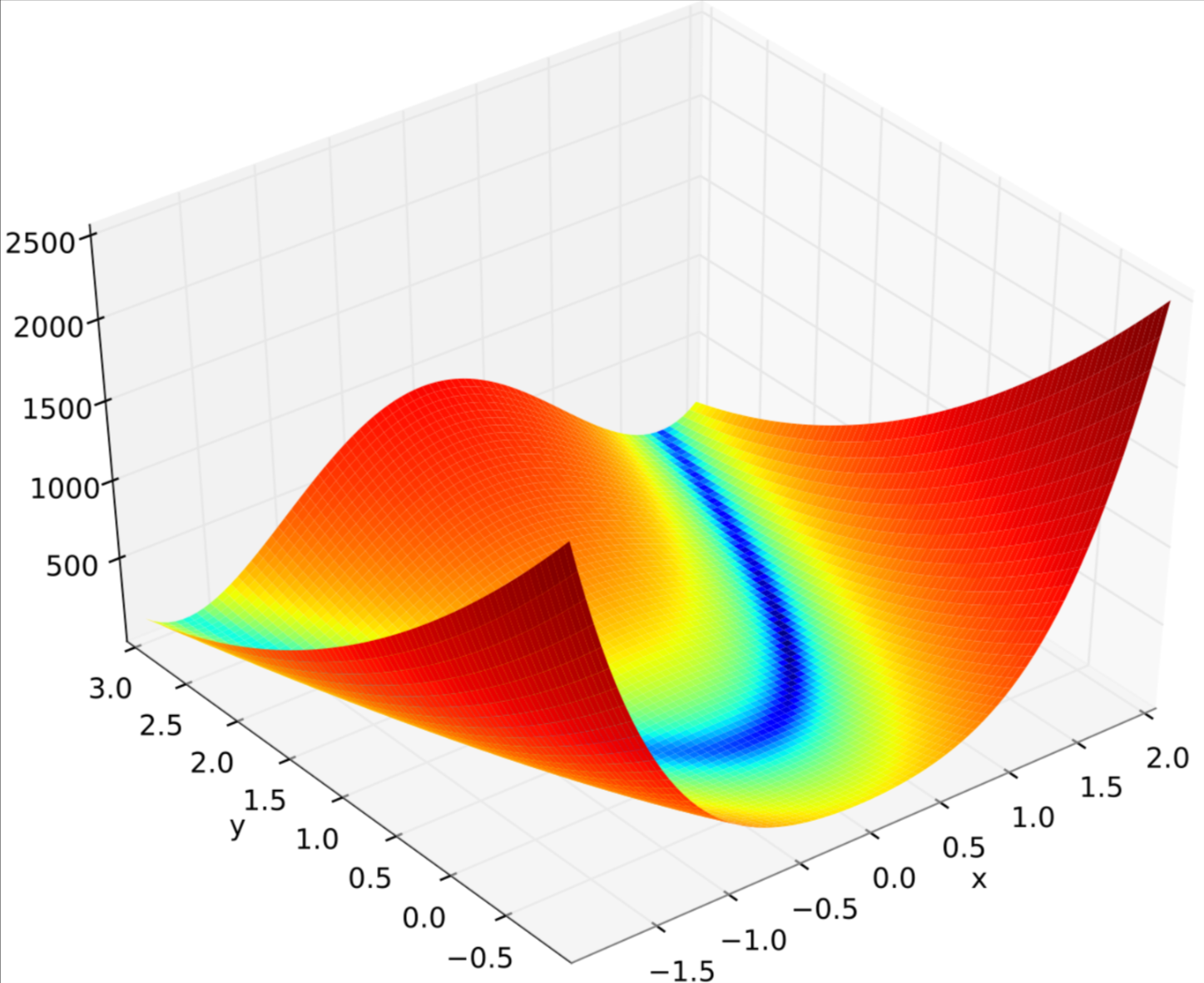
這篇文章分別用 Python 和 [Math.Net](https://www.mathdotnet.com/) 求Rosenbrock函式的最小值
## 2. Python
Python 裡面的 scipy.optimize 提供了豐富的優化演算法,對於 Rosenbrock函式,它的求解程式碼如下:
``` PY
import numpy as np
from scipy.optimize import minimize
def rosenbrock(x):
return (1 - x[0])**2 + 100 * ((x[1] - x[0] * x[0])**2)
x0 = np.array([1.2, 1.2])
best = minimize(rosenbrock, x0)
print(best)
```
`minimize` 有兩個引數,其中 `rosenbrock` 是要去求得最小值得 objective function;`x0` 是初始值,有時候初始值對結果影響很大。
上面程式碼得輸出如下:
```
fun: 3.3496916936926394e-12
hess_inv: array([[0.49944334, 0.99865554],
[0.99865554, 2.00167338]])
jac: array([-4.95083209e-05, 2.79682766e-05])
message: 'Desired error not necessarily achieved due to precision loss.'
nfev: 159
nit: 10
njev: 49
status: 2
success: False
x: array([0.99999874, 0.9999976 ])
```
即 x(1) 和 y(1) 在接近 `(1,1)` 的情況下,Rosenbrock 函式有最小值,最小值接近 0。
也可以通過引數 'method='nelder-mead'