Q-Q圖原理詳解及Python實現
阿新 • • 發佈:2021-01-23
【導讀】在之前的《資料探勘概念與技術 第2章》的文章中我們介紹了Q-Q圖的概念,並且通過呼叫現成的python函式, 畫出了Q-Q圖, 驗證了Q-Q圖的兩個主要作用,1. 檢驗一列資料是否符合正態分佈 2. 檢驗兩列資料是否符合同一分佈。本篇文章將更加全面的為大家介紹QQ圖的原理以及自己手寫函式實現畫圖過程
本文的程式碼檔案(jupyter)和資料檔案可以在我們的公眾號"資料臭皮匠" 中回覆"QQ圖"獲取


 可以看到, 學生的三科總分與標準正態分佈的數值畫出的散點圖, 基本分佈在一條直線附近, 可以認為學生分數符合正態分佈, 但不是標準正態分佈,詳細分析我們在下文會講到。
接下來,我們通過手動畫Q-Q圖 來實現檢驗資料是否符合正態分佈
當兩列資料行數相同時,直接將分別排序後的兩列數值畫散點圖
可以看到, 學生的三科總分與標準正態分佈的數值畫出的散點圖, 基本分佈在一條直線附近, 可以認為學生分數符合正態分佈, 但不是標準正態分佈,詳細分析我們在下文會講到。
接下來,我們通過手動畫Q-Q圖 來實現檢驗資料是否符合正態分佈
當兩列資料行數相同時,直接將分別排序後的兩列數值畫散點圖
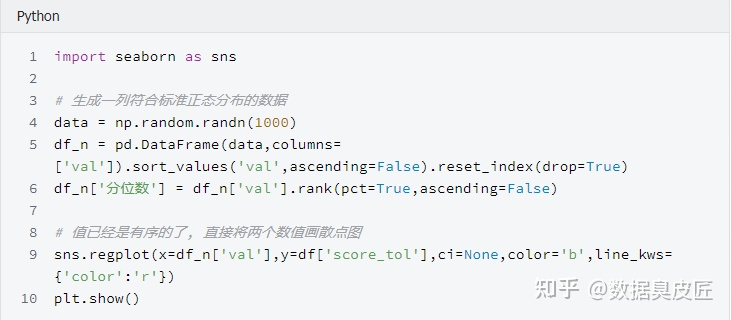
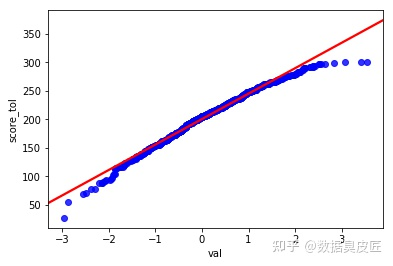 可以看到, 我們畫出了和統計包幾乎一樣的QQ圖(最左側和最右側之間的差異, 是由於正態分佈變數是隨機產生的, 每次都會有一些不同)
直接將分別排序後的兩列數值畫散點圖, 好像不能體現Q-Q圖的本質, 我們接下來取0到100的500個分位數,畫圖看下情況
可以看到, 我們畫出了和統計包幾乎一樣的QQ圖(最左側和最右側之間的差異, 是由於正態分佈變數是隨機產生的, 每次都會有一些不同)
直接將分別排序後的兩列數值畫散點圖, 好像不能體現Q-Q圖的本質, 我們接下來取0到100的500個分位數,畫圖看下情況

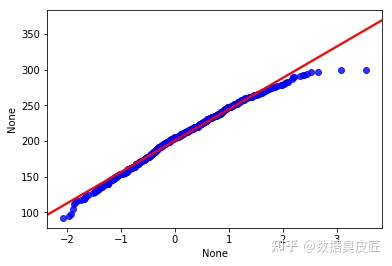 我們畫出了和上面幾乎一樣的圖, 但是可以看到, 右側的點分佈在在直線下方, 結果是符合直覺的, 因為正態分佈的資料在最右側需要有一些比較大的數字, 但是學生成績被總分300 限制住了, 這就印證了一句話,學霸只能考100是因為滿分只有100
檢驗兩列資料是否符合同一分佈
兩列資料行數相同時
我們畫出了和上面幾乎一樣的圖, 但是可以看到, 右側的點分佈在在直線下方, 結果是符合直覺的, 因為正態分佈的資料在最右側需要有一些比較大的數字, 但是學生成績被總分300 限制住了, 這就印證了一句話,學霸只能考100是因為滿分只有100
檢驗兩列資料是否符合同一分佈
兩列資料行數相同時
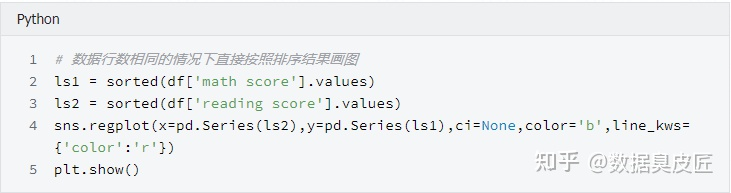
 兩列資料行數不同時
兩列資料行數不同時
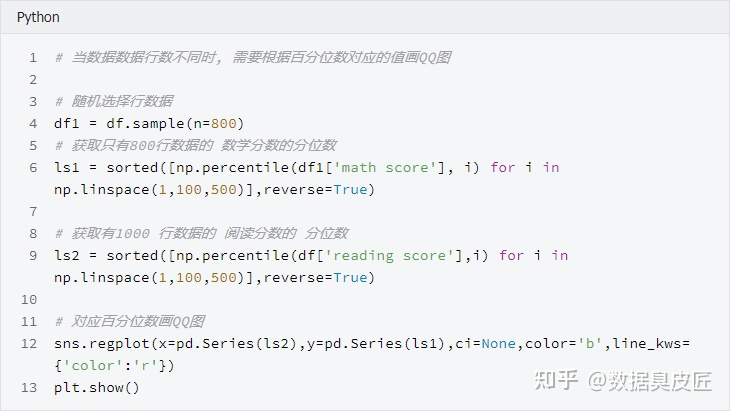
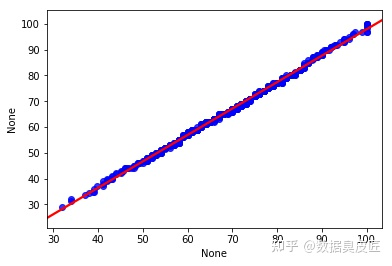 可以看到, 'math score' 和 'reading score' 兩列的分位數分佈在y=x 直線附近, 我們可以認為兩列資料符合同一分佈。
符合正態和標準正態分佈的區別
在上面檢驗資料是否符合正態分佈時,我們說, 學生分數符合正態分佈, 但不是標準正態分佈。是因為通過仔細觀察會發現, 散點圖並不是沿著y=x 線分佈, 而是沿著 y=ax+b 分佈, 即, 一條有截距且有斜率的直線。
Q-Q散點圖是沿著y=x分佈時, 符合標準正態分佈
可以看到, 'math score' 和 'reading score' 兩列的分位數分佈在y=x 直線附近, 我們可以認為兩列資料符合同一分佈。
符合正態和標準正態分佈的區別
在上面檢驗資料是否符合正態分佈時,我們說, 學生分數符合正態分佈, 但不是標準正態分佈。是因為通過仔細觀察會發現, 散點圖並不是沿著y=x 線分佈, 而是沿著 y=ax+b 分佈, 即, 一條有截距且有斜率的直線。
Q-Q散點圖是沿著y=x分佈時, 符合標準正態分佈
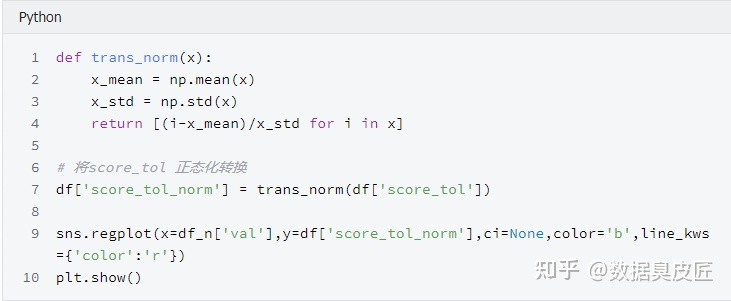
 Q-Q散點圖沿y=ax+b分佈時, 符合正態分佈, 但非標準正態分佈
Q-Q散點圖沿y=ax+b分佈時, 符合正態分佈, 但非標準正態分佈
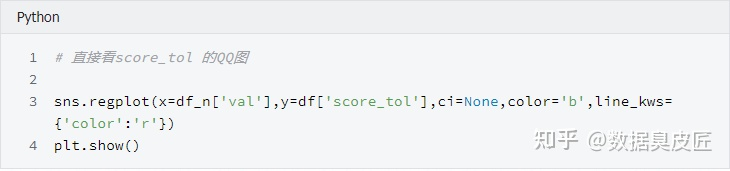
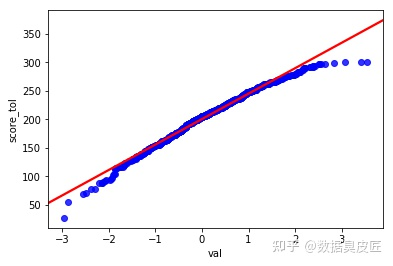 可以看到, 散點圖基本在y = ax+b 的附近分佈, 這時我們可以說,score_tol 列符合正態分佈, 但不是標準正太分佈。
一般認為,Q-Q圖的散點需要分佈在y=x 直線附近才認為符合正態分佈, 為什麼散點圖分佈在y=ax+b附近, 仍然可以認為, score_tol 符合正態分佈呢? 因為, 從圖中可以看到, score_tol 列可以寫成正態分佈的列val 的線性函式 score_tol = a * val + b 而正態分佈的性質決定了, 如果一個變數x服從正態分佈, 那麼他的函式ax+b 也符合正態分佈。
本文的Python程式碼和資料檔案可以在我們的公眾號"資料臭皮匠" 中回覆"QQ圖"獲
取
關注公眾號:資料臭皮匠;獲得更多精彩內容
可以看到, 散點圖基本在y = ax+b 的附近分佈, 這時我們可以說,score_tol 列符合正態分佈, 但不是標準正太分佈。
一般認為,Q-Q圖的散點需要分佈在y=x 直線附近才認為符合正態分佈, 為什麼散點圖分佈在y=ax+b附近, 仍然可以認為, score_tol 符合正態分佈呢? 因為, 從圖中可以看到, score_tol 列可以寫成正態分佈的列val 的線性函式 score_tol = a * val + b 而正態分佈的性質決定了, 如果一個變數x服從正態分佈, 那麼他的函式ax+b 也符合正態分佈。
本文的Python程式碼和資料檔案可以在我們的公眾號"資料臭皮匠" 中回覆"QQ圖"獲
取
關注公眾號:資料臭皮匠;獲得更多精彩內容
Q-Q圖是什麼
QQ圖是quantile-quantile(分位數-分位數圖) 的簡稱,上面也有介紹它的兩個主要作用: 1.檢驗一列資料是否符合正態分佈 2.檢驗兩列資料是否符合同一分佈 Q-Q圖的原理 要弄清Q-Q圖的原理,我們先來介紹下分位數的概念。這裡我們引用下百度百科的介紹: 分位數, 指的就是連續分佈函式中的一個點,這個點對應概率p。若概率0<p<1,隨機變數X或它的概率分佈的分位數Za,是指滿足條件p(X≤Za)=α的實數。 What...?? 是不是感覺有點抽象,彆著急,我們繼續往下看分位數的例項-百分位數。 百分位數

 可以看到, 學生的三科總分與標準正態分佈的數值畫出的散點圖, 基本分佈在一條直線附近, 可以認為學生分數符合正態分佈, 但不是標準正態分佈,詳細分析我們在下文會講到。
接下來,我們通過手動畫Q-Q圖 來實現檢驗資料是否符合正態分佈
當兩列資料行數相同時,直接將分別排序後的兩列數值畫散點圖
可以看到, 學生的三科總分與標準正態分佈的數值畫出的散點圖, 基本分佈在一條直線附近, 可以認為學生分數符合正態分佈, 但不是標準正態分佈,詳細分析我們在下文會講到。
接下來,我們通過手動畫Q-Q圖 來實現檢驗資料是否符合正態分佈
當兩列資料行數相同時,直接將分別排序後的兩列數值畫散點圖

 可以看到, 我們畫出了和統計包幾乎一樣的QQ圖(最左側和最右側之間的差異, 是由於正態分佈變數是隨機產生的, 每次都會有一些不同)
直接將分別排序後的兩列數值畫散點圖, 好像不能體現Q-Q圖的本質, 我們接下來取0到100的500個分位數,畫圖看下情況
可以看到, 我們畫出了和統計包幾乎一樣的QQ圖(最左側和最右側之間的差異, 是由於正態分佈變數是隨機產生的, 每次都會有一些不同)
直接將分別排序後的兩列數值畫散點圖, 好像不能體現Q-Q圖的本質, 我們接下來取0到100的500個分位數,畫圖看下情況

 我們畫出了和上面幾乎一樣的圖, 但是可以看到, 右側的點分佈在在直線下方, 結果是符合直覺的, 因為正態分佈的資料在最右側需要有一些比較大的數字, 但是學生成績被總分300 限制住了, 這就印證了一句話,學霸只能考100是因為滿分只有100
檢驗兩列資料是否符合同一分佈
兩列資料行數相同時
我們畫出了和上面幾乎一樣的圖, 但是可以看到, 右側的點分佈在在直線下方, 結果是符合直覺的, 因為正態分佈的資料在最右側需要有一些比較大的數字, 但是學生成績被總分300 限制住了, 這就印證了一句話,學霸只能考100是因為滿分只有100
檢驗兩列資料是否符合同一分佈
兩列資料行數相同時

 兩列資料行數不同時
兩列資料行數不同時

 可以看到, 'math score' 和 'reading score' 兩列的分位數分佈在y=x 直線附近, 我們可以認為兩列資料符合同一分佈。
符合正態和標準正態分佈的區別
在上面檢驗資料是否符合正態分佈時,我們說, 學生分數符合正態分佈, 但不是標準正態分佈。是因為通過仔細觀察會發現, 散點圖並不是沿著y=x 線分佈, 而是沿著 y=ax+b 分佈, 即, 一條有截距且有斜率的直線。
Q-Q散點圖是沿著y=x分佈時, 符合標準正態分佈
可以看到, 'math score' 和 'reading score' 兩列的分位數分佈在y=x 直線附近, 我們可以認為兩列資料符合同一分佈。
符合正態和標準正態分佈的區別
在上面檢驗資料是否符合正態分佈時,我們說, 學生分數符合正態分佈, 但不是標準正態分佈。是因為通過仔細觀察會發現, 散點圖並不是沿著y=x 線分佈, 而是沿著 y=ax+b 分佈, 即, 一條有截距且有斜率的直線。
Q-Q散點圖是沿著y=x分佈時, 符合標準正態分佈

 Q-Q散點圖沿y=ax+b分佈時, 符合正態分佈, 但非標準正態分佈
Q-Q散點圖沿y=ax+b分佈時, 符合正態分佈, 但非標準正態分佈

 可以看到, 散點圖基本在y = ax+b 的附近分佈, 這時我們可以說,score_tol 列符合正態分佈, 但不是標準正太分佈。
一般認為,Q-Q圖的散點需要分佈在y=x 直線附近才認為符合正態分佈, 為什麼散點圖分佈在y=ax+b附近, 仍然可以認為, score_tol 符合正態分佈呢? 因為, 從圖中可以看到, score_tol 列可以寫成正態分佈的列val 的線性函式 score_tol = a * val + b 而正態分佈的性質決定了, 如果一個變數x服從正態分佈, 那麼他的函式ax+b 也符合正態分佈。
本文的Python程式碼和資料檔案可以在我們的公眾號"資料臭皮匠" 中回覆"QQ圖"獲
取
關注公眾號:資料臭皮匠;獲得更多精彩內容
可以看到, 散點圖基本在y = ax+b 的附近分佈, 這時我們可以說,score_tol 列符合正態分佈, 但不是標準正太分佈。
一般認為,Q-Q圖的散點需要分佈在y=x 直線附近才認為符合正態分佈, 為什麼散點圖分佈在y=ax+b附近, 仍然可以認為, score_tol 符合正態分佈呢? 因為, 從圖中可以看到, score_tol 列可以寫成正態分佈的列val 的線性函式 score_tol = a * val + b 而正態分佈的性質決定了, 如果一個變數x服從正態分佈, 那麼他的函式ax+b 也符合正態分佈。
本文的Python程式碼和資料檔案可以在我們的公眾號"資料臭皮匠" 中回覆"QQ圖"獲
取
關注公眾號:資料臭皮匠;獲得更多精彩內容
作者:範小匠
稽核:灰灰匠
編輯:森匠
