在資料分析統計的場景裡，常用的方法除了描述性統計方法外，還有推斷統計方法，如果再從工作性質上來劃分，推斷統計包含了引數估計和假設驗證這兩方面的內容。而推斷統計用到了很多概率統計方法，所以本小節在介紹推斷統計的內容前，還將講述一些常用的概率統計方法。

1 分析收盤價，繪製小提琴圖

    小提琴圖綜合了箱狀圖與核密度圖的特性，從箱狀圖裡能看出資料的各分位數，而從核密度圖裡，能看出樣本資料的分佈情況，即每個數值點上樣本的密度。

    從統計學的角度來分析，樣本密度越大的數值區域，接下來的資料出現在這裡的概率也就越大。在如下的ViolinplotDemo.py範例中，將通過matplotlib庫的violinplot方法，繪製基於股票收盤價的小提琴圖，同時也將對比性地繪製出箱狀圖，從中大家能直觀地理解“核密度”的概念。    

1	import pandas as pd
2	import matplotlib.pyplot as plt
3	filename='D:\\work\\data\\ch9\\6007852019-06-012020-01-31.csv'
4	df = pd.read_csv(filename,encoding='gbk',index_col=0)
5	fig = plt.figure()
6	plt.rcParams['font.sans-serif']=['SimHei']
7	axViolin = fig.add_subplot(121)
8	axViolin.violinplot(df['Close'],showmeans=True,showmedians=True)
9	axViolin.set_title('描述收盤價的小提琴圖')
10	axViolin.grid(True) 	# 帶網格線
11	axBoxplot = fig.add_subplot(122)
12	axBoxplot.boxplot(df['Close'])
13	axBoxplot.set_title('描述收盤價的箱狀圖')
14	axBoxplot.grid(True) 	# 帶網格線
15	plt.show()
 

    在第4行裡，從之前範例準備好的csv檔案裡得到了股票資料。在第7行和第11行裡，通過add_subplot方法，繪製了兩個子圖。

    在第一個子圖裡，通過violinplot方法，根據第一個引數df[‘Close’]，繪製了基於股票收盤價的小提琴圖，其中showmeans引數表示是否要繪製資料平均線，而showmedians引數則表示是否要繪製資料的中位線，即第50的百分位數。而在第二個子圖裡，則通過第12行的boxplot方法，繪製基於收盤價的箱狀圖，上述程式碼的執行效果如下圖所示。

​

    對比左右兩個子圖，能發現兩者的中位線是一致的，而且左邊小提琴圖裡，在約15.4的位置還有一條樣本資料平均線的圖。此外，小提琴圖裡，能看到從上往下藍色區域寬窄不一，寬的區域表示其中樣本分佈較多，窄的區域則相反，從中能直觀地看到收盤價資料的分佈情況。

2 用直方圖來擬合正態分佈效果

    正態分佈是一種連續隨機變數概率分佈，它是很多分析統計方法的基礎，比如包括迴歸分析等在內的多種方法均要求被分析的樣本服從正態分佈。

    正態分佈和直方圖相似點在於，它們都能展示變數的分佈情況，所以在如下的DrawNormal.py範例中，將先用直方圖來擬合正態分佈的效果，從中大家能直觀地感受到正態分佈，隨後會再此基礎上做進一步分析。    

1	# coding=utf-8
2	import numpy as np
3	import matplotlib.pyplot as plt
4	fig = plt.figure()
5	ax = fig.add_subplot(111)
6	u = 0
7	sigma = 1
8	num = 1000000
9	points = np.random.normal(u, sigma, num)
10	#以直方圖來擬合正態分佈
11	ax.hist(points, bins=1000)
12	plt.show()

    正態分佈有兩個關鍵引數，分別是期望μ和方差為σ^2（即σ的平方），在第6行和第7行裡，分別定義這兩個關鍵變數。在第9行裡，通過numpy.random.normal方法，以兩個關鍵引數，生成了1000000個符合正態分佈的隨機數，其中生成的個數有第3個引數num指定。

    在準備好資料後，是通過第11行的hist方法，繪製了描述樣本points分佈情況的直方圖，其中通過bins引數指定了直方圖裡的柱狀圖的個數。

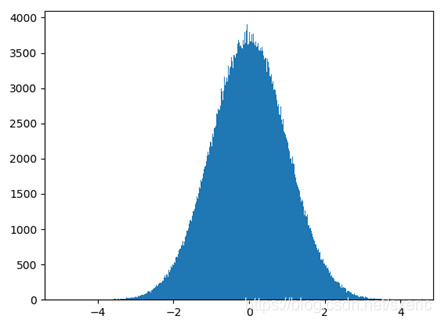
    執行本範例後，能看到如下圖9.9所示的效果。從中能看到滿足正態分佈的隨機樣本具有如下的特性。

• 正態分佈曲線呈鍾狀，是關於數學期望μ對稱，數學期望可以理解成是該隨機樣本數的平均值，而中間的高度是由方差決定的。
• 從圖上能看到這些隨機數的分佈情況，而0位置的分佈最為密集，其中0是生成該正態分佈隨機數時指定的數學期望值。
• 而且，滿足正態分佈的隨機變數樣本集，大約68.3%的樣本落在距數學期望值有1個標準差（即σ）的範圍內，大約95.4%樣本落在在距數學期望值有2個標準差（即2σ）的範圍內，大約99.7%樣本落在距數學期望值有3個標準差（即3σ）內的範圍內。

​

3 驗證序列是否滿足正態分佈

    之前提到，很多數學統計規律和方法是基於正態分佈的，也就是說，如果某組樣本變數符合正態分佈，那麼就可以用到這些規律和方法來進行分析或預測工作。那麼怎麼檢驗序列是否滿足正態分佈呢？在scipy.stats模組裡封裝了normaltest方法，可以用它來檢驗，在如下的CheckNormal.py範例中，演示了通過該方法的用法。    

1	# coding=utf-8
2	import numpy as np
3	from scipy.stats import normaltest
4	import pandas as pd
5	u = 0
6	sigma = 1
7	num = 1000
8	normalArray = np.random.normal(u, sigma, num)
9	#驗證是否是正態分佈
10	print(normaltest(normalArray))
11	filename='D:\\work\\data\\ch9\\6007852020-01-012020-01-31.csv'
12	df = pd.read_csv(filename,encoding='gbk',index_col=0)
13	print(normaltest(df['Close']))

    在第5行到第8裡，指定了期望和方法，生成了1000個隨機數，在第10行裡，通過normaltest方法驗證該序列是否符合正態分佈。由於是生成隨機數，所以每次結果不會相同，如下給出了其中一次的執行結果。

1. NormaltestResult(statistic=1.9905539749433805, pvalue=0.36962104996359296)

    其中主要看pvalue，從統計學上看，這個數有三檔意義，第一檔是大於0.05，表示兩者差別無顯著意義。這裡結果約為0.37，符合這一檔。該取值在當前上下文中的含義是，該序列和正態分佈序列間，差別無顯著意義，即normalArray序列符合正態分佈， 由於待檢驗的該序列本身就是以正態分佈的方式生成的，所以這個結論無疑是正確的。

    隨後在第11行和第12行裡，從csv檔案裡得到股票資料，並用第13行的normaltest方法驗證收盤價是否滿足正態分佈，這行print語句的執行結果如下。

1. NormaltestResult(statistic=4.624089377177887, pvalue=0.09905850056321942)

    雖然pvalue的值0.099比0.05大不了多少，但也能說明股票收盤價的序列滿足正態分佈。

4 引數估計方法

    引數估計方法是推斷統計的一種方法，該方法的理論基礎是正態分佈，也就是說，如果該方法的適用範圍是滿足正態分佈的序列。引數估計可以再劃分成點估計和區間估計，其中點估計的含義是用樣本的引數來估計總量中的引數。

    點估計的一個應用場景是抽樣檢驗，其中可以用樣本產品的“產品最大工作時間”引數來估計所有產品中的該數值。而區間估計要解決的問題是，根據事先制定的正確度與精確度引數，構造適當的區間範圍。通俗地講，通過區間估計能確定“有多少把握能確保某個樣本在某個區間範圍內”。

    從上例中已經看到，收盤價是符合正態分佈，而且它適用於“區間估計”的場景。在如下的IntervalEst.py範例中，將呼叫scipy.stats裡的interval方法，以95%的置信度，給出該股收盤價的置信區間。   

1	# coding=utf-8
2	from scipy import stats
3	import pandas as pd
4	filename='D:\\work\\data\\ch9\\6007852020-01-012020-01-31.csv'
5	df = pd.read_csv(filename,encoding='gbk',index_col=0)
6	print(stats.t.interval(0.95,len(df['Close'])-1,df['Close'].mean(),df['Close'].std()))

    在前5行裡，從csv檔案裡得到了指定股票在指定範圍內的資料，在第6行裡，通過呼叫了stats.t.terval方法，計算了df[‘Close’]的置信區間。

    其中第1個引數表示置信度，第2個引數表示自由度，一般是樣本數減1，第3個引數一般傳入的是均值，第4個引數則表示標準差的計算方式。執行上述範例，能看到如下的輸出結果。

1. (14.576210752919142, 16.423789119924283)

    這表示在95%置信度的前提下，該序列的區間範圍。

5 顯著性驗證

    顯著性驗證是假設驗證中的一種。假設驗證的思想是，先對樣本資料做個假設，然後驗證該假設對不對。

    再具體一下，如果原假設是對的，而驗證的結果卻告訴你要放棄該假設，這叫第一類錯誤，在假設驗證裡把第一類錯誤出現的概率記成α。但如果原假設不對，而結果卻要你接收該假設，這叫第二類錯誤，記作β。

    一般只考慮出現第一類錯誤的最大概率α，而不考慮出現第二類錯誤的概率β，這樣的假設檢驗就叫顯著性檢驗，其中出錯概率α叫顯著性水平。在顯著性驗證裡，α一般的取值有0.05、0.025和0.01這三種，對應地表示出現第一類錯誤的可能性必須低於5%、2.5%或1%。

    根據樣本的概率分佈情況，常用的校驗方法有t檢驗、z檢驗和F檢驗等，其中通過t檢驗可以檢驗服從正態分佈的標準差未知的樣本序列的均值。在如下的TTestDemo.py範例中，就將演示用t檢驗驗證收盤價的均值。    

1	# coding=utf-8
2	from scipy import stats
3	import pandas as pd
4	filename='D:\\work\\data\\ch9\\6007852020-01-012020-01-31.csv'
5	df = pd.read_csv(filename,encoding='gbk',index_col=0)
6	print(df['Close'].mean()) #15.499999936421712
7	print(stats.ttest_1samp(df['Close'],15.5))
8	print(stats.ttest_1samp(df['Close'],15.4))
9	print(stats.ttest_1samp(df['Close'],15.7))
10	print(stats.ttest_1samp(df['Close'],15.2))
11	print(stats.ttest_1samp(df['Close'],16))

    在第6行裡，輸出了股票收盤價的均值，約為15.5，在第7行到第11行裡，提出了不同的關於收盤價均值的假設，並通過stats模組裡的ttest_lsamp方法，對不同的假設進行了t檢驗。上述範例執行後的結果如下所示。    

1	15.499999936421712
2	Ttest_1sampResult(statistic=-5.716967037005381e-07, pvalue=0.9999995519184666)
3	Ttest_1sampResult(statistic=0.8992005958223217, pvalue=0.38375142019051156)
4	Ttest_1sampResult(statistic=-1.7984029067347544, pvalue=0.09370333462557079)
5	Ttest_1sampResult(statistic=2.6976029308603886, pvalue=0.017337840975255838)
6	Ttest_1sampResult(statistic=-4.496006409291847, pvalue=0.0005030226952314426)

     上述輸出結果的第1行表示序列的均值，從第2行到第6行的pvalue結果裡，能看到對不同假設的驗證結果，詳細說明請參考下表裡的內容。

    也就是說，如果待驗證的均值越接近於真實的均值，那麼pvalue的取值就越高，說明“該數值是正確均值”的假設成立的可能性就越高，反之pvalue取值就很低，比如針對“均值是16”的假設，成立的概率才約0.0005，就說明該假設基本不成立。

本文出自我寫的書： Python爬蟲、資料分析與視覺化：工具詳解與案例實戰，https://item.jd.com/10023983398756.html

     ​

    請大家關注我的公眾號：一起進步，一起掙錢，在本公眾號裡，會有很多精彩文章。