樹秀於林風必摧之——線段樹
阿新 • • 發佈:2017-05-11
線段 strong pda -1 自己的 我們 不重復 ebe wid
關於線段樹,其實我一開始也是很懵的,但看久了也就習慣了。
以下是我對線段樹的一點理解,寫得不好,也請各位看官見諒。
搜狗定義:線段樹(Segment Tree)是一種二叉搜索樹,它將一個區間劃分成一些單元區間,每個單元區間對應線段樹中的一個葉結點。
定義還是很顯然的。
那麽線段樹都能做些什麽呢?
在n個數中有m個詢問,詢問如下:
1.把q這個數改成v O(logn);
2.求在1~n這個區間的和.
接下來我們講原理(當然原理也是我自己的理解,可能不是正解,但我想,線段樹這個東西大概就是這樣的吧)
首先看圖
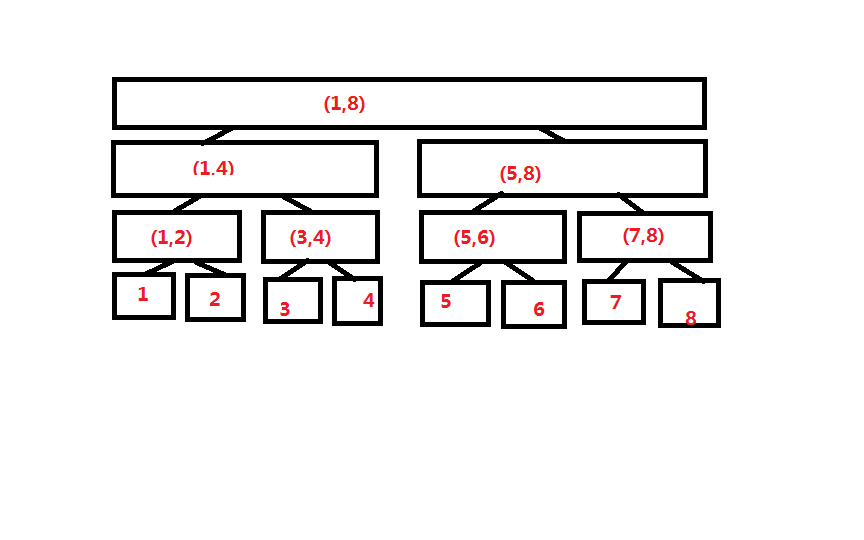
下面我們將原理
1.它是用“二進制”存儲的
什麽是“二進制”存儲?
眾所周知,用二的倍數可以表示所有的數
例:13=1+4+8;
(具體原理請參考二進制和十進制的轉換)
那麽線段樹也是這樣:
如:我們要查找(2,5)這個區間,那它就是2+(3,4)+5所代表的數(區間和)
2.它是“二分查找”(當然不是嚴格意義上的)
二分查找不再贅述
例:當我們要把6這個位置上所在的數改為★,那我們一定是這樣查找的:
(1,8)->(5,8)->(5,6)->(6)->(★)
那麽怎麽實現呢?我大概總結了一下幾個步驟:
1.建立線段樹
2.查找位置+動作
具體代碼如下
int a[maxn];//每個數的值 int sum[maxn*4];//區間和 void update(int rt) { sum[rt]=sum[rt*2]+sum[rt*2+1];//前綴和思想 } void build(int l,int r,int rt)//建立樹,左孩子,右孩子,根 { if(l==r) { sum[rt]=a[l]; return ;//邊界 } int m=(l+r)/2; build(1,m,rt*2); build(m+1,r,rt*2+1); update(rt);//合並兩個兒子 }
//如果不理解左孩子右孩子為什麽要那樣寫的,看這裏:
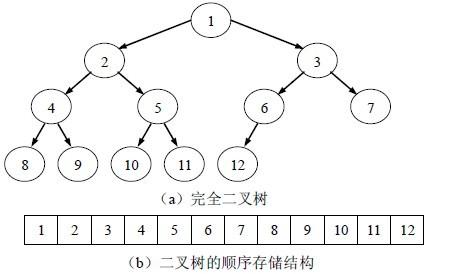
以根節點為例:(1)
左孩子:1*2=2;
右孩子:1*2+1=3;
這樣就能保證樹在數組裏存滿且不重復。
void modify(int l,int r,int rt,int p,int v)//將p的位置上的數改為v { if(l==r) { sum[rt]=v; return ;//找到這個數了,改值。當然我們也會順便把與它相關的所有值都改掉 } int m=(l+r)/2; if(p<=m) modify(1,m,rt*2,p,v); else modify(m+1,r,rt*2+1,p,v);//二分查找 update(rt); } int query(int l.int r,int rt,int nowl,int nowr)//詢問(nowl,nowr)這個區間和 { if(nowl<=1&&r<=nowr)//邊界 return sum[rt]; int m=(l+r)/2; int ans=0; if(nowl<=m)ans+=query(1,m,rt*2,nowl,nowr); if(m<nowr)ans+=query(m+1,r,rt*2+1,nowl,nowr);//查找求和 return ans; }
這是兩次詢問。
主函數的話就依據情況調用這三個函數就好了
那我要講的,大概就是這些了。
byebey!^_^
樹秀於林風必摧之——線段樹
