圖 續2
-----------------siwuxie095
圖的遍歷
圖的遍歷 分為:深度優先搜索 和 廣度優先搜索
不同的方式在遍歷時,遍歷路徑是不一樣的
深度優先搜索
對如下圖進行深度優先搜索:
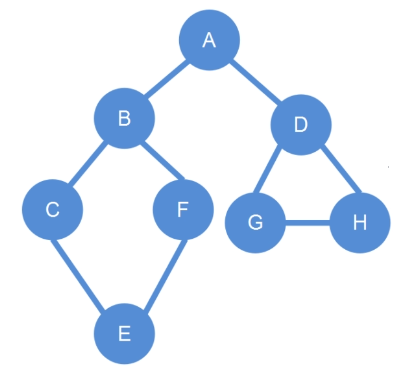
需要先選定一個點,假設選定的點為 A
先從 A 的一支開始搜索,搜索到 B,接著:
從 B 搜索到 C,從 C 搜索到 E,從 E 搜索到 F,直到
從 F 再搜索時已經形成了一個環為止
再從 A 的另一支開始搜索,搜索到 D,接著:
從 D 搜索到 G,從 G 搜索到 H,直到從 H 再搜索時
已經形成了一個環為止
通過上面的搜索過程,不難發現,這與二叉樹的前序遍歷的
根 - 左 - 右 模式 非常相似
其實,對於圖的深度優先搜索來說, 就是前序遍歷:
先搜索根,然後再搜索與根連接的每一個節點,而且需要深入
到這個節點的最終端
最後:
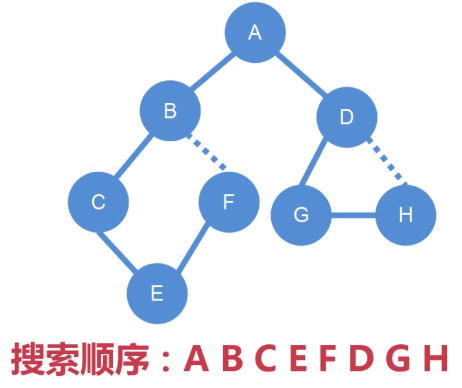
深度優先搜索的順序:A B C E F D G H
其中:B 到 F 的邊,和 D 到 H 的邊,需要舍棄掉,
因為它們已經使得當前的這棵樹形成了一個環
廣度優先搜索
廣度優先搜索 其實比 深度優先搜索 更容易理解
對如下圖進行廣度優先搜索:
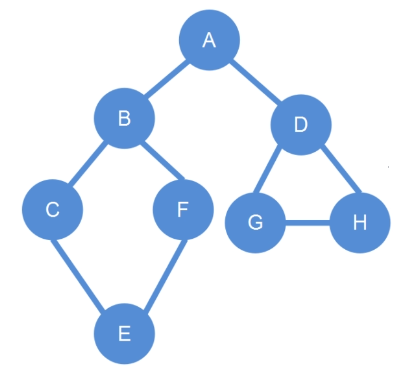
如果把這張圖分成層,廣度優先搜索其實就是一層一層的去搜索,
它的搜索順序就是先搜索 A,再搜索 B、D,然後搜索 C、F、G、
H,最後搜索 E
最後:
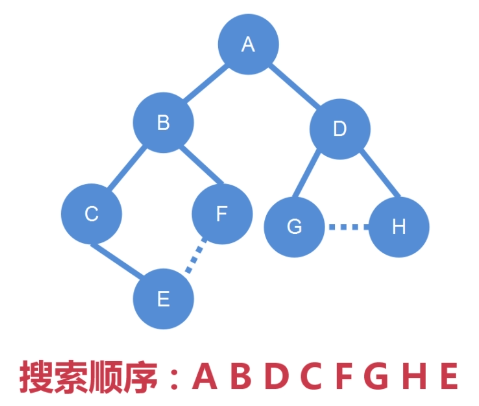
廣度優先搜索的順序:A B D C F G H E
其中:E 到 F 的邊,和 G 到 H 的邊,需要舍棄掉,
因為它們已經使得當前的這棵樹形成了一個環
最小生成樹
通過對 深度優先搜索 和 廣度優先搜索 的了解,不難發現,
采用不同的搜索方式,形成的生成樹是不一樣的
但是這樣的遍歷,其實還是相對比較簡單的,它並沒有涉及
到權值的問題。在一張圖中,頂點和頂點之間的邊如果是有
權值的,它的問題將會更加復雜
這樣,就涉及到 最小生成樹 的問題
看如下實例:
有這樣六個城市,分別叫 A、B、C、D、E、F,需要在六個城市
之間修路(可以看成是六個頂點)
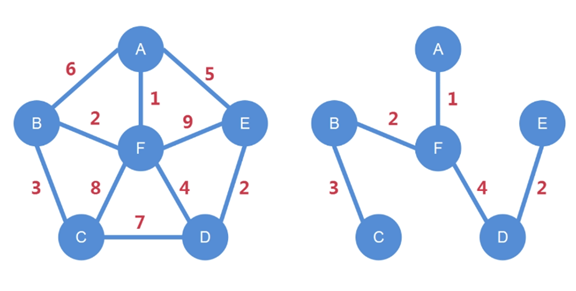
其實每兩個城市之間都可以修路,但是修路的成本可能不一樣,中間也許隔著山
如:從 A 市修向 B 市,如果中間隔著山,成本就會很高,假設權值為 6
那就不如先從 A 市修到 F 市,再從 F 市修到 B 市,這樣,總權值才為 3
可見:如果有了權值之後,想把所有頂點全部連接起來,且使得最後連接
起來的結果最為經濟,這樣,就是一顆最小生成樹
希望達到的結果是這樣:
從 A 開始:A 修到 F,F 修到 B,B 修到 C,F 修到 D,D 修到 E
不難發現,選擇的全是值比較小的邊,而加起來的總成本也最小
但是,有了左圖,通過它去求一棵最小生成樹,從而達到右圖的
效果,卻是需要一套算法的
這樣的算法,共有兩種:

一種叫做 普裏姆(Prim)算法,一種叫做 克魯斯卡爾(Kruskal)算法
普裏姆(Prim)算法
普裏姆(Prim)算法的基本思想:
1)首先要有一個點集合,是指納入到最小生成樹中的點集合
2)其次要有一個邊集合,是指納入到最小生成樹中的邊集合
3)最後要有一個待選邊集合,是指被選定點可以到達的所有邊的集合
第一步:
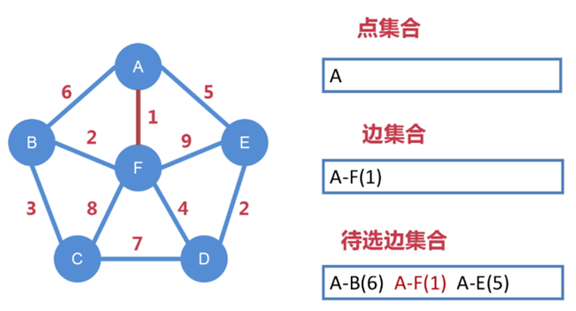
假設從 A 點開始,則 A 就是選定的第一個點,把 A 納入到點集合中
從 A 向外延伸出去一共有三條邊,分別是 A-B、A-F、A-E,把這三
條邊納入到待選邊集合中
從待選邊集合中找出權值最小的邊,即 A-F,把 A-F 納入到邊集合中
這樣,第一個點 和 第一條邊 就確定下來了
第二步:
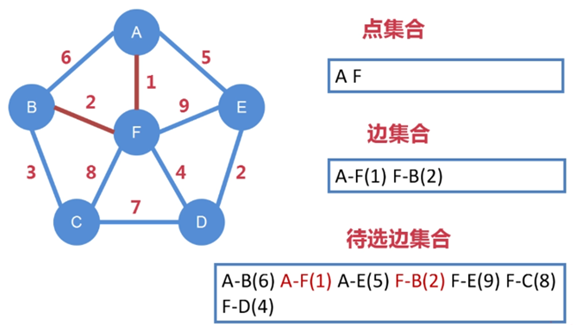
邊 A-F 連接了下一個點 F,把 F 納入到點集合中
把從 A、F 向外延伸出的所有邊都納入到待選邊集合中
待選邊集合進一步擴充,變成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D
「註意:同一條邊,不需要重復寫,如:A-F 和 F-A」
其中 A-F 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 F-B,把 F-B 納入到邊集合中
第三步:
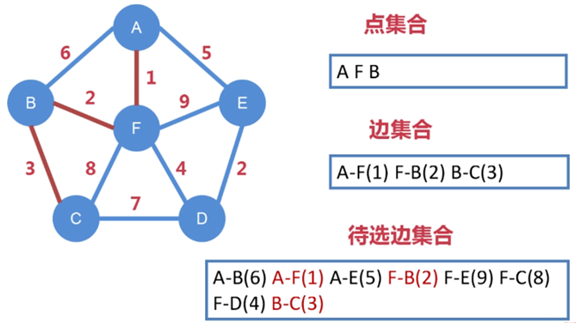
邊 F-B 連接了下一個點 B,把 B 納入到點集合中
把從 A、F、B 向外延伸出的所有邊都納入到待選邊集合中
待選邊集合進一步擴充,變成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D、B-C
其中 A-F、F-B 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 B-C,把 B-C 納入到邊集合中
第四步:
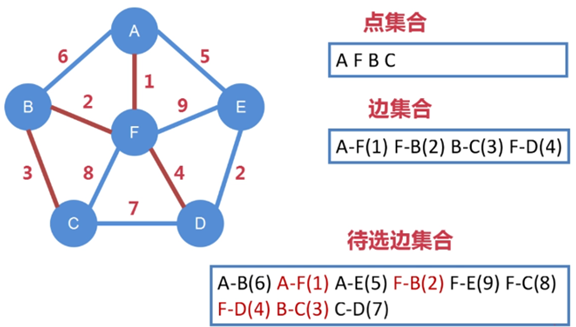
邊 B-C 連接了下一個點 C,把 C 納入到點集合中
把從 A、F、B、C 向外延伸出的所有邊都納入到待選邊集合中
待選邊集合進一步擴充,變成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D、B-C、C-D
其中 A-F、F-B、B-C 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 F-D,把 F-D 納入到邊集合中
第五步:
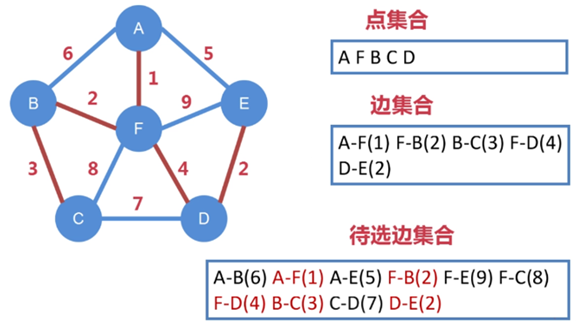
邊 F-D 連接了下一個點 D,把 D 納入到點集合中
把從 A、F、B、C、D 向外延伸出的所有邊都納入到待選邊集合中
待選邊集合進一步擴充,變成 A-B、A-F、A-E、F-B、F-E、
F-C、F-D、B-C、C-D、D-E
其中 A-F、F-B、B-C、F-D 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 D-E,把 D-E 納入到邊集合中
第六步:
邊 D-E 連接了下一個點 E,把 E 納入到點集合中
此時,點集合中有 A、F、B、C、D、E,即 全部六個點都被連接
了起來,形成了一棵最小生成樹
克魯斯卡爾(Kruskal)算法
克魯斯卡爾(Kruskal)算法的基本思想:
1)首先要有一個待選邊集合,是指一張圖中所涉及的所有邊的集合
1)其次要有一個已選邊集合,是指納入到最小生成樹中的邊集合
2)最後要有一個已涉及點集合,是指納入到最小生成樹中的點集合
第一步:
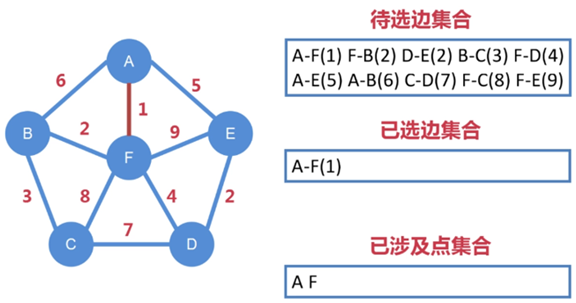
首先把這張圖中所涉及的所有邊都納入到待選邊集合中
從待選邊集合中找出權值最小的邊,即 A-F,把 A-F 納入到已選邊集合中
選定邊的同時,也選定了點,把 A、F 納入到第一個已涉及點集合中
第二步:
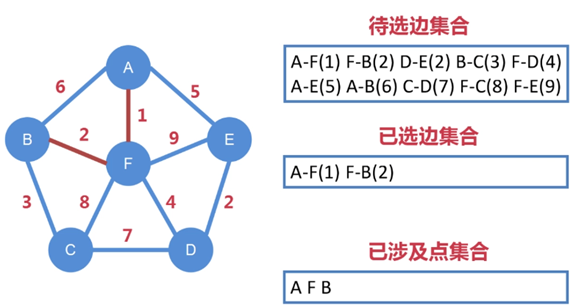
待選邊集合中 A-F 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 F-B,把 F-B 納入到已選邊集合中
選定邊的同時,也選定了點,把 B 納入到第一個已涉及點集合中
其實 D-E 的權值也為 2,F-B 和 D-E 二者任選其一即可,這裏先選 F-B,
F-B 選出來之後、納入到已選邊集合之前,要判斷一下:
當前的 F-B 有沒有與以前的 A-F 形成閉環,如果形成了閉環,就需要將
這條邊拋棄掉
顯然,這裏沒有形成閉環,於是 F-B 這條邊就被納入到已選邊集合中
即 每次從待選邊集合中選邊時,都要做如下操作:
1)當最小權值的邊有多條時,任選其一
2)如果當前選定的邊與已選邊集合中的邊形成了閉環,
就將這條邊拋棄掉,重新選擇
第三步:
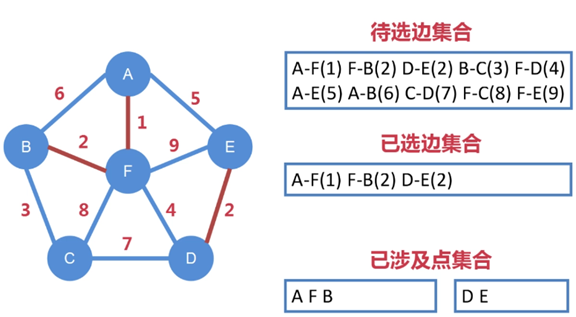
待選邊集合中 A-F、F-B 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 D-E,把 D-E 納入到已選邊集合中
註意:默認在 D-E 納入到已選邊集合之前,就已經判斷沒有形成閉環
選定邊的同時,也選定了點,把 D、E 納入到第二個已涉及點集合中
因為通過已選定邊集合無法讓 A、F、B 和 D、E 相連,所以要納入到
兩個不同的已涉及點集合中
第四步:
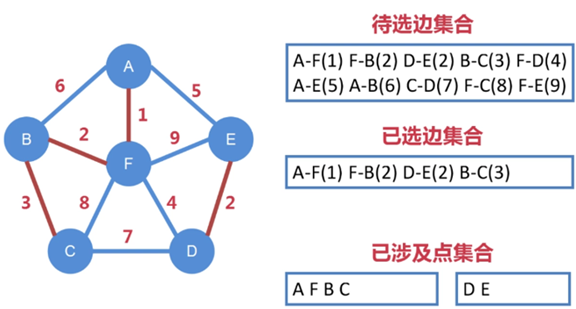
待選邊集合中 A-F、F-B、D-E 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 B-C,把 B-C 納入到已選邊集合中
註意:默認在 B-C 納入到已選邊集合之前,就已經判斷沒有形成閉環
選定邊的同時,也選定了點,把 C 納入到第一個已涉及點集合中
因為通過已選定邊集合無法讓 A、F、B、C 和 D、E 相連,所以要納入到
兩個不同的已涉及點集合中
第五步:

待選邊集合中 A-F、F-B、D-E、B-C 已被選走,不能再被選
從剩下待選邊集合中找出權值最小的邊,即 F-D,把 F-D 納入到已選邊集合中
註意:默認在 F-D 納入到已選邊集合之前,就已經判斷沒有形成閉環
已選定邊集合中的 F-D 使得兩個不同的已涉及點集合中的 F 和 D 關聯了起來,
即 兩個不同的已涉及點集合有了聯系,融合成為一個已涉及點集合
此時,已涉及點集合中有 A、F、B、D、E、C,即 全部六個點都被連接
了起來,形成了一棵最小生成樹
【made by siwuxie095】
圖 續2
