Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

題目大意：給定一個一個m*n格的方針，每個方格都放一個非負數，找到一條從左上角到右下角的路使得經過的格子的數字之和最小。只能往右走或者往下走

解題思路：

構建一個大小為m*n的矩陣，矩陣內每個值為從起點走到該點的最短距離，直到終點。

分為三種情況

1、第一列每個格只能從它的上一個格走下來，所以最左邊一列的數為它上面一個點的值加上原方陣中該點位置上的值

2、第一行每個格只能從它的左邊一個格走過來，所以最上邊一行的數為它左邊一個點的值加上原方陣中該點位置上的值

3、如果不是在第一行或者第一列，則該方格可以從它上面一個格走下來或者從它左邊一個格做過來，因此需要比較上面一格的數值和左邊一格的數值

求出最小值，再加上方陣中該格的數值。

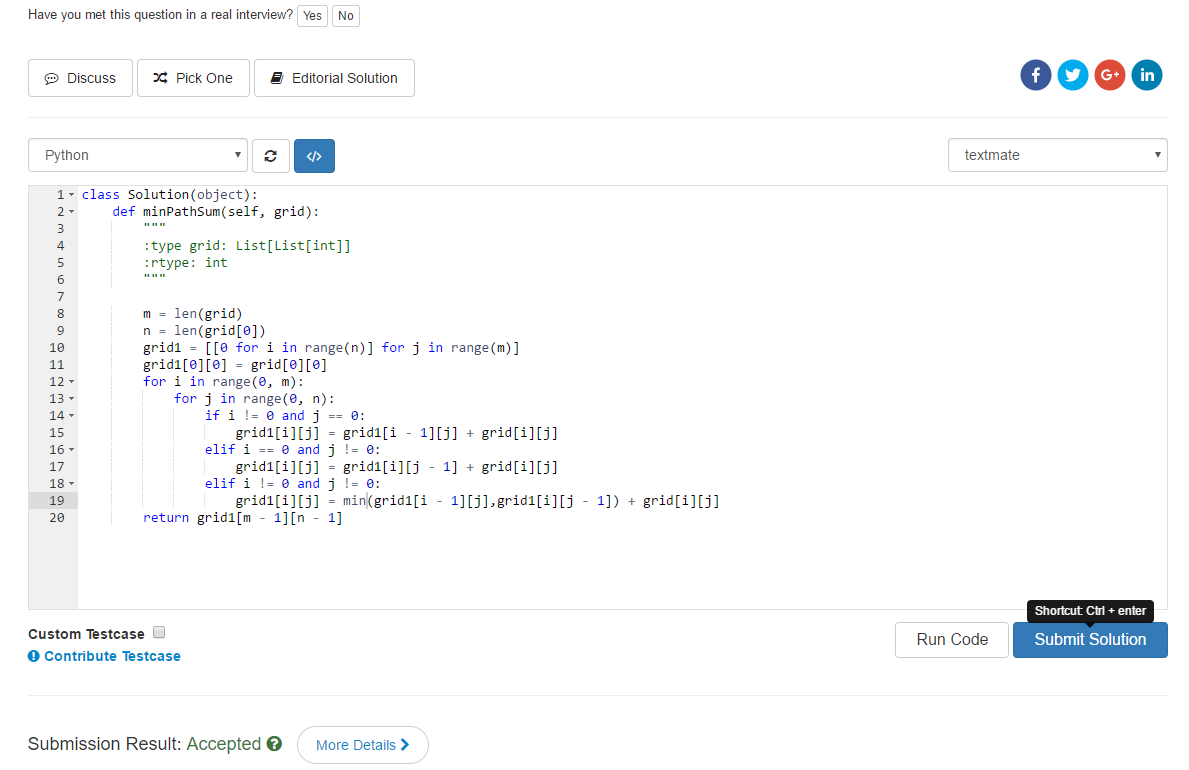
class Solution(object):
　　def minPathSum(self, grid):
　　　　"""
　　　　:type grid: List[List[int]]
　　　　:rtype: int
　　　　"""

　　　　m = len(grid)
　　　　n = len(grid[0])
　　　　grid1 = [[0 for i in range(n)] for j in range(m)]
　　　　grid1[0][0] = grid[0][0]
　　　　for i in range(0, m):
　　　　　　for j in range(0, n):
　　　　　　　　if i != 0 and j == 0:
　　　　　　　　　　grid1[i][j] = grid1[i - 1][j] + grid[i][j]
　　　　　　　　elif i == 0 and j != 0:
　　　　　　　　　　grid1[i][j] = grid1[i][j - 1] + grid[i][j]
　　　　　　　　elif i != 0 and j != 0:
　　　　　　　　　　grid1[i][j] = min(grid1[i - 1][j],grid1[i][j - 1]) + grid[i][j]
　　　　return grid1[m - 1][n - 1]

LeetCode 64. Minimum Path Sum 20170515