【BZOJ4869】相逢是問候 [線段樹]
阿新 • • 發佈:2017-05-23
lib 替換 rip input 次方 一行 event bfc 同時
[Submit][Status][Discuss]
1 2 3 4
0 1 4
0 1 4
1 1 3
3
首先如果b%phi(p),意味著a^b在%p下同余。
如果這一次b%phi(phi(p)),意味著a^b在phi(p)下同余,
同時也意味著下一次在%phi(p)意義下。
我們要讓答案最後是在%p意義下的,那麽顯然每次b%phi[times-1]。
再帶上快速冪,那麽這樣效率就是O(nlog^3(n))的。
相逢是問候
Time Limit: 40 Sec Memory Limit: 512 MB[Submit][Status][Discuss]
Description
Informatikverbindetdichundmich. 信息將你我連結。B君希望以維護一個長度為n的數組,這個數組的下標為從1到n的正整數。一共有m個操作,可以 分為兩種:0 l r表示將第l個到第r個數(al,al+1,...,ar)中的每一個數ai替換為c^ai,即c的ai次方,其中c是 輸入的一個常數,也就是執行賦值ai=c^ai1 l r求第l個到第r個數的和,也就是輸出:sigma(ai),l<=i<=rai因為Input
第一行有三個整數n,m,p,c,所有整數含義見問題描述。 接下來一行n個整數,表示a數組的初始值。 接下來m行,每行三個整數,其中第一個整數表示了操作的類型。 如果是0的話,表示這是一個修改操作,操作的參數為l,r。 如果是1的話,表示這是一個詢問操作,操作的參數為l,r。Output
對於每個詢問操作,輸出一行,包括一個整數表示答案mod p的值。Sample Input
4 4 7 21 2 3 4
0 1 4
0 1 4
1 1 3
Sample Output
03
HINT
1 ≤ n ≤ 50000, 1 ≤ m ≤ 50000, 1 ≤ p ≤ 100000000, 0 < c <p, 0 ≤ ai < pSolution
首先,我們運用歐拉定理: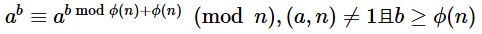
然後還有一個定理:一個數在執行log次操作後,值不會改變。
於是乎,我們可以運用線段樹,暴力修改每一個值,如果值都不變了則不修改。
然後我們再考慮一下,怎麽修改這個值:
已知a(原值)和times(修改次數),我們考慮每一次%什麽,
考慮每一次b的模數。
首先如果b%phi(p),意味著a^b在%p下同余。
如果這一次b%phi(phi(p)),意味著a^b在phi(p)下同余,
同時也意味著下一次在%phi(p)意義下。
我們要讓答案最後是在%p意義下的,那麽顯然每次b%phi[times-1]。
再帶上快速冪,那麽這樣效率就是O(nlog^3(n))的。
Code

#include<iostream>
#include<string>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
using namespace std;
typedef long long s64;
const int ONE = 500005;
const int INF = 2147483640;
int n,m,p,C;
int opt,x,y;
int a[ONE],phi[ONE],p_num;
int MOD;
int res;
struct power
{
int value;
int cnt;
}Node[ONE];
int get()
{
int res=1,Q=1;char c;
while( (c=getchar())<48 || c>57 )
if(c==‘-‘)Q=-1;
res=c-48;
while( (c=getchar())>=48 && c<=57 )
res=res*10+c-48;
return res*Q;
}
int Getphi(int n)
{
int res = n;
for(int i=2; i*i<=n; i++)
if(n % i == 0)
{
res = res/i*(i-1);
while(n % i == 0) n /= i;
}
if(n != 1) res = res/n*(n-1);
return res;
}
int Quickpow(int a,int b,int MOD)
{
int res = 1;
while(b)
{
if(b & 1) res = (s64)res * a % MOD;
a = (s64)a * a % MOD;
b >>= 1;
}
return res;
}
void Build(int i,int l,int r)
{
if(l == r)
{
Node[i].value = a[l] % MOD;
return;
}
int mid = l+r>>1;
Build(i<<1, l, mid);
Build(i<<1|1, mid + 1, r);
Node[i].value = (Node[i<<1].value + Node[i<<1|1].value) % MOD;
}
int Calc(int a, int times)
{
for(int i=times; i>=1; i--)
{
if(a >= phi[i]) a = a%phi[i] + phi[i];
a = Quickpow(C, a, phi[i-1]);
if(!a) a = phi[i-1];
}
return a;
}
void Update(int i,int l,int r,int L,int R)
{
if(Node[i].cnt >= p_num) return;
if(l == r)
{
Node[i].value = Calc(a[l], ++Node[i].cnt);
return;
}
int mid = l+r>>1;
if(L <= mid) Update(i<<1, l, mid, L, R);
if(mid+1 <= R) Update(i<<1|1, mid+1, r, L, R);
Node[i].value = (Node[i<<1].value + Node[i<<1|1].value) % MOD;
Node[i].cnt = min(Node[i<<1].cnt, Node[i<<1|1].cnt);
}
void Query(int i,int l,int r,int L,int R)
{
if(L<=l && r<=R)
{
res = (res + Node[i].value) % MOD;
return;
}
int mid = l+r>>1;
if(L <= mid) Query(i<<1, l, mid, L, R);
if(mid+1 <= R) Query(i<<1|1, mid+1, r, L, R);
}
int main()
{
n = get(); m = get(); p = get(); C = get();
for(int i=1; i<=n; i++) a[i] = get();
MOD = phi[0] = p;
while(p!=1) phi[++p_num] = p = Getphi(p);
phi[++p_num] = 1;
Build(1, 1, n);
while(m--)
{
opt = get();
x = get(); y = get();
if(!opt) Update(1, 1, n, x, y);
else
{
res = 0;
Query(1, 1, n, x, y);
printf("%d\n", res);
}
}
}
View Code
【BZOJ4869】相逢是問候 [線段樹]

