HDU 2489 Minimal Ratio Tree (dfs+Prim最小生成樹)
阿新 • • 發佈:2017-06-03
tracking mode pid cas cond multi ima ces bold
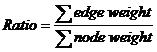
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
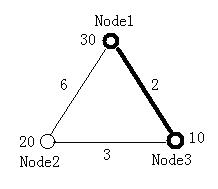
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
Output For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there‘s a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 . Sample Input
題目鏈接:http://acm.hdu.edu.cn/showproblem.php?pid=2489
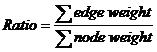
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there‘s a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 . Sample Input
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
1 3 1 2Source 2008 Asia Regional Beijing
題意:
給出n個點。要從中選出m個點。要求選出的這m個點的全部邊的邊權值/點權值要最小!
並要輸出所選的這m個點,假設有多種選擇方法,那麽就輸出第一個點小的方案,假設第一個點同樣就輸出第二個點小的,一次類推!
PS:
因為這題的n比較小,僅僅有15。所以能夠先dfs枚舉出所選擇的點。然後在用最小生成樹Prim算出最小的邊權值的和。
代碼例如以下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
#define INF 1e18;
const double eps = 1e-9;
const int maxn = 17;
int n, m;
int e_val[maxn][maxn];
int node[maxn];
int ansn[maxn];//記錄終於選得是哪些點
int tt[maxn];//記錄中間過程選得是哪些點
int vis[maxn];
int low[maxn];
double minn;
int Prim(int s)
{
int sum=0;
memset(vis,0,sizeof(vis));
for(int i = 1; i <= m; i++)
{
low[tt[i]] = e_val[s][tt[i]];
}
vis[s] = 1;
low[s] = 0;
int pos = s;
for(int i = 1; i < m; i++)
{
int min_t = INF;
for(int j = 1; j <= m; j++)
{
if(!vis[tt[j]] && min_t > low[tt[j]])
{
min_t = low[tt[j]];
pos = tt[j];
}
}
vis[pos] = 1;
sum += min_t;
for(int j = 1; j <= m; j++)
{
if(!vis[tt[j]] && e_val[pos][tt[j]] < low[tt[j]])
low[tt[j]]=e_val[pos][tt[j]];
}
}
return sum;
}
void DFS(int n_pre, int k)
{
if(k == m)
{
double n_sum = 0;
for(int i = 1; i <= m ; i++)
{
n_sum+=node[tt[i]];
}
double e_ans = 0;
e_ans = Prim(tt[1]);
double ans = e_ans/(n_sum*1.0);
//if(ans < minn)
if(ans - minn < -(eps))
{
minn = ans;
for(int i = 1; i <= m; i++)
{
ansn[i] = tt[i];
}
}
return ;
}
for(int i = n_pre+1; i <= n; i++)
{
tt[k+1] = i;
DFS(i,k+1);
}
}
int main()
{
while(~scanf("%d%d",&n,&m))
{
if(n==0 && m==0)
break;
minn = INF;
for(int i = 1; i <= n; i++)
{
scanf("%d",&node[i]);
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
scanf("%d",&e_val[i][j]);
}
}
for(int i = 1; i <= n; i++)
{
tt[1] = i;
DFS(i, 1);
}
for(int i = 1; i < m; i++)
{
printf("%d ",ansn[i]);
}
printf("%d\n",ansn[m]);
}
return 0;
}
HDU 2489 Minimal Ratio Tree (dfs+Prim最小生成樹)
