HDU-2489 Minimal Ratio Tree(最小生成樹)
阿新 • • 發佈:2017-09-24
figure tro line accep tree one 分享 origin regional
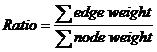
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
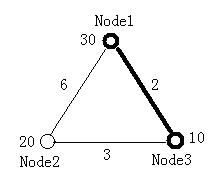
Minimal Ratio Tree
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4610 Accepted Submission(s):
1466
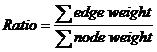
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there‘s a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 .
Sample Output 1 3 1 2
Source 2008 Asia Regional Beijing
Recommend
1 #include "bits/stdc++.h" 2 using namespace std; 3 typedef long long LL; 4 const int MAX=20; 5 int n,m; 6 int a[MAX],b[MAX][MAX],c[MAX]; 7 int ans[MAX];double an; 8 struct Edge{ 9 int u,v; 10 int w; 11 bool operator < (const Edge &tt) const { 12 return w<tt.w; 13 } 14 }edge[MAX*MAX]; 15 int fa[MAX]; 16 int getfather(int x){ 17 if (fa[x]==x) return x; 18 return fa[x]=getfather(fa[x]); 19 } 20 void dfs(int no,int now){ 21 int i,j; 22 if (now==m+1){ 23 int x=0,y=0; 24 for (i=1;i<=m;i++){y+=a[c[i]];} 25 for (i=1;i<=n;i++){fa[i]=i;} 26 int len=0; 27 for (i=1;i<=m;i++){ 28 for (j=i+1;j<=m;j++){ 29 edge[++len].u=c[i]; 30 edge[len].v=c[j]; 31 edge[len].w=b[c[i]][c[j]]; 32 } 33 } 34 sort(edge+1,edge+len+1); 35 for (i=1;i<=len;i++){ 36 int dx=getfather(edge[i].u); 37 int dy=getfather(edge[i].v); 38 if (dx!=dy){ 39 x+=edge[i].w; 40 fa[dx]=dy; 41 } 42 } 43 double xy=(x*1.0)/(y*1.0); 44 if (xy<an){ 45 for (i=1;i<=m;i++) 46 ans[i]=c[i]; 47 an=xy; 48 } 49 } 50 for (i=no+1;i<=n;i++){ 51 c[now]=i; 52 dfs(i,now+1); 53 } 54 } 55 int main(){ 56 int i,j; 57 while (1){ 58 scanf("%d%d",&n,&m);if (n==0 && m==0) break; 59 an=100000000.0; 60 for (i=1;i<=n;i++){ 61 scanf("%d",a+i); 62 } 63 for (i=1;i<=n;i++){ 64 for (j=1;j<=n;j++){ 65 scanf("%d",&b[i][j]); 66 } 67 } 68 dfs(0,1); 69 sort(ans+1,ans+m+1); 70 for (i=1;i<m;i++){ 71 printf("%d ",ans[i]); 72 } 73 printf("%d\n",ans[m]); 74 } 75 return 0; 76 }
HDU-2489 Minimal Ratio Tree(最小生成樹)
