一、線性濾波與卷積的基本概念

線性濾波可以說是圖像處理最基本的方法，它可以允許我們對圖像進行處理，產生很多不同的效果。做法很簡單。首先，我們有一個二維的濾波器矩陣（有個高大上的名字叫卷積核）和一個要處理的二維圖像。然後，對於圖像的每一個像素點，計算它的鄰域像素和濾波器矩陣的對應元素的乘積，然後加起來，作為該像素位置的值。這樣就完成了濾波過程。

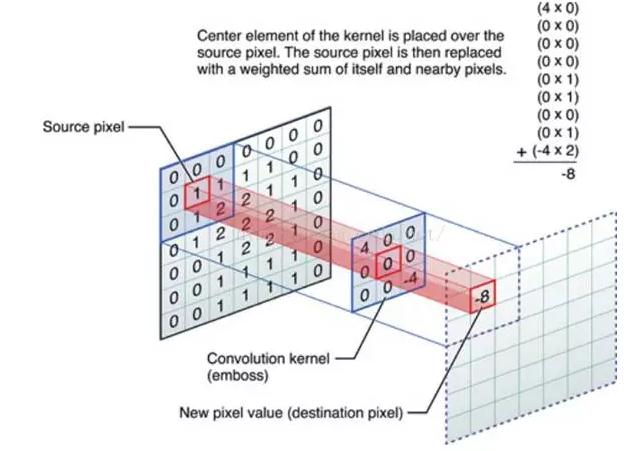
對圖像和濾波矩陣進行逐個元素相乘再求和的操作就相當於將一個二維的函數移動到另一個二維函數的所有位置，這個操作就叫卷積或者協相關。卷積和協相關的差別是，卷積需要先對濾波矩陣進行180的翻轉，但如果矩陣是對稱的，那麽兩者就沒有什麽差別了。

Correlation 和 Convolution可以說是圖像處理最基本的操作，但卻非常有用。這兩個操作有兩個非常關鍵的特點：它們是線性的，而且具有平移不變性shift-invariant。平移不變性指我們在圖像的每個位置都執行相同的操作。線性指這個操作是線性的，也就是我們用每個像素的鄰域的線性組合來代替這個像素。這兩個屬性使得這個操作非常簡單，因為線性操作是最簡單的，然後在所有地方都做同樣的操作就更簡單了。

實際上，在信號處理領域，卷積有廣泛的意義，而且有其嚴格的數學定義，但在這裏不關註這個。

2D卷積需要4個嵌套循環4-double loop，所以它並不快，除非我們使用很小的卷積核。這裏一般使用3x3或者5x5。而且，對於濾波器，也有一定的規則要求：

1）濾波器的大小應該是奇數，這樣它才有一個中心，例如3x3，5x5或者7x7。有中心了，也有了半徑的稱呼，例如5x5大小的核的半徑就是2。

2）濾波器矩陣所有的元素之和應該要等於1，這是為了保證濾波前後圖像的亮度保持不變。當然了，這不是硬性要求了。

3）如果濾波器矩陣所有元素之和大於1，那麽濾波後的圖像就會比原圖像更亮，反之，如果小於1，那麽得到的圖像就會變暗。如果和為0，圖像不會變黑，但也會非常暗。

4）對於濾波後的結構，可能會出現負數或者大於255的數值。對這種情況，我們將他們直接截斷到0和255之間即可。對於負數，也可以取絕對值。

二、神奇的卷積核

上面說到，對圖像的濾波處理就是對圖像應用一個小小的卷積核，那這個小小的卷積核到底有哪些魔法，能讓一個圖像從慘不忍睹變得秀色可餐。下面我們一起來領略下一些簡單但不簡單的卷積核的魔法。

2.1、啥也不做

哈哈，大家可以看到啥了嗎？這個濾波器啥也沒有做，得到的圖像和原圖是一樣的。因為只有中心點的值是1。鄰域點的權值都是0，對濾波後的取值沒有任何影響。

下面我們動點真格的。

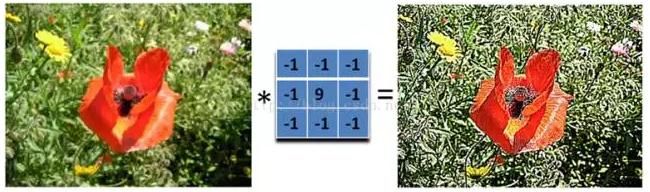
2.2、圖像銳化濾波器Sharpness Filter

圖像的銳化和邊緣檢測很像，首先找到邊緣，然後把邊緣加到原來的圖像上面，這樣就強化了圖像的邊緣，使圖像看起來更加銳利了。這兩者操作統一起來就是銳化濾波器了，也就是在邊緣檢測濾波器的基礎上，再在中心的位置加1，這樣濾波後的圖像就會和原始的圖像具有同樣的亮度了，但是會更加銳利。

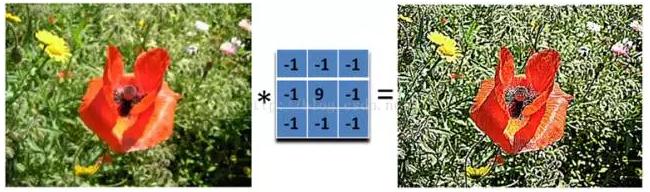
我們把核加大，就可以得到更加精細的銳化效果

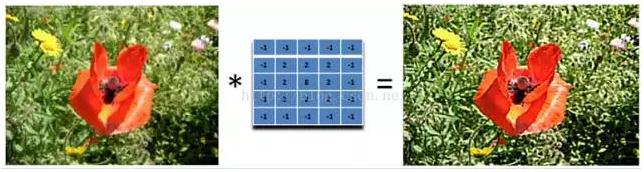
另外，下面的濾波器會更強調邊緣：

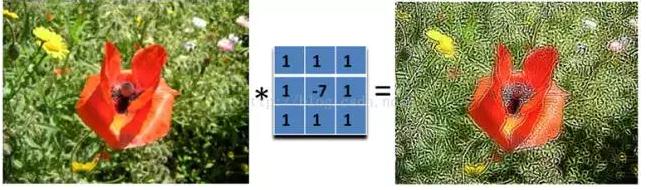
主要是強調圖像的細節。最簡單的3x3的銳化濾波器如下：

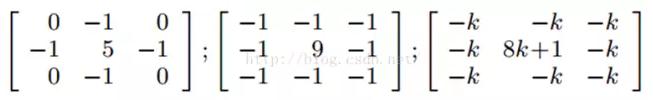
實際上是計算當前點和周圍點的差別，然後將這個差別加到原來的位置上。另外，中間點的權值要比所有的權值和大於1，意味著這個像素要保持原來的值。

2.3、邊緣檢測Edge Detection

我們要找水平的邊緣：需要註意的是，這裏矩陣的元素和是0，所以濾波後的圖像會很暗，只有邊緣的地方是有亮度的。

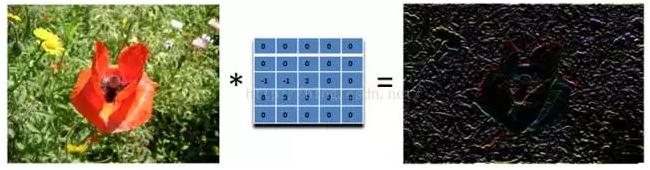
為什麽這個濾波器可以尋找到水平邊緣呢？因為用這個濾波器卷積相當於求導的離散版本：你將當前的像素值減去前一個像素值，這樣你就可以得到這個函數在這兩個位置的差別或者斜率。下面的濾波器可以找到垂直方向的邊緣，這裏像素上和下的像素值都使用：

再下面這個濾波器可以找到45度的邊緣：取-2不為了什麽，只是為了讓矩陣的元素和為0而已。

那下面這個濾波器就可以檢測所有方向的邊緣:

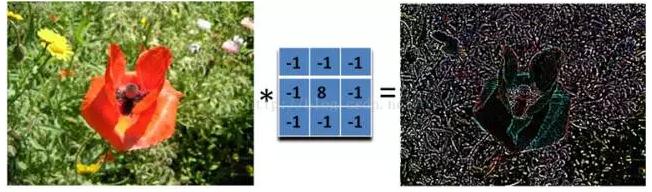
為了檢測邊緣，我們需要在圖像對應的方向計算梯度。用下面的卷積核來卷積圖像，就可以了。但在實際中，這種簡單的方法會把噪聲也放大了。另外，需要註意的是，矩陣所有的值加起來要是0.

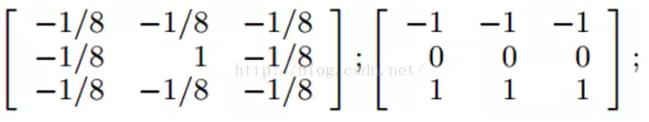
2.4、浮雕Embossing Filter

浮雕濾波器可以給圖像一種3D陰影的效果。只要將中心一邊的像素減去另一邊的像素就可以了。這時候，像素值有可能是負數，我們將負數當成陰影，將正數當成光，然後我們對結果圖像加上128的偏移。這時候，圖像大部分就變成灰色了。

下面是45度的浮雕濾波器

我們只要加大濾波器，就可以得到更加誇張的效果了

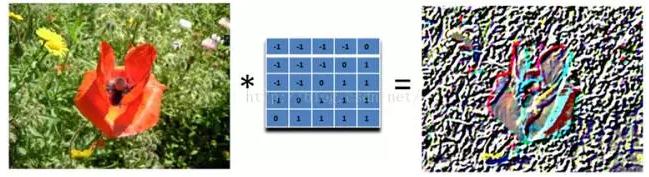
這種效果非常的漂亮，就像是將一副圖像雕刻在一塊石頭上面一樣，然後從一個方向照亮它。它和前面的濾波器不同，它是非對稱的。另外，它會產生負數值，所以我們需要將結果偏移，以得到圖像灰度的範圍。

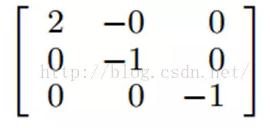
A：原圖像。B：銳化。C：邊緣檢測。D：浮雕

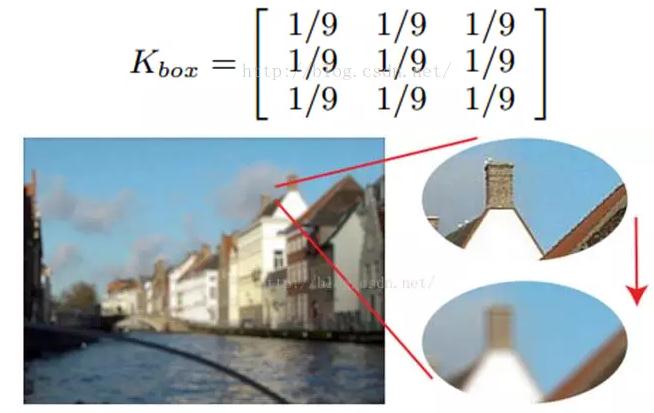
2.5、均值模糊Box Filter (Averaging)

我們可以將當前像素和它的四鄰域的像素一起取平均，然後再除以5，或者直接在濾波器的5個地方取0.2的值即可，如下圖：

可以看到，這個模糊還是比較溫柔的，我們可以把濾波器變大，這樣就會變得粗暴了：註意要將和再除以13.

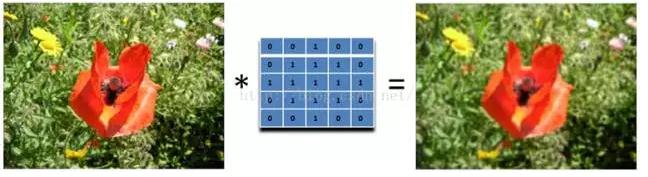
所以，如果你想要更模糊的效果，加大濾波器的大小即可。或者對圖像應用多次模糊也可以。

2.6、高斯模糊

均值模糊很簡單，但不是很平滑。高斯模糊就有這個優點，所以被廣泛用在圖像降噪上。特別是在邊緣檢測之前，都會用來移除細節。高斯濾波器是一個低通濾波器。

2.7、運動模糊Motion Blur

運動模糊可以通過只在一個方向模糊達到，例如下面9x9的運動模糊濾波器。註意，求和結果要除以9。

這個效果就好像，攝像機是從左上角移動的右下角。

三、卷積的計算

對圖像處理而言，存在兩大類的方法：空域處理和頻域處理！空域處理是指直接對原始的像素空間進行計算，頻率處理是指先對圖像變換到頻域，再做濾波等處理。

3.1、空域計算-直接2D卷積

3.1.1、2D卷積

直接2D卷積就是一開始說的那樣，對於圖像的每一個像素點，計算它的鄰域像素和濾波器矩陣的對應元素的乘積，然後加起來，作為該像素位置的值。

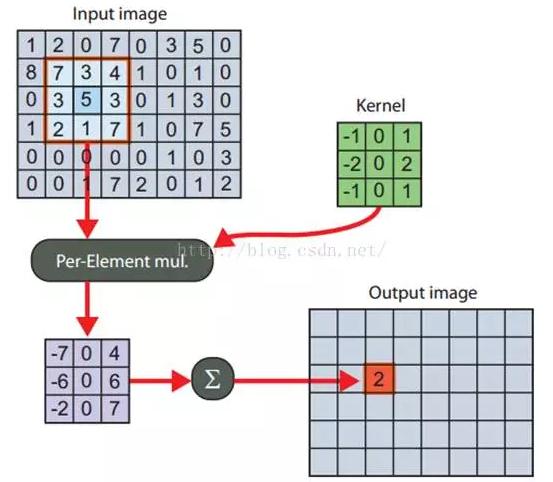
直接的實現也稱為暴力實現brute force，因為它嚴格按照定義來實現，沒有任何優化。當然了，在並行實現裏面，它也是比較靈活的。另外，也存在一個優化版本，如果我們的kernel是separable可分的，那麽就可以得到一個快5倍左右的卷積方法。

2.1.2、邊界處理

那卷積核遇到圖像邊緣怎麽辦？例如圖像頂部的像素，它的上面已經沒有像素了，那麽它的值如何計算？目前有四種主流的處理方法，我們用一維卷積和均值濾波來說明下。

我們在1D圖像中，用每個像素和它的二鄰域的平均值來取代它的值。假設我們有個1D的圖像I是這樣的：

對非圖像邊界的像素的操作比較簡單。假設我們對I的第四個像素3做局部平均。也就是我們用2,3和7做平均，來取代這個位置的像素值。也就是，平均會產生一副新的圖像J，這個圖像在相同位置J (4) = (I(3)+I(4)+I(5))/3 = (2+3+7)/3 = 4。同樣，我們可以得到J(3) = (I(2)+I(3)+I(4))/3 =(4+2+3)/3 = 3。需要註意的是，新圖像的每個像素都取決於舊的圖像，在計算J (4)的時候用J (3)是不對的，而是用I(3)，I(4)和I(5)。所以每個像素都是它和它鄰域兩個像素的平均。平均是線性的操作，因為每個新的像素都是舊像素的線性組合。

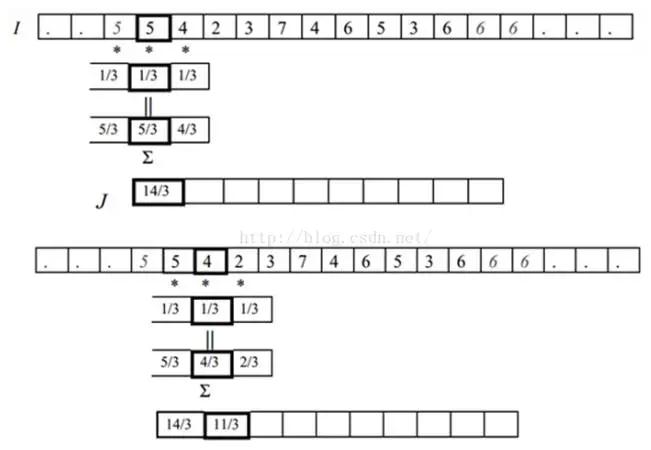
對卷積，也有必須要考慮的情況是，在圖像邊界的時候，怎麽辦？J(1)的值應該是什麽？它取決於I(0)，I(1)和I(2)。但是我們沒有I(0)呀！圖像左邊沒有值了。有四種方式來處理這個問題：

1）第一種就是想象I是無限長的圖像的一部分，除了我們給定值的部分，其他部分的像素值都是0。在這種情況下，I(0)=0。所以J(1) = (I(0) + I(1) + I(2))/3 = (0 + 5 + 4)/3= 3. 同樣，J(10) = (I(9)+I(10)+I(11))/3 = (3+ 6 + 0)/3 = 3.

2）第二種方法也是想象I是無限圖像的一部分。但沒有指定的部分是用圖像邊界的值進行拓展。在我們的例子中，因為圖像I最左邊的值I(1)=5，所以它左邊的所有值，我們都認為是5 。而圖像右邊的所有的值，我們都認為和右邊界的值I(10)一樣，都是6。這時候J(1) = (I(0) + I(1) + I(2))/3 = (5 + 5 + 4)/3= 14/3. 而J(10) = (I(9)+I(10)+I(11))/3 = (3 + 6 + 6)/3 = 5。

3）第三種情況就是認為圖像是周期性的。也就是I不斷的重復。周期就是I的長度。在我們這裏，I(0)和I(10)的值就是一樣的，I(11)的值和I(1)的值也是一樣的。所以J(1) = (I(0) + I(1) + I(2))/3= (I(10) + I(1)+ I(2))/3 = (6 + 5 + 4)/3 = 5 。

4）最後一種情況就是不管其他地方了。我們覺得I之外的情況是沒有定義的，所以沒辦法使用這些沒有定義的值，所以要使用圖像I沒有定義的值的像素都沒辦法計算。在這裏，J(1)和J(10)都沒辦法計算，所以輸出J會比原圖像I要小。

這四種方法有各自的優缺點。如果我們想象我們使用的圖像只是世界的一個小窗口，然後我們需要使用窗口邊界外的值，那麽一般來說，外面的值和邊界上的值是幾乎相似的，所以第二種方法可能更說得過去。

2.2、頻域計算-快速傅裏葉變換FFT卷積

這個快速實現得益於卷積定理：時域上的卷積等於頻域上的乘積。所以將我們的圖像和濾波器通過算法變換到頻域後，直接將他們相乘，然後再變換回時域（也就是圖像的空域）就可以了。

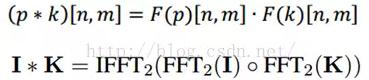
o表示矩陣逐元素相乘。那用什麽方法將空域的圖像和濾波器變換到頻域了。那就是鼎鼎大名的Fast Fourier Transformation 快速傅裏葉變換FFT（其實，在CUDA裏面，已經實現了FFT了）。

要在頻域中對一副圖像進行濾波，濾波器的大小和圖像的大小必須要匹配，這樣兩者的相乘才容易。因為一般濾波器的大小比圖像要小，所以我們需要拓展我們的kernel，讓它和圖像的大小一致。

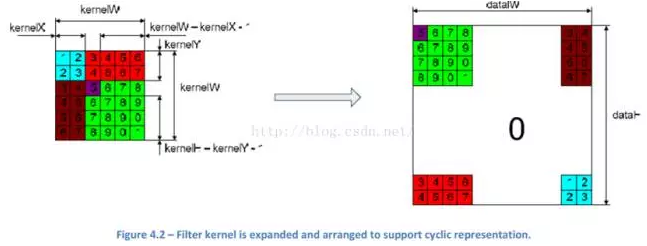
因為CUDA中的FFT實現是周期的，所以kernel的值也要安排成這樣，以支持這種周期性。

為了保證圖像邊界的像素也可以得到響應輸出，我們也需要拓展我們的輸入圖像。同時，拓展的方式也要支持周期表達。

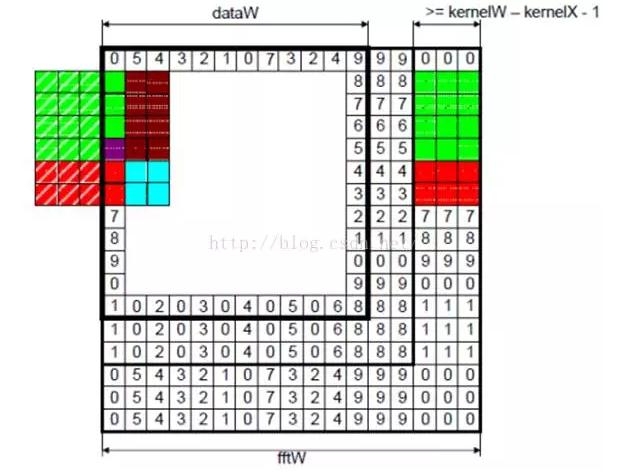
如果只是使用卷積定理，沒有對輸入進行任何修改的話，那麽我們得到的是周期卷積的結果。但這可能不是我們要的，因為周期卷積會對輸入數據進行周期填補，引入一些artifacts。

給定N長度的I和K，為了得到線性卷積，我們需要對I和K進行zero padding。為什麽要補0，因為DFT假定了輸入是無限和周期的，周期是N。　

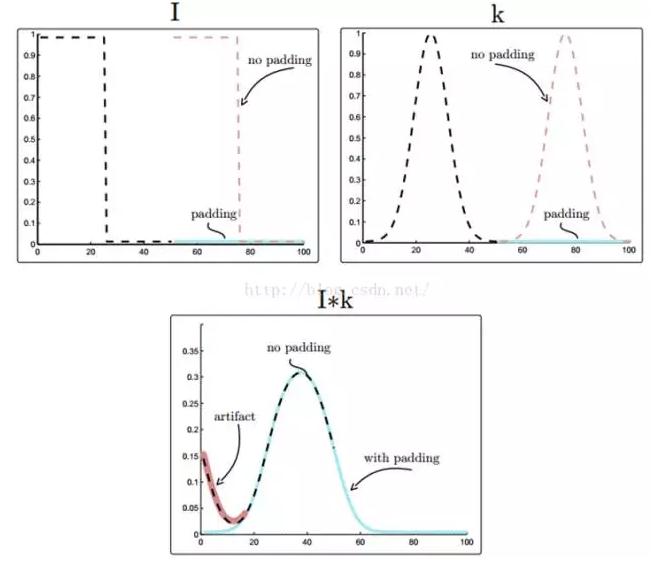
如上圖，對於I和K，如果沒有padding的話，隱含著會假定I和K是周期的，以他們的長度N為周期。圖中本來N長度的I和K都是黑色虛線的部分，然後如果沒有padding，隱含著就會在N之外，加上同樣的無數個I，如紅色虛線部分，加上了一個周期。對K也是這樣。如果是zero padding的話，在黑色虛線的其他地方都全是0了，如圖中藍色部分。將I和K卷積，如果沒有padding，如黑色虛線，會有紅色那部分的artifact。如果有padding，就是藍色實線。

四、實驗代碼

這是第二部分的Matlab實驗代碼：

clear,close all, clc

%% readimage

image =imread(‘test.jpg‘);

%% definefilter

% -----Identity filter -----

kernel =[0, 0, 0

0, 1, 0

0, 0, 0];

% -----Average Blur -----

kernel =[0, 1, 0

1, 1, 1

0, 1, 0] / 5;

% -----Gaussian Blur -----

kernel =fspecial(‘gaussian‘, 5 , 0.8);

% -----Motion Blur -----

kernel =[1, 0, 0, 0, 0

0, 1, 0, 0, 0

0, 0, 1, 0, 0

0, 0, 0, 1, 0

0, 0, 0, 0, 1] / 5;

% -----Edges Detection -----

kernel =[-1, -1, -1

-1, 8, -1

-1, -1, -1];

% -----Sharpen filter -----

kernel =[-1, -1, -1

-1, 9, -1

-1, -1, -1];

% -----Emboss filter -----

kernel =[-1, -1, 0

-1, 0,1

0, 1,1];

%% convolethe image with defined kernel or filter

result =zeros(size(image));

result(:,:, 1) = conv2(double(image(:, :, 1)), double(kernel), ‘same‘);

result(:,:, 2) = conv2(double(image(:, :, 2)), double(kernel), ‘same‘);

result(:,:, 3) = conv2(double(image(:, :, 3)), double(kernel), ‘same‘);

%% showthe result

imshow(image);

figure

imshow(uint8(result))

圖像卷積與濾波