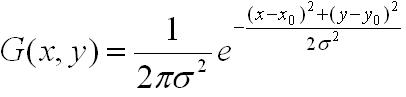轉載地址  http://blog.csdn.net/dcrmg/article/details/52304446#reply

http://blog.csdn.net/yangyangyang20092010/article/details/48576007  也對高斯權值做了詳細的解釋

高斯濾波是一種線性平滑濾波，適用於消除高斯噪聲，在影象處理的降噪、平滑中應用較多，特別是對抑制或消除服從正態分佈的噪聲非常有效。

高斯濾波的過程其實就是對整幅影象進行加權平均操作的過程。濾波後圖像上每一個畫素的灰度值大小，由其本身和鄰域內的其他畫素共同決定。具體實現是：用一個大小為（2*N+1）的模板（或稱卷積核、掩模）依次掃描影象中的每一個畫素，用模板確定的鄰域內畫素的加權平均灰度替代模板中心畫素點的灰度值。

一維、二維高斯分佈

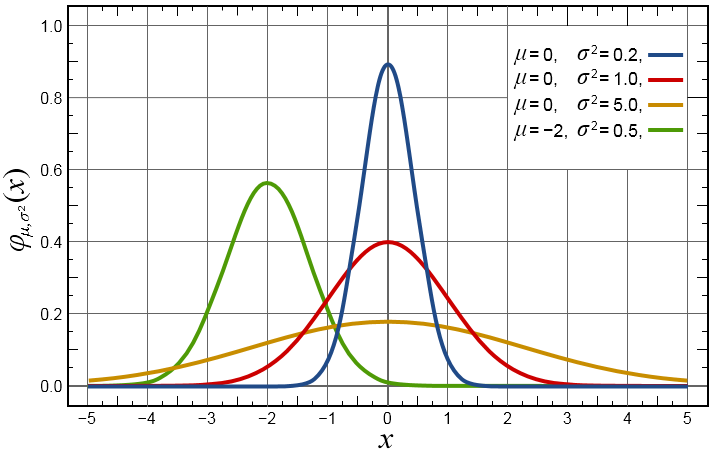
一維高斯函式表述為：

對應圖形：

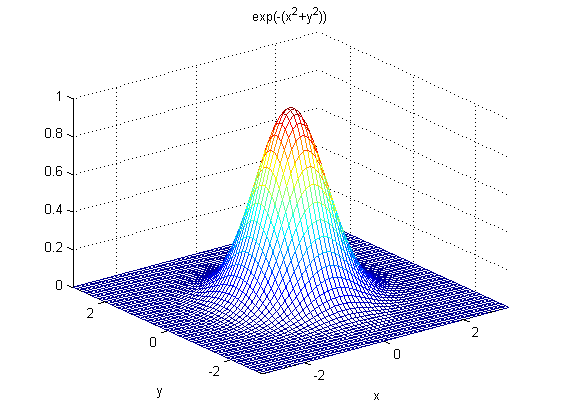
二維高斯函式表述為：

對應圖形：

一些重要特性說明：

1. 一維二維高斯函式中μ是服從正態分佈的隨機變數的均值，稱為期望或均值影響正態分佈的位置，實際的影象處理應用中一般取μ=0；σ是標準差，σ^2是隨機變數的方差，σ定義了正態分佈資料的離散程度，σ越大，資料分佈越分散，σ越小，資料分佈越集中。

在圖形或濾波效果上表現為：σ越大，曲線越扁平，高斯濾波器的頻帶就越寬，平滑程度就越好，σ越小，曲線越瘦高，高斯濾波的頻帶就越窄，平滑程度也越弱；

2. 二維高斯函式具有旋轉對稱性，即濾波器在各個方向上的平滑程度是相同的．一般來說，一幅影象的邊緣方向是事先不知道的，因此，在濾波前是無法確定一個方向上比另一方向上需要更多的平滑．旋轉對稱性意味著高斯平滑濾波器在後續邊緣檢測中不會偏向任一方向；

3. 高斯函式是單值函式。這表明，高斯濾波器用畫素鄰域的加權均值來代替該點的畫素值，而每一鄰域畫素點權值是隨該點與中心點的距離單調增減的。這一性質是很重要的，因為邊緣是一種影象區域性特徵，如果平滑運算對離運算元中心很遠的畫素點仍然有很大作用，則平滑運算會使影象失真；

4.  相同條件下，高斯卷積核的尺寸越大，影象的平滑效果越好，表現為影象越模糊，同時影象細節丟失的越多；尺寸越小，平滑效果越弱，影象細節丟失越少；

以下對比一下不同大小標準差σ（Sigma）對影象平滑的影響：

原圖：

卷積核尺寸5*5，σ=0.1：

卷積核尺寸5*5，σ=1：

對比可以看到，Sigma(σ)越大，平滑效果越明顯。

C++對高斯卷積核引數求解：

1. #include "iostream"  
2. #include "math.h"  
3.   
4. using namespace std;   
5. using namespace cv;    
6.   
7. //******************高斯卷積核生成函式*************************  
8. //第一個引數gaus是一個指向含有3個double型別陣列的指標；  
9. //第二個引數size是高斯卷積核的尺寸大小；  
10. //第三個引數sigma是卷積核的標準差  
11. //*************************************************************  
12. void GetGaussianKernel(double **gaus, const int size,const double sigma);  
13.   
14. int main(int argc,char *argv[])    
15. {  
16.     int size=5; //定義卷積核大小  
17.     double **gaus=new double *[size];  
18.     for(int i=0;i<size;i++)  
19.     {  
20.         gaus[i]=new double[size];  //動態生成矩陣  
21.     }  
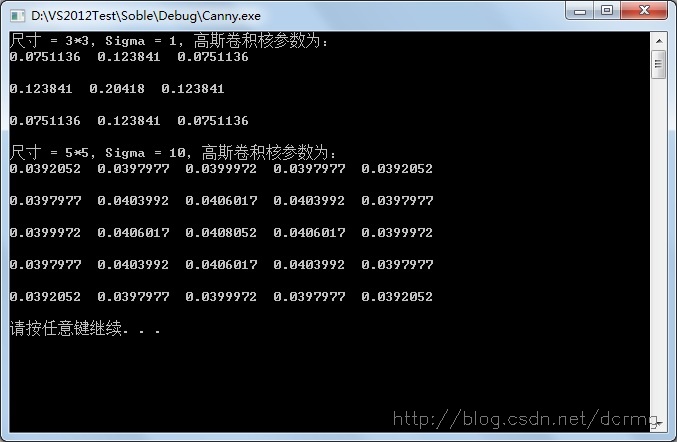
22.     cout<<"尺寸 = 3*3，Sigma = 1，高斯卷積核引數為："<<endl;  
23.     GetGaussianKernel(gaus,3,1); //生成3*3 大小高斯卷積核，Sigma=1；     
24.     cout<<"尺寸 = 5*5，Sigma = 10，高斯卷積核引數為："<<endl;  
25.     GetGaussianKernel(gaus,5,10); //生成5*5 大小高斯卷積核，Sigma=1；    
26.     system("pause");  
27.     return 0;  
28. }  
29.   
30. //******************高斯卷積核生成函式*************************  
31. void GetGaussianKernel(double **gaus, const int size,const double sigma)  
32. {  
33.     const double PI=4.0*atan(1.0); //圓周率π賦值  
34.     int center=size/2;  
35.     double sum=0;  
36.     for(int i=0;i<size;i++)  
37.     {  
38.         for(int j=0;j<size;j++)  
39.         {  
40.             gaus[i][j]=(1/(2*PI*sigma*sigma))*exp(-((i-center)*(i-center)+(j-center)*(j-center))/(2*sigma*sigma));  
41.             sum+=gaus[i][j];  
42.         }  
43.     }  
44.   
45.     for(int i=0;i<size;i++)  
46.     {  
47.         for(int j=0;j<size;j++)  
48.         {  
49.             gaus[i][j]/=sum;  
50.             cout<<gaus[i][j]<<"  ";  
51.         }  
52.         cout<<endl<<endl;  
53.     }  
54.     return ;  
55. }  

求得的高斯卷積核引數存放在一個大小為N*N的陣列內：