二叉搜索樹
--------------------siwuxie095
二叉搜索樹
這裏介紹二叉搜索樹(Binary Search Tree)
二叉搜索樹,顧名思義,本質上也是一棵二叉樹
二叉樹在計算機中是一種非常常用的數據結構,選擇什麽類型的二叉樹
很多時候要根據需要解決的問題而定
使用數據結構的核心是要解決問題,而並非是為了使用數據結構而使用
數據結構
使用二叉樹並不是因為二叉樹很酷,很炫,聽起來很專業,而是因為二
叉樹能夠高效的解決一類問題
二叉搜索樹解決的一類問題就是在計算機中非常常見的
「查找問題是計算機中非常重要的基礎問題」
可能很多人會覺得這個問題非常簡單,就是在一組數據中找到某
個數據,但是仔細想一想就會發現,查找問題雖然描述出來很簡
單,但是它的應用卻非常廣泛
從去銀行辦理業務時,銀行根據證件號碼從系統中調出相應的信
息,到在 Google 中搜索內容時,Google 根據關鍵字來查找相
關的信息 …
查找問題,是一個聽起來非常樸素,實際上卻非常困難,被研究
的非常廣泛的一類問題
「查找問題,即 Search Problem」
二叉搜索樹的優勢
事實上,二叉搜索樹,通常都用於實現
有的地方,也稱 查找表 為 字典,如下:
key1 | value1 |
key2 | value2 |
key3 | value3 |
key4 | value4 |
key5 | value5 |
即 對於這些數據而言,都是一個一個鍵值對,即 key-value
對應的數據對,給你一個 key,相應的就有一個 value
這樣大量的數據對,集合在一起就形成了一張表,在這張表
中通過鍵(key)就能直接查到對應的值(value)
最典型的一個應用就是字典。對於一個字典來說,鍵(key)
就是一個個單詞,而值(value)就是單詞的釋義
這也是查找表有時候也被稱為字典這樣一種數據結構的原因
如果這些 key 都是整數,而且範圍比較小,那麽使用數組就可以輕易
地用索引直接來索引到相應的 value
但在實際的業務邏輯中,很多時候不能用整數來表達這樣的鍵(key),
或者是因為這些鍵(key)相對比較稀疏,使用數組在空間上並不經濟,
或者是因為這些鍵(key)壓根就不能用整數來表示
例如:字典的鍵(key)其實是一個字符串
這種情況下,就需要實現一個查找表,而實現查找表的最基礎的一個
方式是實現二叉搜索樹
當然,也完全可以用 普通數組 或 順序數組 來實現這個一個查找表
| 查找元素 | 插入元素 | 刪除元素 |
普通數組 | O(n) | O(n) | O(n) |
順序數組 | O(lgn) | O(n) | O(n) |
二分搜索樹 | O(lgn) | O(lgn) | O(lgn) |
可以簡單分析一下使用普通數組 或 順序數組的時間效率:
1)使用普通數組:
查找一個元素,就需要使用 O(n) 的時間從頭到尾遍歷一遍,看要找的
那個元素在數組的什麽位置
插入一個元素,也需要使用 O(n) 的時間從頭到尾遍歷一遍,因為對於
查找表來說,需要先看一看當前查找表中是否已經含有要插入的元素。
如果沒有,再插入;如果有的話,就應該是對 key 相應的 value 進行
一個更新操作
刪除一個元素,也需要使用 O(n) 的時間從頭到尾遍歷一遍,來刪除相
應的元素
2)使用順序數組:
要一直保證這個數組是有序的。這樣一來,查找一個元素就可以使用
二分查找法,用 O(lgn) 的時間進行查找,但對於插入一個元素和刪除
一個元素來說,依然要使用 O(n) 的時間
相較而言,二叉搜索樹就高效很多,它能夠保證查找、插入、刪除這
三個操作的時間復雜度近乎都是 O(lgn) 級別的
所以,二叉搜索樹的優勢:
1)高效
不僅可以高效查找數據,還可以高效地插入數據、刪除數據 - 動態維護數據
也就是說,如果能一下就把所有的數據拿到手,那可能先對數據進行排序再
使用二分查找法,就足夠了
但在很多時候,查找、插入、刪除這三個操作,在業務的過程中都是要涉及
的,因此,二叉搜索樹提供了一個可以非常高效地動態維護數據的方式
2)可以方便地回答很多數據之間的關系問題,如下:
min、max、floor、ceil、rank、select
可以輕易地找到所有數據中的最小值 min、最大值 max,某個數據的 floor
相應的值、ceil 相應的值,還有給定一個數據,求它的排名 rank,以及找
到所有數據中某排名(如:第 100 名)的數據 select
二叉搜索樹的定義
如下圖所示,是一棵二叉搜索樹:
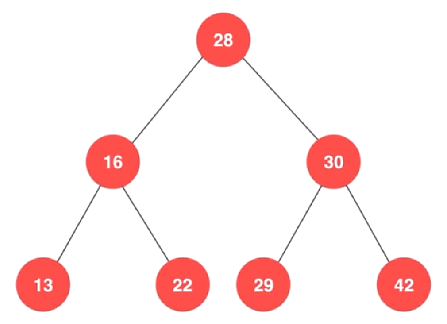
二叉搜索樹,是指一棵空樹 或者具有下列性質的二叉樹:
1)若任意節點的左子樹不空,則左子樹上所有結點的值均小於它的根結點的值
2)若任意節點的右子樹不空,則右子樹上所有結點的值均大於它的根結點的值
3)任意節點的左、右子樹也分別為二叉搜索樹
4)沒有鍵值相等的節點
即
1)每個節點的鍵值都大於左孩子
2)每個節點的鍵值都小於右孩子
不難看出,二叉搜索樹的定義中天然就包含了遞歸結構
正因為如此,在對二叉搜索樹編程時,很多時候都可以使用遞歸函數的方式,
方便快速地實現很多功能
註意:對於堆來說,堆的那棵二叉樹一定是一棵完全二叉樹,但對於二叉搜索
樹來說,是沒有這個限制的,如下:
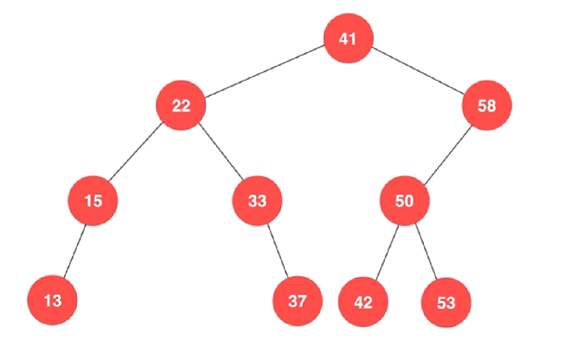
換句話說,上圖中的這棵樹,也是二叉搜索樹,即 二叉搜索樹,不一定是
完全二叉樹
在實現堆的時候,是利用了堆一定是一棵完全叉樹的特點,所以能用數組
來表示堆,但二分搜索樹不一定是完全二叉樹,所以用數組表示並不方便
因此,通常是設立 Node 節點,來表示 key-value 這樣的數據對,而節點
之間的聯系,則使用指針的方式來表示
【made by siwuxie095】
二叉搜索樹
