【BZOJ3944/4805】Sum/歐拉函數求和 杜教篩
阿新 • • 發佈：2017-06-13
width pri define second pair ring 空格 string pll
1
2
8
13
30
2333
2 0
22 -2
58 -3
278 -3
1655470 2
【BZOJ3944】Sum
Description
Input
一共T+1行 第1行為數據組數T(T<=10) 第2~T+1行每行一個非負整數N，代表一組詢問Output
一共T行，每行兩個用空格分隔的數ans1,ans2Sample Input
61
2
8
13
30
2333
Sample Output
1 12 0
22 -2
58 -3
278 -3
1655470 2
題解：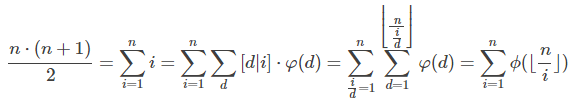
粘自http://blog.csdn.net/skywalkert/article/details/50500009
求莫比烏斯函數的前綴和類似，從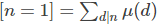
開始推就好了
#include <cstdio>
#include <cstring>
#include <iostream>
#include <map>
#include <utility>
#define MP(A,B) make_pair(A,B)
using namespace std;
const int m=3000000;
typedef long long ll;
int n,num;
ll phi[m+10],mu[m+10],sp[m+10],sm[m+10],pri[m+10];
bool np[m+10];
typedef pair<ll,ll> pll;
map<ll,pll> mp;
pll dfs(ll x)
{
if(x<=m) return MP(sp[x],sm[x]);
if(mp.find(x)!=mp.end()) return MP(mp[x].first,mp[x].second);
ll rp=x*(x+1)>>1,rm=1,i,last;
for(i=2;i<=x;i=last+1)
{
last=x/(x/i);
pll tmp=dfs(x/i);
rp-=tmp.first*(last-i+1);
rm-=tmp.second*(last-i+1);
}
mp[x]=MP(rp,rm);
return MP(rp,rm);
}
int main()
{
int T,i,j;
scanf("%d",&T);
phi[1]=sp[1]=mu[1]=sm[1]=1;
for(i=2;i<=m;i++)
{
if(!np[i]) pri[++num]=i,phi[i]=i-1,mu[i]=-1;
sp[i]=sp[i-1]+phi[i],sm[i]=sm[i-1]+mu[i];
for(j=1;j<=num&&i*pri[j]<=m;j++)
{
np[i*pri[j]]=1;
if(i%pri[j]==0)
{
phi[i*pri[j]]=phi[i]*pri[j];
mu[i*pri[j]]=0;
break;
}
mu[i*pri[j]]=-mu[i];
phi[i*pri[j]]=phi[i]*(pri[j]-1);
}
}
while(T--)
{
ll a;
scanf("%lld",&a);
pll tmp=dfs(a);
printf("%lld %lld\n",tmp.first,tmp.second);
}
return 0;
}【BZOJ3944/4805】Sum/歐拉函數求和 杜教篩