【BZOJ4173】數學

Description

Input

輸入文件的第一行輸入兩個正整數 。

Output

如題

Sample Input

Sample Output

HINT

N,M<=10^15

題解：STEP 1：

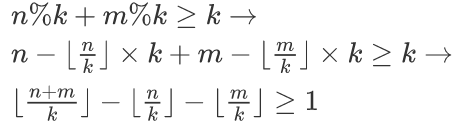
這步還是很容易的吧~畢竟原來的式子不太舒服。但是註意，最後一個式子的取值只能為0或1，所以就變成了。

STEP 2：

這步倒是難理解一些，但是考慮：我們將這三個等式都算出來，如果滿足了左邊那個條件，那麽這三個等式加起來為1，對答案的貢獻正好為$\varphi(k)$。否則，因為左邊的式子不是0就是1，那麽只能是0，這三個等式加起來對答案的貢獻也就是0。

STEP 3：這三個式子長得差不多，我們只考慮一個

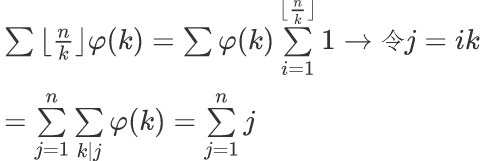
這步就顯得比較套路了。我們強行給那個底式賦予實際意義，然後就轉化成了簡單的歐拉函數性質應用。三個式子都算完後，你發現結果正好是nm。那麽最終的答案就是$\varphi(n)\varphi(m)nm$

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
typedef long long ll;
const ll mod=998244353;
typedef long long ll;
ll n,m;
ll phi(ll x)
{
	ll ret=x,i;
	for(i=2;i*i<=x;i++)
	{
		if(x%i==0)
		{
			ret=ret/i*(i-1);
			while(x%i==0)	x/=i;
		}
	}
	if(x!=1)	ret=ret/x*(x-1);
	return ret%mod;
}
int main()
{
	scanf("%lld%lld",&n,&m);
	printf("%lld",phi(n)*phi(m)%mod*(n%mod)%mod*(m%mod)%mod);
	return 0;
}

【BZOJ4173】數學 歐拉函數神題