POJ 2286 The Rotation Game(IDA*)
阿新 • • 發佈:2017-06-14
symbols lock several 代碼 time list sym stat strong The Rotation Game
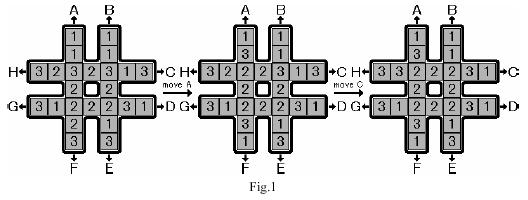
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.
| Time Limit: 15000MS | Memory Limit: 150000K | |
| Total Submissions: 6396 | Accepted: 2153 |
Description
The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind.
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration.
Input
The input consists of no more than 30 test cases. Each test case has only one line that contains 24 numbers, which are the symbols of the blocks in the initial configuration. The rows of blocks are listed from top to bottom. For each row the blocks are listed from left to right. The numbers are separated by spaces. For example, the first test case in the sample input corresponds to the initial configuration in Fig.1. There are no blank lines between cases. There is a line containing a single `0‘ after the last test case that ends the input.Output
For each test case, you must output two lines. The first line contains all the moves needed to reach the final configuration. Each move is a letter, ranging from `A‘ to `H‘, and there should not be any spaces between the letters in the line. If no moves are needed, output `No moves needed‘ instead. In the second line, you must output the symbol of the blocks in the center square after these moves. If there are several possible solutions, you must output the one that uses the least number of moves. If there is still more than one possible solution, you must output the solution that is smallest in dictionary order for the letters of the moves. There is no need to output blank lines between cases.Sample Input
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 0
Sample Output
AC 2 DDHH 2
題目鏈接:POJ 2286
第一道IDA*題目,由於用的是遞歸的寫法,代碼量實際上不會很大,只要在dfs入口處做好各種判斷就可以了 ,能用IDA*的前提至少答案要存在,如果不存在的話搜索深度會無限加深就沒有意義了,然後每一次都用估價函數剪枝即可,再加一個防止來回的剪枝速度可以快一倍
大致偽代碼如下:
void dfs(state, dep)
{
計算此時狀態下的估價函數值h(state)
if(h(state)==0)
已到終點,返回true
else if(h(state)+dep>Maxdep)
在規定的Maxdep內一定走不到終點,返回false
else
{
for....
{
得到新狀態n_state
if(dfs(n_state,dep))
return 1;
}
}
return 0;
}
代碼:
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <sstream>
#include <numeric>
#include <cstring>
#include <bitset>
#include <string>
#include <deque>
#include <stack>
#include <cmath>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int, int> pii;
typedef long long LL;
const double PI = acos(-1.0);
const int N = 25;
int arr[N], cnt[4];
int Max_dep, Num;
char ans[1000];
int top,Back[8]={5,4,7,6,1,0,3,2};//Back數組,減掉正拉動後又馬上反向拉動的無意義搜索
int pos[8][7] =
{
{1, 3, 7, 12, 16, 21, 23}, //A0
{2, 4, 9, 13, 18, 22, 24}, //B1
{11, 10, 9, 8, 7, 6, 5}, //C2
{20, 19, 18, 17, 16, 15, 14}, //D3
{24, 22, 18, 13, 9, 4, 2},//E4
{23, 21, 16, 12, 7, 3, 1},//F5
{14, 15, 16, 17, 18, 19, 20},//G6
{5, 6, 7, 8, 9, 10, 11},//H7
};
int Need(int cur[])
{
int i;
cnt[1] = cnt[2] = cnt[3] = 0;
for (i = 7; i <= 9; ++i)
++cnt[cur[i]];
for (i = 12; i <= 13; ++i)
++cnt[cur[i]];
for (i = 16; i <= 18; ++i)
++cnt[cur[i]];
int Need_1 = 8 - cnt[1], Need_2 = 8 - cnt[2], Need_3 = 8 - cnt[3];
int Min_Need = min(Need_1, min(Need_2, Need_3));
return Min_Need;
}
int IDA_star(int dep, int Arr[],int pre)
{
int Need_cur = Need(Arr);
if (Need_cur == 0)
{
Num = Arr[7];
return 1;
}
if (Need_cur + dep > Max_dep)
return 0;
int Temp_arr[N];
for (int Opsid = 0; Opsid < 8; ++Opsid)
{
if(Opsid==pre)
continue;
ans[top++] = ‘A‘ + Opsid;
for (int i = 1; i <= 24; ++i)
Temp_arr[i] = Arr[i];
for (int i = 0; i < 7; ++i)
Temp_arr[pos[Opsid][i]] = Arr[pos[Opsid][(i + 1) % 7]];
if (IDA_star(dep + 1, Temp_arr, Back[Opsid]))
return 1;
else
--top;
}
return 0;
}
int main(void)
{
while (~scanf("%d", &arr[1]) && arr[1])
{
for (int i = 2; i <= 24; ++i)
scanf("%d", &arr[i]);
if (Need(arr) == 0)
{
puts("No moves needed");
printf("%d\n", arr[7]);
}
else
{
top = 0;
Max_dep = 1;
Num = -1;
while (!IDA_star(0, arr, -1))
++Max_dep;
ans[top] = ‘\0‘;
puts(ans);
printf("%d\n", Num);
}
}
return 0;
}
POJ 2286 The Rotation Game(IDA*)
