邊賦以權值的圖稱為網或帶權圖，帶權圖的生成樹也是帶權的，生成樹T各邊的權值總和稱為該樹的權。

最小生成樹（MST）：權值最小的生成樹。

生成樹和最小生成樹的應用：要連通n個城市需要n－1條邊線路。可以把邊上的權值解釋為線路的造價。則最小生成樹表示使其造價最小的生成樹。

構造網的最小生成樹必須解決下面兩個問題：

1、盡可能選取權值小的邊，但不能構成回路；

2、選取n－1條恰當的邊以連通n個頂點；

MST性質：假設G＝(V,E)是一個連通網，U是頂點V的一個非空子集。若(u,v)是一條具有最小權值的邊，其中u∈U，v∈V－U，則必存在一棵包含邊(u,v)的最小生成樹。

1.prim算法

基本思想：假設G＝(V，E)是連通的，TE是G上最小生成樹中邊的集合。算法從U＝{u0}（u0∈V）、TE＝{}開始。重復執行下列操作：

在所有u∈U，v∈V－U的邊(u，v)∈E中找一條權值最小的邊(u0,v0)並入集合TE中，同時v0並入U，直到V＝U為止。

此時，TE中必有n-1條邊，T=(V，TE)為G的最小生成樹。

Prim算法的核心:始終保持TE中的邊集構成一棵生成樹。

註意：prim算法適合稠密圖，其時間復雜度為O(n^2)，其時間復雜度與邊得數目無關。

看了上面一大段文字是不是感覺有點暈啊，為了更好理解我在這裏舉一個例子，示例如下：

（1）圖中有6個頂點v1-v6，每條邊的邊權值都在圖上；在進行prim算法時，我先隨意選擇一個頂點作為起始點，當然我們一般選擇v1作為起始點，好，現在我們設U集合為當前所找到最小生成樹裏面的頂點，TE集合為所找到的邊，現在狀態如下：

U={v1}； TE={}；

（2）現在查找一個頂點在U集合中，另一個頂點在V-U集合中的最小權值，如下圖，在紅線相交的線上找最小值。

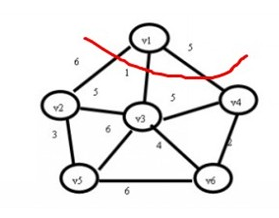
通過圖中我們可以看到邊v1-v3的權值最小為1，那麽將v3加入到U集合，（v1，v3）加入到TE，狀態如下：

U={v1，v3}； TE={（v1，v3）}；

（3）繼續尋找，現在狀態為U={v1，v3}； TE={（v1，v3）}；在與紅線相交的邊上查找最小值。

我們可以找到最小的權值為（v3，v6）=4，那麽我們將v6加入到U集合，並將最小邊加入到TE集合，那麽加入後狀態如下：

U={v1，v3，v6}； TE={（v1，v3），（v3，v6）}； 如此循環一下直到找到所有頂點為止。

（4）下圖像我們展示了全部的查找過程：

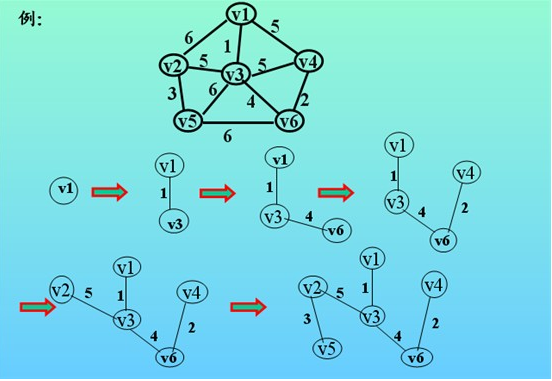
克魯斯卡爾（Kruskal）算法（只與邊相關）

算法描述：克魯斯卡爾算法需要對圖的邊進行訪問，所以克魯斯卡爾算法的時間復雜度只和邊又關系，可以證明其時間復雜度為O（eloge）。

算法過程：

1.將圖各邊按照權值進行排序

2.將圖遍歷一次，找出權值最小的邊，（條件：此次找出的邊不能和已加入最小生成樹集合的邊構成環），若符合條件，則加入最小生成樹的集合中。不符合條件則繼續遍歷圖，尋找下一個最小權值的邊。

3.遞歸重復步驟1，直到找出n-1條邊為止（設圖有n個結點，則最小生成樹的邊數應為n-1條），算法結束。得到的就是此圖的最小生成樹。

克魯斯卡爾（Kruskal）算法因為只與邊相關，則適合求稀疏圖的最小生成樹。而prime算法因為只與頂點有關，所以適合求稠密圖的最小生成樹。

而kruskal算法的時間復雜度為O(eloge)跟邊的數目有關，適合稀疏圖。

算法描述：克魯斯卡爾算法需要對圖的邊進行訪問，所以克魯斯卡爾算法的時間復雜度只和邊又關系，可以證明其時間復雜度為O（ElogE）。

算法過程：

1.將圖各邊按照權值進行排序

2.將圖遍歷一次，找出權值最小的邊，（條件：此次找出的邊不能和已加入最小生成樹集合的邊構成環），若符合條件，則加入最小生成樹的集合中。不符合條件則繼續遍歷圖，尋找下一個最小權值的邊。

3.遞歸重復步驟1，直到找出n-1條邊為止（設圖有n個結點，則最小生成樹的邊數應為n-1條），算法結束。得到的就是此圖的最小生成樹。判斷是否構成環：《算法導論》提供的一種方法是采用一種"不相交集合數據結構"，也就是並查集了。核心內容就是如果某兩個節點屬於同一棵樹，那麽將它們合並後一定會形成回路。

克魯斯卡爾（Kruskal）算法因為只與邊相關，則適合求稀疏圖的最小生成樹。而prime算法因為只與頂點有關，所以適合求稠密圖的最小生成樹。

無向帶權圖的最小生成樹算法——Prim及Kruskal算法思路