prim演算法基礎詳解(無向賦權圖的最小生成樹MST)
帶權圖分為有向和無向,無向圖的最短路徑又叫做最小生成樹,有prime演算法和kruskal演算法
生成樹的概念:聯通圖G的一個子圖如果是一棵包含G的所有頂點的樹,則該子圖稱為G的生成樹 生成樹是聯通圖的極小連通子圖。
所謂極小是指:若在樹中任意增加一條邊,則將出現一個迴路;若去掉一條邊,將會使之變成非連通圖。生成樹各邊的權值總和稱為生成樹的權。
權最小的生成樹稱為最小生成樹,常用的演算法有prime演算法和kruskal演算法。這裡僅介紹prime演算法..
演算法描述如下:
1.將所有的結點分成兩個集合。一部分是在最小生成樹中的點(記為集合A),另一部分是不在最小生成樹中的點(即待加入的點,記為集合B)。
2.開始的時候取任意一個點v作為頂點加入最小生成樹中(A),然後遍歷集合B,選取一個點vj使得(v,vj)的權值最小,然後將vj加入A集合,B集合中刪去vj(刪去操作可以用一個intree[i]陣列來進行操作)
3.重複2步驟直到所有點遍歷完畢。
注意:這裡說的重複步驟2是指每次找的與頂點v的邊權值最小的結點!
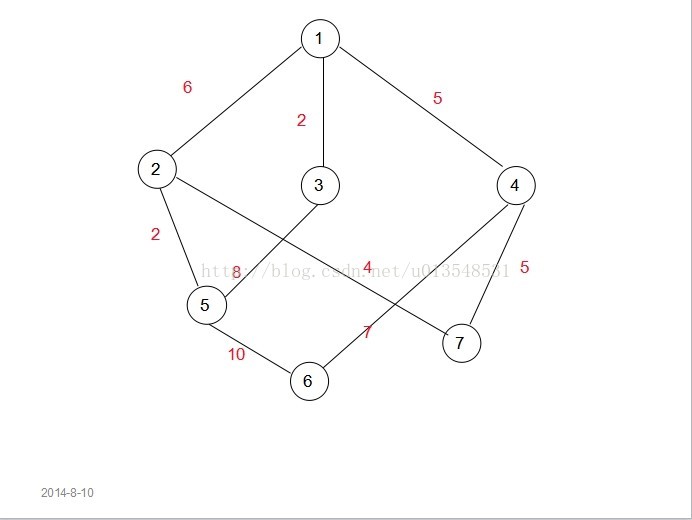
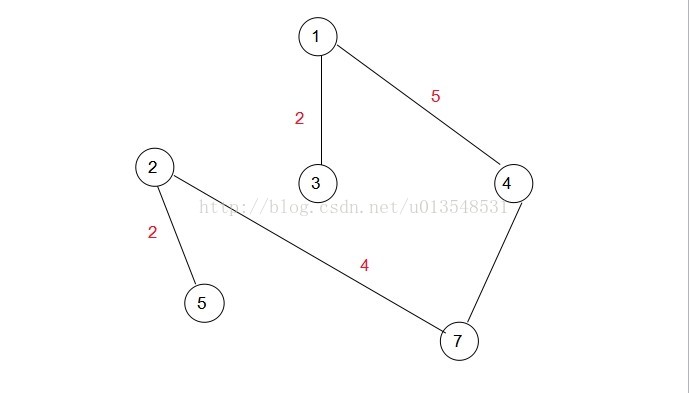
結合例子來看一下。(如下圖)
選擇1為初始結點,intree[1]標記為1.
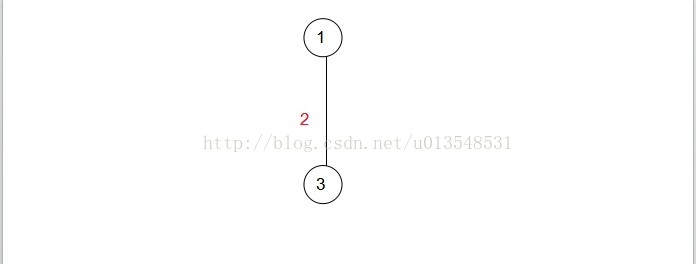
遍歷剩下的6個結點,找到(1,vj)中weight最小的那一個,顯然是3,讓3加入集合A,即intree[3]標記為1
然後注意此時集合A中有了兩個元素(結點1和結點3)開始的時候我認為是從3開始遍歷找3與其他點的最小權值,但是再次注意我們每次只找與頂點(這裡就1結點)邊權值最小的點。
3結點入隊後,1就可以與5結點間接相連了,所以每次在A中加入一個結點,都要更新頂結點與其他結點的關聯與否以及權值。
這一點非常重要是演算法的重要步驟。
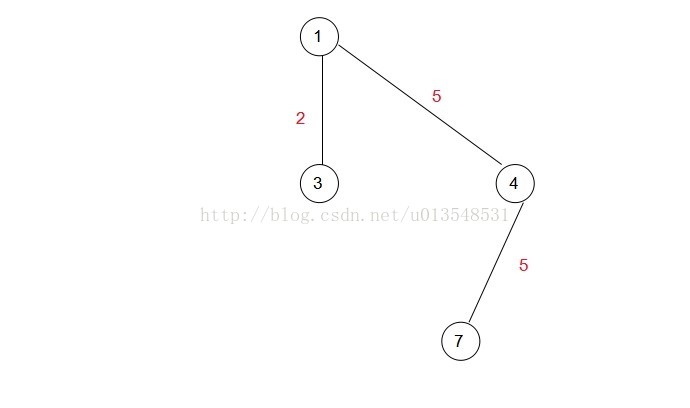
正如此時(1,5) = 8 (1,4) = 5 (1,2) = 6 ,顯然下一次應該加入A集合的是點4,所以:
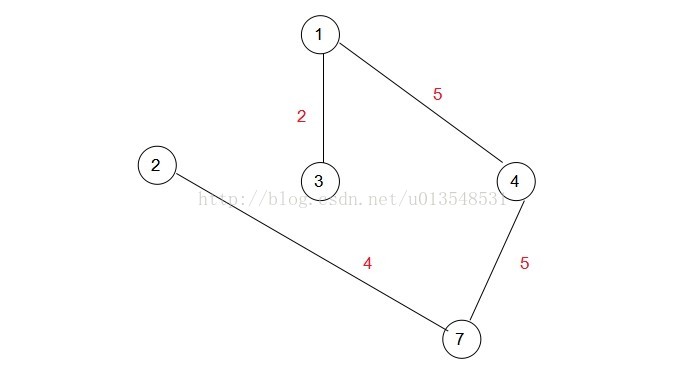
接下來就是:
附上程式碼及測試樣例。
#include <stdio.h> #include <string.h> #define maxn 10 #define INF 100000 int node; int G[maxn + 1][maxn + 1];/*構建的圖,必須是一個無向連通賦權圖,G[i][j]存取權值*/ int intree[maxn];/*結點i在最小生成樹中*/ int minweight[maxn];/*到i點的最小權重*/ int sumweight; void initialize() { memset(intree,0,sizeof(intree)); memset(minweight,0,sizeof(minweight)); for(int i = 0 ; i <= maxn ; i++) for(int j = 0 ; j <= maxn ; j++) G[i][j] = INF; sumweight = 0; } void prime(int n) { int node,Minweight; for(int i = 1 ; i <= n ; i++) minweight[i] = G[1][i]; /*先把1結點放進最小生成樹,那麼要知道1到其餘結點的最小權重*/ intree[1] = 1;/*1點進入集合A,最小生成樹集*/ for(int i = 2 ; i <= n ; i++) /*一共n個點,已經把1加入最小生成樹,那麼還剩下n-1個點*/ { Minweight = INF; for(int j = 1 ; j <= n ; j++) { if(minweight[j] < Minweight && !intree[j]) { Minweight = minweight[j]; node = j; } } printf("選擇的結點標號為:%d\n",node); intree[node] = 1; sumweight += Minweight; /*每次在A中加入新的點,更新頂結點到各節點的權重*/ for(int j = 1 ; j <= n ; j++) if(!intree[j] && minweight[j] > G[node][j]) /*更新B集合*/ minweight[j] = G[node][j]; } } int main() { int Node,Edge; int vertex1,vertex2,weight; initialize(); scanf("%d%d",&Node,&Edge); for(int i = 1 ; i <= Edge ; i++) { scanf("%d%d%d",&vertex1,&vertex2,&weight); G[vertex1][vertex2] = weight; G[vertex2][vertex1] = weight; } prime(Node); printf("%d\n",sumweight); return 0; } /* 7 9 1 2 6 1 3 2 1 4 5 2 5 2 2 7 4 3 5 8 4 6 7 4 7 5 5 6 10 答案是25 */