基於K-means Clustering聚類算法對電商商戶進行級別劃分(含Octave仿真)
阿新 • • 發佈:2017-07-05
fprintf highlight 初始 load ogre max init 金額 定時
在從事電商做頻道運營時,每到關鍵時間節點,大促前,季度末等等,我們要做的一件事情就是品牌池打分,更新所有店鋪的等級。例如,所以的商戶分入SKA,KA,普通店鋪,新店鋪這4個級別,對於不同級別的商戶,會給予不同程度的流量扶持或廣告策略。通常來講,在一定時間段內,評估的維度可以有:UV,收訂金額,好評率,銷退金額,廣告位點擊率,轉化率,pc端流量、手機端流量、客單價......等n多個維度,那麽如何在這n多個維度中找到一種算法,來將我們的品牌劃分到4個級別中呢?今天所討論的K-means聚類算法是其中一種,基於某電商頻道296個品牌的周銷量真實數據,我們來進行品牌池劃分。
首先, K-means聚類算法可以描述為如下幾步:
1、隨機選取K個質心(centroids);
2、計算每個數據點距離K個質心的距離,選擇距離最小的一個質心作為該數據點的所屬組。例如,某數據點距離#3質心最近,那麽它就屬於#3組。
3、更新質心的坐標,將每個組的數據點坐標相加求平均值,得出新的質心位置並更新。
4、重復第二和第三步n次。
其中,K和n是提前指定的。
為了將K-means運行過程可視化,我們只取296的品牌的2個維度:UV與收訂金額。主控代碼如下:
%% ================= Part 1: load data ==================== fprintf(‘load parameters.\n\n‘); pkg load io; tmp = xlsread(‘data.xlsx‘); id=tmp(:,1); X=tmp(:,2:3); %% =================== Part 2: set parameters ====================== K = 4; max_iters = 10; %% =================== Part 3: K-Means Clustering ====================== fprintf(‘\nRunning K-Means clustering on example dataset.\n\n‘); initial_centroids = kMeansInitCentroids(X,K); % Run K-Means algorithm. The ‘true‘ at the end tells our function to plot % the progress of K-Means [centroids, idx] = runkMeans(X, initial_centroids, max_iters, true); fprintf(‘\nK-Means Done.\n\n‘);
K-Means Clustering Algorithm核心代碼:
function [centroids, idx] = runkMeans(X, initial_centroids, ...
max_iters, plot_progress)
[m n] = size(X);
K = size(initial_centroids, 1);
centroids = initial_centroids;
previous_centroids = centroids;
idx = zeros(m, 1);
% Run K-Means
for i=1:max_iters
% Output progress
fprintf(‘K-Means iteration %d/%d...\n‘, i, max_iters);
if exist(‘OCTAVE_VERSION‘)
fflush(stdout);
end
% For each example in X, assign it to the closest centroid
idx = findClosestCentroids(X, centroids);
% Given the memberships, compute new centroids
centroids = computeCentroids(X, idx, K);
end
end
選擇最近質心的算法:
function idx = findClosestCentroids(X, centroids)
K = size(centroids, 1);
idx = zeros(size(X,1), 1);
m = size(X,1);
for(i = 1:m)
distance = -1;
index = -1;
for(j=1:K)
e = X(i,:)-centroids(j,:);
d_tmp = e*e‘;
if(distance == -1)
distance = d_tmp;
index = j;
else
if (d_tmp<distance)
distance = d_tmp;
index = j;
endif
endif
endfor
idx(i) = index;
endfor
end
重新計算質心及初始化質心的算法:
function centroids = computeCentroids(X, idx, K) [m n] = size(X); centroids = zeros(K, n); num = zeros(K,1); for(i = 1:m) c = idx(i,:); centroids(c,:) += X(i,:); num(c,:)++; endfor centroids = centroids./num; function centroids = kMeansInitCentroids(X, K) centroids = zeros(K, size(X, 2)); randidx = randperm(size(X, 1)); centroids = X(randidx(1:K), :); end
經過十次叠代後,分組的結果如下:
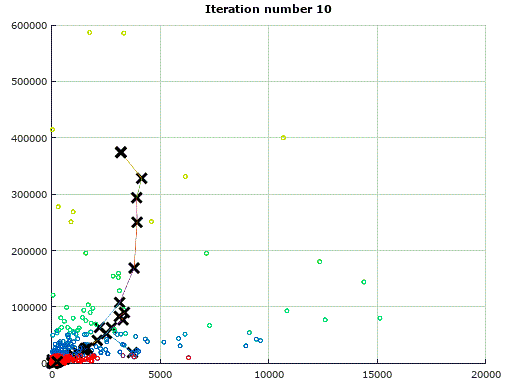
在我本地的原始數據表格中,共有約20個維度來衡量每個店鋪的運行情況,根據K-means聚類算法可以很輕松的將它們歸類,雖然無法將其進行可視化操作,但原理與二維K-means完全相同。
基於K-means Clustering聚類算法對電商商戶進行級別劃分(含Octave仿真)
