●贅述題目

對於一個長為n（n<50000）的序列（序列中的數小於1000000000），現有如下兩種指令：

Q a b c：詢問區間[a,b]中第c小的數。

C p b：將序列中的從左往右數第p個數改成b。

●題解

（整體二分應該可以做吧。。。但寫不來了）

主席樹+樹狀數組套線段樹維護。

本題和POJ 2104 K-th Number相比，多了一個修改操作，但真的做得我心累。

看看POJ 2104 的查詢函數：

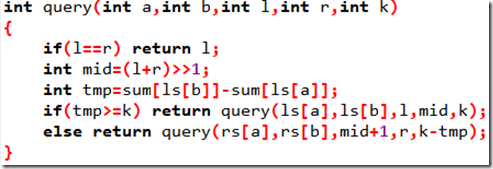
查詢區間到底是往左還是往右，這決於tmp與k大小關系。但本題因為有修改操作，導致上圖的sum[ ]存的信息不正確，無法正確二分下去。所以我們需要就修改操作進行信息的更新。

對於一個修改操作C p b，我們可以發現，這個操作會影響tr[p-n]這一堆主席樹，那當然是不能直接枚舉這一堆主席樹

於是便嘗試再另外弄一個東西來單獨維護修改後的信息。

不難發現，這一堆主席樹，它們的修改操作是一模一樣的，那便可以看作是一個區間修改，單點查詢（如下圖）呢，那我們就用樹狀數組來維護。

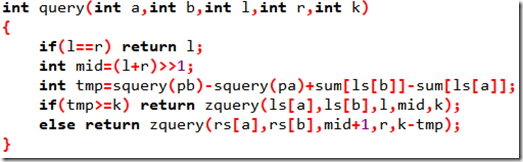
squery(x)是對樹狀數組的詢問，表示序列區間[1-x]內有多少在[l-r]（權值）範圍內的數發生了變化(少了則減，多了則加)。

舉個例子，當原序列為 1 2 3 4 ，已經執行了修改操作C 2 5

若 l=1，r=4：squery(1)=0; squery(2)=-1; squery(3)=-1; squery(4)=-1;

若 l=5，r=8 : squery(1)=0; squery(2)=1; squery(3)=1; squery(4)=1;

若 l=1，r=8 : squery(1)=0; squery(2)=0; squery(3)=0; squery(4)=0;

（一定要弄懂哦。）

另外，樹狀數組該如何維護在[l-r]範圍內的數發生的變化呢，那就樹套樹唄（以前從未寫過樹套樹。。。），對於每個樹狀數組的節點建一顆權值線段樹。

○至此，便有了一個大致的修改操作的思路：

對於C p b ，

先是枚舉樹狀數組的節點（數組數組區間修改（單點查詢），不用多說了吧）

for(int i=p;i<=n;i+=lowbit(i)) xmodify( ) ，對枚舉到的節點裏套的權值線段樹進行單點修改。

到時候查詢樹狀數組的時候，就for(int i=p;i>0;i-=lowbit(i)) ret+=xquery( )

（註意：若每個樹狀數組節點裏都套的是一棵完整的權值線段樹，空間必然不夠，但因為修改數不超過10000，每次修改都只修改log n條鏈，這意味著我們需要用到的權值線段樹的某些位置，在修改時臨時建就好了，最後每個樹狀數組節點裏都套的都是我們想象的完整的權值線段樹，實際上只是幾條鏈，甚至一條鏈沒有。）

那麽，完了嗎？

我們算一算： m個操作，每個操作有一個log級別的主席樹查詢，再有一個 log級別的樹狀數組查詢， 再套一個log級別的權值線段樹查詢，總的是復雜度是mlogloglog，可能要超時呢。

看看別的大佬的做法，每次主席樹查詢到[l-r]區間時，我們查詢的每個權值線段樹區間也是[l-r]（且該區間是直接二分得到的，而不是幾個小區間拼湊而來），那便可以先用一個數組存下要用的權值線段樹的節點，當詢問樹狀數組時由儲存的權值線段樹的節點直接獲取權值區間信息便是了。這樣是一個 mloglog的復雜度。

所以，這裏生長著兩棵樹，一顆是主席樹（保存初始信息），一顆是套了線段樹的樹狀數組（維護修改信息）。那麽，本題也就結束了。

好吧，其實還有漫長的調試查錯呢！

●代碼

先大致解釋一下函數名：（XX表示原函數名，如build,modify,squery。。。）

zXX表示關於主席樹的函數；

sXX表示關於樹狀數組的函數；

xXX表示關於線段樹的函數；

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm> 
const int MAXN = 60010;
const int M = 2500010;
using namespace std;
int sum[M],ls[M],rs[M];
int xx[MAXN],aa[MAXN],tr[MAXN],s[MAXN],use[MAXN];
int tot=0,cnt,n,m,pa,pb;
struct operation{
	char ch;int a,b,c;
}op[10005];
int discrete(int x){return lower_bound(xx+1,xx+cnt+1,x)-xx;}
void xmodify(int &u,int l,int r,int x,int d)
{
	if(!u) u=++tot,sum[u]=0;
	sum[u]+=d;
	if(l==r){return;}
	int mid=(l+r)>>1;
	if(x<=mid) xmodify(ls[u],l,mid,x,d);
	else xmodify(rs[u],mid+1,r,x,d);
}
int lowbit(int x) {return x&-x;}
void smodify(int p,int x,int d) 
{
	for(int i=p;i<=n;i+=lowbit(i)) xmodify(s[i],1,cnt,x,d);
} 
int squery(int x)
{
	int ret=0;
	for(int i=x;i>0;i-=lowbit(i)) ret+=sum[ls[use[i]]];
	return ret;
}
void zbuild(int &u,int l,int r)
{
	u=++tot; sum[u]=0;
	if(l==r) return;
	int mid=(l+r)>>1;
	zbuild(ls[u],l,mid);
	zbuild(rs[u],mid+1,r); 
}
void zupdate(int &u,int last,int l,int r,int p)
{
	u=++tot; sum[u]=sum[last]+1;
	if(l==r) return;
	ls[u]=ls[last]; rs[u]=rs[last]; 
	int mid=(l+r)>>1;
	if(p<=mid) zupdate(ls[u],ls[last],l,mid,p);
	else zupdate(rs[u],rs[last],mid+1,r,p);
}
int zquery(int a,int b,int l,int r,int k)
{
	if(l==r) return l;
	int mid=(l+r)>>1;
	int tmp=squery(pb)-squery(pa)+sum[ls[b]]-sum[ls[a]];
	if(tmp>=k) 
	{
		for(int i=pa;i>0;i-=lowbit(i)) use[i]=ls[use[i]];
		for(int i=pb;i>0;i-=lowbit(i)) use[i]=ls[use[i]];
		return zquery(ls[a],ls[b],l,mid,k);	
	}
	else 
	{
		for(int i=pa;i>0;i-=lowbit(i)) use[i]=rs[use[i]];
		for(int i=pb;i>0;i-=lowbit(i)) use[i]=rs[use[i]];
		return zquery(rs[a],rs[b],mid+1,r,k-tmp);
	}
}
int main()
{
	int ans,dd,T;
	scanf("%d",&T);
	while(T--)
	{
		tot=cnt=dd=0;
		scanf("%d%d",&n,&m);
		memset(s,0,sizeof(s));
		memset(ls,0,sizeof(ls));
		memset(rs,0,sizeof(rs));
		for(int i=1;i<=n;i++) scanf("%d",&aa[i]),xx[++dd]=aa[i];
		for(int i=1;i<=m;i++)
		{
			scanf(" %c",&op[i].ch);
			if(op[i].ch==‘Q‘) scanf("%d%d%d",&op[i].a,&op[i].b,&op[i].c);
			else scanf("%d%d",&op[i].a,&op[i].b),xx[++dd]=op[i].b;
		}
		sort(xx+1,xx+dd+1);
		cnt=unique(xx+1,xx+dd+1)-xx-1;
		zbuild(tr[0],1,cnt);
		for(int i=1;i<=n;i++)
		{
			int p=discrete(aa[i]);
			zupdate(tr[i],tr[i-1],1,cnt,p);
		}
		for(int i=1,a,b,k;i<=m;i++)
		{
			a=op[i].a; b=op[i].b;
			if(op[i].ch==‘Q‘)
			{
				k=op[i].c;
				pa=a-1; pb=b;
				for(int j=pa;j>0;j-=lowbit(j)) use[j]=s[j];
				for(int j=pb;j>0;j-=lowbit(j)) use[j]=s[j];
				ans=zquery(tr[a-1],tr[b],1,cnt,k); 
				printf("%d\n",xx[ans]);
			}
			else 
			{
				int x=discrete(aa[a]),y=discrete(b);
				smodify(a,x,-1); smodify(a,y,1);
				aa[a]=b;
			}
		}		
	}
	return 0;
}

●ZOJ 2112 Dynamic Rankings