漢諾塔算法之求解最佳步數
寫的不好,但是請尊重版權,轉載請註明出處: http://www.cnblogs.com/xiaovw/
何為漢諾塔?
答:漢諾塔是根據一個傳說形成的一個問題。漢諾塔(又稱河內塔)問題是源於印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子,在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。並且規定,在小圓盤上不能放大圓盤,在三根柱子之間一次只能移動一個圓盤。
關於漢諾塔的經典問題:
有三根相鄰的柱子,標號為A,B,C,A柱子上從下到上按金字塔狀疊放著n個不同大小的圓盤,要把所有盤子一個一個移動到柱子B上,並且每次移動同一根柱子上都不能出現大盤子在小盤子上方,請問至少需要多少次移動。轉載請註明出處: http://www.cnblogs.com/xiaovw/
題目要求:
1.在小圓盤上不能放大圓盤。
2.在三根柱子之間一回只能移動一個圓盤。
3.只能移動在最頂端的圓盤。
算法分析:
在這裏我們暫且只討論到達制定目標所需的步數,不討論移動的步驟。
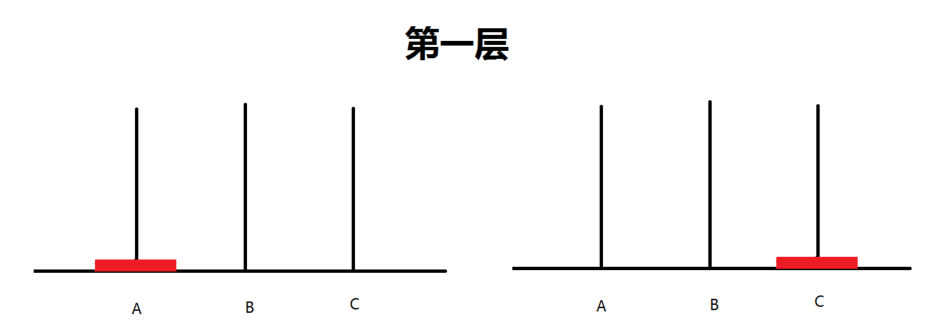
當只有一層的時候,只需一步便可從A到C:A -> C
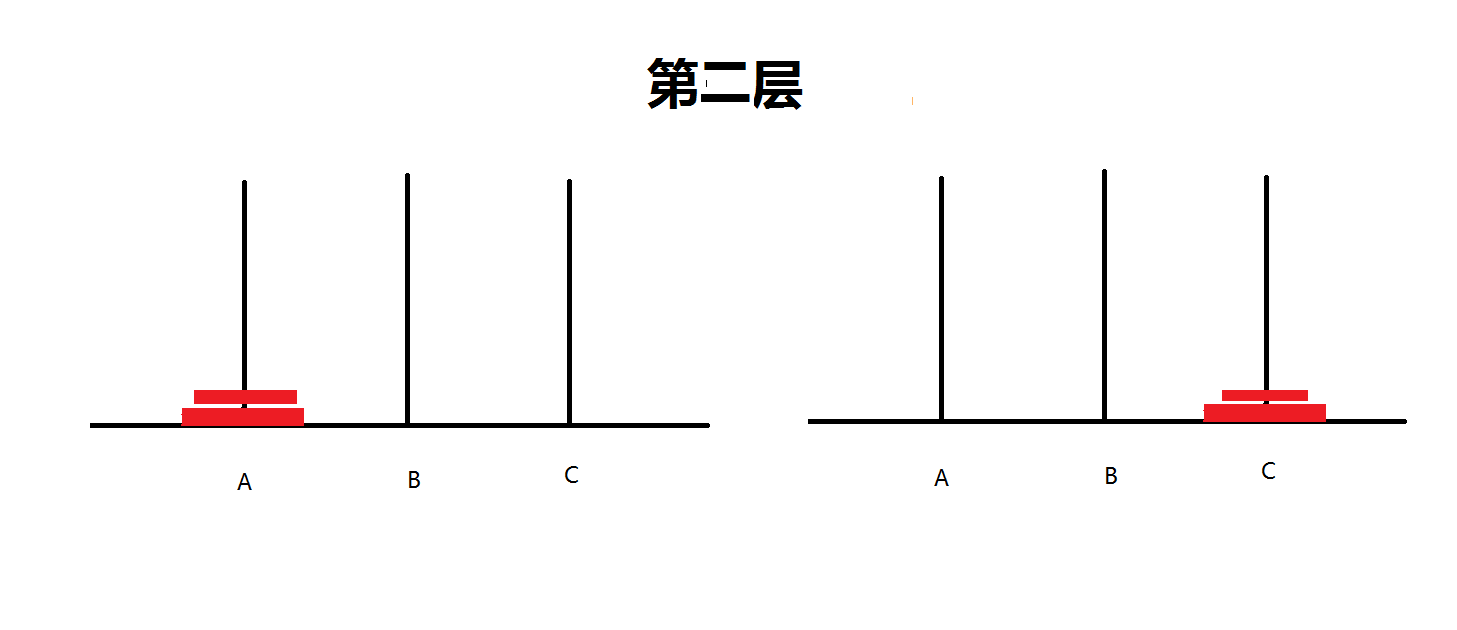
第二層將所有的盤子從A移動到C 有3種選擇(不做演示,可在此鏈接內自行進行測試,http://www.4399.com/flash/49864_4.htm)
第三層 有7種選擇
第四層 有15種選擇
第五層 有31種選擇
。。。。
由此測試數據:
f( 1 ) = 1;
f( 2 ) = 3 ;
f( 3 ) = 7;
f( 4 ) = 15;
f( 5 ) = 31;
.......
可發現: f(n)= 2 * f(n-1)+ 1; (註意:測試f(1)時,f(0)=0)
即:f(n)= 2^n - 1;
/* f(n)= 2 * f(n-1)+ 1不驗證,當64層時,數據長度太長*/
1class Hannuota{ 2 public static void main(){ 3 4 Scanner sc= new Scanner(System.in); 5 int n=sc.nextInt;6 System.out.println("走了"+Math.pow(2,n)-1+"步"); 7 } 8 }
轉載請註明出處: http://www.cnblogs.com/xiaovw/
漢諾塔算法之求解最佳步數
