【智能算法】粒子群尋優算法
1.理論基礎
粒子群算法（particle swarm optimization，PSO）是計算智能領域中的一種生物啟發式方法，屬於群體智能優化算法的一種，常見的群體智能優化算法主要有如下幾類：
（1）蟻群算法（Ant Colony Optimization，簡稱ACO）[1992年提出]；
（2）粒子群優化算法（Particle Swarm Optimization，簡稱PSO）[1995年提出]（簡單易於實現，也是目前應用最為廣泛的群體智能優化算法）；
（3）菌群優化算法（Bacterial Foraging Optimization，簡稱BFO）[2002年提出]；
（4）蛙跳算法（Shuffled Frog Leading Algorithm，簡稱SFLA）[2003年提出]；
（5）人工蜂群算法（Artificial Bee Colony Algorithm，簡稱ABC）[2005年提出]；
除了上述幾種常見的群體智能算法以外，還有一些並不是廣泛應用的群體智能算法，比如螢火蟲算法、布谷鳥算法、蝙蝠算法以及磷蝦群算法等等。
而其中的粒子群優化算法（PSO）源於對鳥類捕食行為的研究，鳥類捕食時，找到食物最簡單有限的策略就是搜尋當前距離食物最近的鳥的周圍。
舉個通俗的例子：
一群鳥在尋找食物，在這個區域內有一個食物，所有的鳥都不知道食物在哪裏，但食物發出了香味，鳥通過香味的濃烈能判斷出自己的當前位置距離食物有多遠，同時鳥群之間是可以交流並告知離食物最近的鳥的位置的。試想一下這個時候會發生什麽？
鳥甲：哈哈哈，原來我離食物最近！
鳥乙、丙、丁…:我得趕緊往鳥甲那裏過去看看！
同時各自鳥在位置不停變化的時候，離食物的距離也不斷的變化，所以一定有過離食物最近的位置，這是他們的一個參考。
鳥某某：我剛才的位置好像離食物很近了，我得往那裏再靠近點！
通過這樣一個過程，不斷的變化，最終鳥群會向食物方向聚集，達到目標。在這個變化的過程中，影響鳥的運動狀態變化的有兩個因素：
- 離食物最近的鳥的位置
- 自己之前達到過的離食物最近的位置
而鳥的每次的位置變化，除了考慮以上的兩個因素還有一個因素就是慣性。而對位置的變化，通過變化量（速度）來表示。
通過以上的例子，我們可以把鳥抽象為沒有質量和體積的微粒(點)，並延伸到N維空間，粒子I 在N維空間的位置表示為矢量Xi＝(x1，x2，…，xN)，飛行速度表示為矢量Vi＝(v1，v2，…，vN)．每個粒子都有一個由目標函數決定的適應值(fitness value)，並且知道自己到目前為止發現的最好位置(pbest)和現在的位置Xi．這個可以看作是粒子自己的飛行經驗．除此之外，每個粒子還知道到目前為止整個群體中所有粒子發現的最好位置(gbest)(gbest是pbest中的最好值)．這個可以看作是粒子同伴的經驗．粒子就是通過自己的經驗和同伴中最好的經驗來決定下一步的運動。歸結為下面的兩個公式：
(公式-1）
（公式-2）
其中，為慣性權重因子，（什麽是權重因子，這個後面會講到，此處大概知道有這麽一個參數即可）；d=1,2，…，D；i=1,2，…，n；k為當前叠代次數；Vid為粒子的速度；c1和c2是非負的常數，稱為加速因子；r1和r2是分布於[0,1]區間的隨機數。為了防止粒子的滿目搜索，一般建議限制位置和速度在一定的區間。
2.粒子群尋優算法的案例與實現
假設有如下非線性函數，需要在一定範圍內找出最大值和最大值的位置，本文用Python實現。
（公式-3）
我們先通過python把上面函數使用matplotlib把它畫處理，讓我們有個直觀的感受。
# -*- coding: utf-8 -*- from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np fig = plt.figure() ax = Axes3D(fig) X = np.arange(-2, 2, 0.05) Y = np.arange(-2, 2, 0.05) X, Y = np.meshgrid(X, Y) Z = np.sin(np.sqrt(X**2+Y**2))/np.sqrt(X**2+Y**2)+np.exp((np.cos(2*np.pi*X)+np.cos(2*np.pi*Y))/2)-2.71289 ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=‘hot‘) plt.show()
此處使用mpl_toolkits.mplot3d畫3D圖，在代碼中，分別使用numpy中的arange創建等差長度為0.05的數據點向量，區間為[-2,2]之間，然後使用meshgrid將向量轉換給對應的矩陣，這樣的話，後面的函數式中就可以使用np中的三角函數和數學函數了，如果不這樣的話，還得一個一個點的根據公式去做循環，拼接Z的向量點。
運行出來的圖如下：
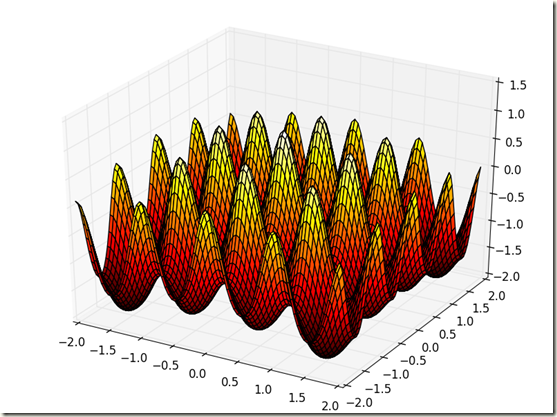
從函數圖形中可以看出，這個函數有很多的局部極大值，而真正的極限位置就是在（0,0），極大值為1.005。下面就通過粒子群算法來找尋這個極大值和極大值的位置。根據粒子群算法函數求極值的算法流程如下圖所示：
在pycham作為python的IDE中，建立一個名為PSO.py的文件，文件中編寫一個名PSO的類。
2.1 參數的設定
設置慣性參數為常數1，也就是公式-1中的為常數1；設置加速度因子為非負的兩個常數，公式-1的中的c1和c2；設置叠代次數為300；設置粒子群的規模為20；為了防止粒子的盲目搜索，將位置和速度限制在區間[-2,2]、[-0.5,0.5]；
具體代碼如下：
def __init__(self): self.w = self.getweight() self.lr = self.getlearningrate() self.maxgen = self.getmaxgen() self.sizepop = self.getsizepop() self.rangepop = self.getrangepop() self.rangespeed = self.getrangespeed() def getweight(self): # 慣性權重 weight = 1 return weight def getlearningrate(self): # 分別是粒子的個體和社會的學習因子，也稱為加速常數 lr = (0.49445,1.49445) return lr def getmaxgen(self): # 最大叠代次數 maxgen = 300 return maxgen def getsizepop(self): # 種群規模 sizepop = 20 return sizepop def getrangepop(self): # 粒子的位置的範圍限制,x、y方向的限制相同 rangepop = (-2,2) return rangepop def getrangespeed(self): # 粒子的速度範圍限制 rangespeed = (-0.5,0.5) return rangespeed
2.2 種群初始化
隨機初始化粒子位置和粒子的速度，並根據適應度函數計算粒子適應度值，我們的適應度函數就是公式-3這個函數。
首先定義一個適應度函數
def func(self,x): # x輸入粒子位置 # y 粒子適應度值 if (x[0]==0)&(x[1]==0): y = np.exp((np.cos(2*np.pi*x[0])+np.cos(2*np.pi*x[1]))/2)-2.71289 else: y = np.sin(np.sqrt(x[0]**2+x[1]**2))/np.sqrt(x[0]**2+x[1]**2)+np.exp((np.cos(2*np.pi*x[0])+np.cos(2*np.pi*x[1]))/2)-2.71289 return y
然後初始化粒子和計算適應度值
def initpopvfit(self,sizepop): pop = np.zeros((sizepop,2)) v = np.zeros((sizepop,2)) fitness = np.zeros(sizepop) for i in range(sizepop): pop[i] = [(np.random.rand()-0.5)*self.rangepop[0]*2,(np.random.rand()-0.5)*self.rangepop[1]*2] v[i] = [(np.random.rand()-0.5)*self.rangepop[0]*2,(np.random.rand()-0.5)*self.rangepop[1]*2] fitness[i] = self.func(pop[i]) return pop,v,fitness
2.3 尋找初始化後的極值
def getinitbest(self,fitness,pop): # 群體最優的粒子位置及其適應度值 gbestpop,gbestfitness = pop[fitness.argmax()].copy(),fitness.max() #個體最優的粒子位置及其適應度值,使用copy()使得對pop的改變不影響pbestpop，pbestfitness類似 pbestpop,pbestfitness = pop.copy(),fitness.copy() return gbestpop,gbestfitness,pbestpop,pbestfitness
此處需要分別找到群體極值和個體粒子的極值。
2.4 叠代尋優
通過循環叠代，不斷的更新粒子的位置和速度，根據新粒子的適應度值更新個體和群體的極值。這部分的代碼如下：
def run(self): pop, v, fitness = self.initpopvfit(self.sizepop) gbestpop, gbestfitness, pbestpop, pbestfitness = self.getinitbest(fitness, pop) result = np.zeros(self.maxgen) for i in range(self.maxgen): # 速度更新 for j in range(self.sizepop): v[j] += self.lr[0] * np.random.rand() * (pbestpop[j] - pop[j]) + self.lr[1] * np.random.rand() * ( gbestpop - pop[j]) v[v < self.rangespeed[0]] = self.rangespeed[0] v[v > self.rangespeed[1]] = self.rangespeed[1] # 粒子位置更新 for j in range(self.sizepop): pop[j] += 0.5 * v[j] pop[pop < self.rangepop[0]] = self.rangepop[0] pop[pop > self.rangepop[1]] = self.rangepop[1] # 適應度更新 for j in range(self.sizepop): fitness[j] = self.func(pop[j]) for j in range(self.sizepop): if fitness[j] > pbestfitness[j]: pbestfitness[j] = fitness[j] pbestpop[j] = pop[j].copy() if pbestfitness.max() > gbestfitness: gbestfitness = pbestfitness.max() gbestpop = pop[pbestfitness.argmax()].copy() result[i] = gbestfitness return result
2.4 結果分析
通過在主函數文件中，實例化PSO類，調用run這個函數，運行上面的代碼
from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np from PSO import * pso = PSO() result = pso.run() plt.figure() plt.plot(result) plt.show()
當叠代了300次之後，畫出每代最優個體適應度值的曲線，結果如下：
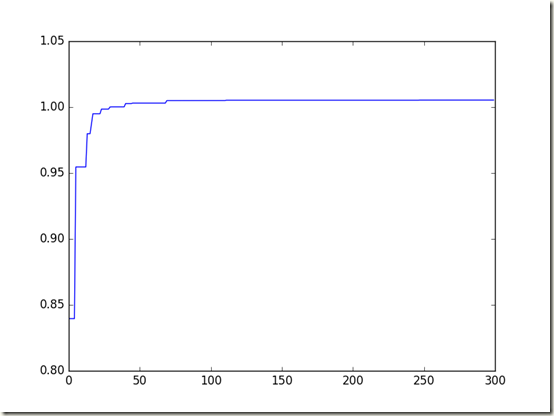
最終得到的最優個體適應度值為：1.00538866933，對應的粒子位置為：[ 2.37513360e-05 3.41265823e-04]，通過比較，PSO算法能得到最優值，接近函數實際的最優值1.005。
通過以上，證明PSO算法具有較強的函數極值尋優能力。
3.延伸與算法改進
講到這裏，我們再來回顧一下之前粒子更新速度（公式-1）中的這個慣性權重因子，所謂慣性權重因子，體現的是粒子繼承上一次叠代速度的能力。較大的一個慣性權重因子有利於全局的搜索，而一個小的慣性權重因子則更加利於局部的搜索。為了更好的平衡算法的全局搜索與局部搜索的能力，常給慣性權重因子改為隨叠代次數變化的一個函數，一般常用的慣性權重因子函數有以下幾種：
（公式-4）
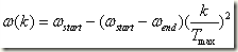（公式-5）
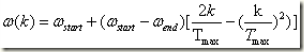（公式-6）
（公式-7）
這幾種的變化圖如下：
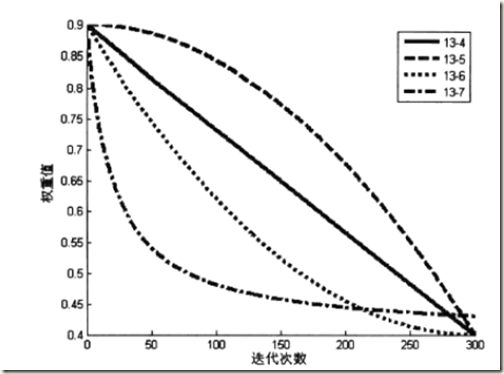
從變化圖中，可以看到（公式-5）中，前期變化較慢，取值較大，維持了算法的全局搜索能力；後期
變化較快，極大的提高了算法的局部尋優能力，通過這種
權重的變化函數，可以取得比
固定不變的那種情況要好的效果。
【智能算法】粒子群尋優算法