題意：給一個圖，求一棵生成樹滿足點$s$的度數$\leq d_s$且點$t$的度數$\leq d_t$

我們觀察一下樣例

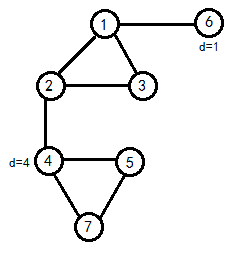
如果我們把與$s,t$相連的邊刪掉

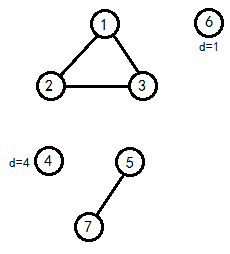
可以看出，$(1,2,3)$與$s,t$都有邊相連，而$(5,7)$只與$t$有邊相連

我們只需分別求出每塊的任意一棵生成樹，然後連接$6$和$(1,2,3)$，連接$(1,2,3)$和$4$，連接$4$和$(5,7)$即可

於是我們有這樣的算法：對於被分割出來的每一塊求出任意一棵生成樹，最後把它們通過$s$和$t$連起來

分割出來的塊有兩種：第一種只與$s$或$t$相連，這種塊必須連接到對應的$s$或$t$

第二種與$s$和$t$都相連，這種塊中只有一個塊能同時連接$s$和$t$，其他的只能連接$s,t$中的某一個，對於這種塊我們貪心地連接即可

註意特判是否有一條邊連接$s$和$t$，如果有，並且沒有第二種塊，則這條邊一定要連，否則一定不連

不難，但是算是鍛煉代碼能力的題吧我太弱了

  1 #include<stdio.h>
  2 struct edgex{
  3     int x,y;
  4 }ex[400010],ans[200010];
  5 struct edge{
  6     int to,nex;
  7 }e[800010];
  8 int h[200010],col[200010],fa[200010],n,tot,s,t,ds,dt,cnt,cstp;
  9 bool st[200010],v[200010],done[200010
 
],cst,mpst;
 10 void add(int a,int b){
 11     tot++;
 12     e[tot].to=b;
 13     e[tot].nex=h[a];
 14     h[a]=tot;
 15 }
 16 void dfs1(int f,int x){
 17     col[x]=f;
 18     v[x]=1;
 19     for(int i=h[x];i;i=e[i].nex){
 20         if(e[i].to!=t&&e[i].to!=s&&col[e[i].to]==0
 
)dfs1(f,e[i].to);
 21     }
 22 }
 23 void dfs2(int f,int x){
 24     col[x]=f;
 25     for(int i=h[x];i;i=e[i].nex){
 26         if(e[i].to!=t&&e[i].to!=s&&col[e[i].to]==0)dfs2(f,e[i].to);
 27     }
 28 }
 29 void calc(int x){
 30     done[x]=1;
 31     fa[x]=s;
 32     for(int i=h[x];i;i=e[i].nex){
 33         if(fa[e[i].to]!=s){
 34             cnt++;
 35             ans[cnt].x=x;
 36             ans[cnt].y=e[i].to;
 37             calc(e[i].to);
 38         }
 39     }
 40 }
 41 int getfa(int x){
 42     return(x==fa[x])?x:fa[x]=getfa(fa[x]);
 43 }
 44 int main(){
 45     int m,i,a;
 46     scanf("%d%d",&n,&m);
 47     for(i=1;i<=m;i++)scanf("%d%d",&ex[i].x,&ex[i].y);
 48     scanf("%d%d%d%d",&s,&t,&ds,&dt);
 49     for(i=1;i<=m;i++){
 50         if((ex[i].x==s&&ex[i].y==t)||(ex[i].x==t&&ex[i].y==s)){
 51             cstp=i;
 52             cst=1;
 53             break;
 54         }
 55     }
 56     for(i=1;i<=m;i++){
 57         if(i!=cstp){
 58             add(ex[i].x,ex[i].y);
 59             add(ex[i].y,ex[i].x);
 60         }
 61     }
 62     for(i=h[s];i;i=e[i].nex){
 63         if(col[e[i].to]==0)dfs1(e[i].to,e[i].to);
 64     }
 65     for(i=h[t];i;i=e[i].nex){
 66         if(col[e[i].to]==0)
 67             dfs2(e[i].to,e[i].to);
 68         else if(v[e[i].to]){
 69             st[col[e[i].to]]=1;
 70             mpst=1;
 71         }
 72     }
 73     for(i=1;i<=n;i++)fa[i]=i;
 74     fa[t]=s;
 75     for(i=h[s];i;i=e[i].nex){
 76         if(!st[col[e[i].to]]&&!done[e[i].to]){
 77             cnt++;
 78             ans[cnt].x=s;
 79             ans[cnt].y=e[i].to;
 80             ds--;
 81             calc(e[i].to);
 82         }
 83     }
 84     for(i=h[t];i;i=e[i].nex){
 85         if(!st[col[e[i].to]]&&!done[e[i].to]){
 86             cnt++;
 87             ans[cnt].x=t;
 88             ans[cnt].y=e[i].to;
 89             dt--;
 90             calc(e[i].to);
 91         }
 92     }
 93     if(cst&&!mpst){
 94         cnt++;
 95         ans[cnt].x=s;
 96         ans[cnt].y=t;
 97         ds--;
 98         dt--;
 99     }else{
100         for(i=h[t];i;i=e[i].nex){
101             if(st[col[e[i].to]]){
102                 cnt++;
103                 ans[cnt].x=s;
104                 ans[cnt].y=col[e[i].to];
105                 ds--;
106                 cnt++;
107                 ans[cnt].x=t;
108                 ans[cnt].y=e[i].to;
109                 dt--;
110                 calc(col[e[i].to]);
111                 break;
112             }
113         }
114     }
115     if(dt<0||ds<0){
116         puts("No");
117         return 0;
118     }
119     i=h[s];
120     while(i&&ds>0){
121         a=getfa(e[i].to);
122         if(a!=s){
123             fa[a]=s;
124             cnt++;
125             ans[cnt].x=s;
126             ans[cnt].y=e[i].to;
127             ds--;
128             calc(e[i].to);
129         }
130         i=e[i].nex;
131     }
132     i=h[t];
133     while(i&&dt>0){
134         a=getfa(e[i].to);
135         if(a!=s){
136             fa[a]=s;
137             cnt++;
138             ans[cnt].x=t;
139             ans[cnt].y=e[i].to;
140             dt--;
141             calc(e[i].to);
142         }
143         i=e[i].nex;
144     }
145     for(i=1;i<=n;i++)getfa(i);
146     for(i=1;i<=n;i++){
147         if(fa[i]!=s){
148             puts("No");
149             return 0;
150         }
151     }
152     puts("Yes");
153     for(i=1;i<n;i++)printf("%d %d\n",ans[i].x,ans[i].y);
154 }

[CF723F] st-Spanning Tree