P1244 青蛙過河

題目描述

有一條河，左邊一個石墩(A區)上有編號為1，2，3，4，…，n的n只青蛙，河中有k個荷葉(C區)，還有h個石墩(D區)，右邊有一個石墩(B區)，如下圖所示。n只青蛙要過河(從左岸石墩A到右岸石墩B)，規則為：

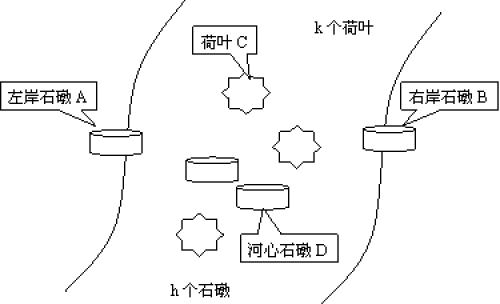
(1)石墩上可以承受任意多只青蛙，荷葉只能承受一只青蛙(不論大小)；

(2)青蛙可以：A→B(表示可以從A跳到B，下同)，A→C，A→D，C→B，D→B，D→C，C→D；

(3)當一個石墩上有多只青蛙時，則上面的青蛙只能跳到比它大1號的青蛙上面。

你的任務是對於給出的h，k，計算並輸出最多能有多少只青蛙可以根據以上規則順利過河?

輸入輸出格式

輸入格式：

兩個整數h,k

輸出格式：

一個整數，表示最多能有多少只青蛙可以根據以上規則順利過河。

輸入輸出樣例

2 3

16

分析：

情況一：

當k確定而h=0時,沒有中間柱子,蛤蛤們只能通過荷葉來移動.每片荷葉只能有1位青蛙.所以要求最大的通過數目就必須把所有的荷葉用上.

由於他們必須按順序從小到大從上到下壘起來（跳到石墩B上面的時候）.所以這種情況下,最大通過數目為k+1.

就是石墩B上面跳一只，其余每片荷葉上面跳一只。

因為題目要求中青蛙可以直接到B。

(2)青蛙可以：A→B(表示可以從A跳到B，下同)，A→C，A→D，C→B，D→B，D→C，C→D；

情況二：

當k確定而h=1時,有一個中間柱子s1。

先將1->k+1號（1k+1個）放在s1石墩上，然後將k+2->2k+2號（1k+1個）放到全部荷葉和石墩B上。

情況三：

當k確定而h=2時,有兩個中間柱子s1，s2。

先將1->2k+2號（2k+2個）放在s1石墩上，然後將2k+3->3k+3號（1k+1個）放在s2石墩上，

然後再將3k+4->4k+4（1k+1個）放到全部荷葉和石墩B上。

既然如此我們用 f[h][k] 表示 h 個石墩 k 片荷葉時最多的青蛙數

顯然 f[0][k]=k+1

h=1時，讓盡可能多的青蛙跳到D區石墩上（f[0][k]），再讓盡可能多的青蛙跳到B石墩上（f[0][k]），最後讓D區石墩上的青蛙跳到B上，所以 f[1][k]= f[0][k] + f[0][k]。

h=2時，讓盡可能多的青蛙跳到D區的第一個石墩上（f[1][k]），再讓盡可能多的青蛙跳到D區的第二個石墩上（f[0][k]），再讓盡可能多的青蛙跳到B石墩上（f[0][k]），再讓D區第二個石墩上的青蛙跳到B石墩上，最後讓D區第一個石墩上的青蛙跳到B上，所以 f[2][k]=f[1][k]+ f[0][k] + f[0][k]。

以此類推。f[h][k]=f[h-1][k]+f[h-2][k]+…+f[1][k]+f[0][k]+f[0][k]

由於青蛙跳到D區石墩上和從D區跳到B上環境是一樣的（即空石墩的數量是一樣的），所以不用擔心青蛙跳不到B上啦。

得到遞推公式之後，讓我們再來看一看。

f[1][k]= f[0][k] + f[0][k]=2*(k+1)

f[2][k]=f[1][k]+ f[0][k] + f[0][k] =f[1][k]+f[1][k]=2*2*(k+1)

f[3][k]=f[2][k]+ f[1][k]+ f[0][k] + f[0][k]=f[2][k]+f[2][k]=2*2*2*(k+1)

… f[h][k]=2*f[h-1][k]=(2^h)*(k+1)

於是我們得到了通項公式f[h][k] =(2^h)*(k+1)

1 #include<iostream>
2 #include<math.h>
3 using namespace std;
4 int main()
5 {
6     int i,j,m,h,k,a;
7     while(cin>>h>>k)
8     cout<<(k+1)*pow(2,h)<<endl;
9 }

P1244 青蛙過河