P1244 青蛙過河

• • 362通過
  • 525提交
• 題目提供者該用戶不存在
• 標簽
• 難度普及-
• 時空限制1s / 128MB

提交 討論 題解

最新討論更多討論

• 題目什麽意思
• 題目看不懂啊

題目描述

有一條河，左邊一個石墩(A區)上有編號為1，2，3，4，…，n的n只青蛙，河中有k個荷葉(C區)，還有h個石墩(D區)，右邊有一個石墩(B區)，如下圖所示。n只青蛙要過河(從左岸石墩A到右岸石墩B)，規則為：

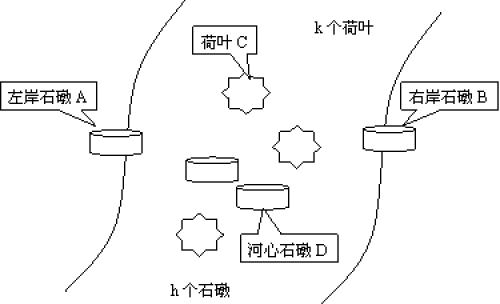
(1)石墩上可以承受任意多只青蛙，荷葉只能承受一只青蛙(不論大小)；

(2)青蛙可以：A→B(表示可以從A跳到B，下同)，A→C，A→D，C→B，D→B，D→C，C→D；

(3)當一個石墩上有多只青蛙時，則上面的青蛙只能跳到比它大1號的青蛙上面。

你的任務是對於給出的h，k，計算並輸出最多能有多少只青蛙可以根據以上規則順利過河?

輸入輸出格式

兩個整數h,k

一個整數，表示最多能有多少只青蛙可以根據以上規則順利過河。

輸入輸出樣例

2 3

16
分析：這道題很顯然是一道遞推的題，和漢諾塔問題差不多，影響答案的是荷葉的數量和石墩的數量，那麽我們設f[i][j]表示有i個石墩,j個荷葉，最多能跳過去多少只青蛙.先從小的情況來考慮，f[0][j] = j + 1,很顯然，先讓一只青蛙跳到石墩上，然後其它青蛙跳到荷葉上，最後統一跳到石墩上.那麽f[1][j]呢？有了另外一個石墩，我們可以先讓盡量多的小號青蛙跳到D上，再讓盡量多的大號青蛙跳到B上，最後讓D上的青蛙跳到B上，這樣我們可以先把B當作不存在，那麽就是前一種情況f[0][j],然後把D當作不存在，還是前一種情況f[0][j],那麽f[1][j]就是2*f[0][j].
      再來分析一下f[2][j],跳到B上的和跳到一號石墩的青蛙數是2*f[0][j],跳到二號石墩的青蛙數就是f[1][j]了，因為我們只考慮二號石墩，忽略一號石墩，把二號石墩當作了終點,那麽相當於只有一號石墩的這種情況，其他石墩就不能當作終點了。可以得到f[i][j] = sum{f[k][j]} + f[0][k](0 <= k < j),f[0][j]告訴了，那麽我們可以化簡這個式子，f[1][j] = 2*f[0][j],f[2][j] = 4*f[0][j],f[3][j] = 8*f[0][j],那麽最終答案就是（k+1）*2^h.
      比較值得回味的幾個地方：1.定義狀態看哪些量對答案有影響，最直接的就是把輸入定義為狀態.2.先分析小情況，一步一步推向一般情況.
 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

int h,k;

int main()
{
    scanf("%d%d",&h,&k);
    printf("%d\n",(k + 1) * (1 << h));
    
    return 0;
}

洛谷P1244 青蛙過河