題目鏈接：http://hihocoder.com/problemset/problem/1048

題目大意：用1*2或者2*1的方塊鋪滿一個N*M的大方格，共有多少種方法。結果對1e9+7取余。2<=N<=1000, 3<=m<=5

解題思路：挑戰程序設計競賽上有基本上一樣的題目，可以參考，原題中也有提示。大致思路就是，如果從左往右鋪的話，那麽對第i行j列的方塊來說，第i-1行的方塊一定全部鋪過，第j+2行的一定沒有鋪過。所以我們可以保存第i行和第i+1行的狀態，然後遞推。又由於m<=5，所以可以將兩行的狀態壓縮成整數。具體遞推過程：

 1 int t = 0;                                                                
 
 2 //位置(i, j)已經被鋪                                                     
 3 if(s1 & (1 << k)){                                                        
 4     if(j < m) t = dp[i][j + 1][s1][s2];            //由下一個方塊遞推         
 5     else if(i < n) t = dp[i + 1][1][s2][0];        //從下一行第一個遞推     
 

 6     else t = 0;                                                            
 7 }                                                                        
 8 else{                                                                    
 9     if(j < m && !(s1 & (1 << (k - 1))))         //
 
可以橫著鋪             
10         t += dp[i][j][s1 | (1 << k - 1) | (1 << k)][s2];                
11     t %= mod;                                                            
12     if(i < n && !(s2 & (1 << k)))                 //可以豎著鋪             
13         t += dp[i][j][s1 | (1 << k)][s2 | (1 << k)];                    
14     t %= mod;                                                            
15 }                                                                        
16 dp[i][j][s1][s2] += t % mod;                                            

完整代碼：

 1 const int maxn = 1e3 + 5;
 2 int n, m;
 3 int dp[maxn][6][35][35];
 4 
 5 void solve(){
 6     memset(dp, 0, sizeof(dp)); 
 7     for(int s2 = (1 << m) - 1; s2 >= 0; s2--) dp[n][m][(1 << m) - 1][s2] = 1;
 8     for(int i = n; i >= 1; i--){
 9         for(int j = m; j >= 1; j--){
10             int k = m - j;
11             for(int s1 = (1 << m) - 1; s1 >= 0; s1--){
12                 for(int s2 = (1 << m) - 1; s2 >= 0; s2--){
13                     int t = 0;                                                                
14                     //位置(i, j)已經被鋪                                                     
15                     if(s1 & (1 << k)){                                                            
16                         if(j < m) t = dp[i][j + 1][s1][s2];            //由下一個方塊遞推         
17                         else if(i < n) t = dp[i + 1][1][s2][0];        //從下一行第一個遞推     
18                         else t = 0;                                                            
19                     }                                                                        
20                     else{                                                                    
21                         if(j < m && !(s1 & (1 << (k - 1))))         //可以橫著鋪             
22                             t += dp[i][j][s1 | (1 << k - 1) | (1 << k)][s2];                
23                         t %= mod;                                                            
24                         if(i < n && !(s2 & (1 << k)))                 //可以豎著鋪             
25                             t += dp[i][j][s1 | (1 << k)][s2 | (1 << k)];                    
26                         t %= mod;                                                            
27                     }                                                                        
28                     dp[i][j][s1][s2] += t % mod;                                            
29                 }
30             }
31         }
32     }
33     printf("%d\n", dp[1][1][0][0]);
34 }
35 int main(){
36     scanf("%d %d", &n, &m);
37     solve();
38 }

題目：

#1048 : 狀態壓縮·二

描述

歷經千辛萬苦，小Hi和小Ho終於到達了舉辦美食節的城市！雖然人山人海，但小Hi和小Ho仍然抑制不住興奮之情，他們放下行李便投入到了美食節的活動當中。美食節的各個攤位上各自有著非常多的有意思的小遊戲，其中一個便是這樣子的：

小Hi和小Ho領到了一個大小為N*M的長方形盤子，他們可以用這個盒子來裝一些大小為2*1的蛋糕。但是根據要求，他們一定要將這個盤子裝的滿滿的，一點縫隙也不能留下來，才能夠將這些蛋糕帶走。

這麽簡單的問題自然難不倒小Hi和小Ho，於是他們很快的就拿著蛋糕離開了~

但小Ho卻不只滿足於此，於是他提出了一個問題——他們有多少種方案來裝滿這個N*M的盤子呢？

值得註意的是，這個長方形盤子的上下左右是有區別的，如在N=4, M=3的時候，下面的兩種方案被視為不同的兩種方案哦！

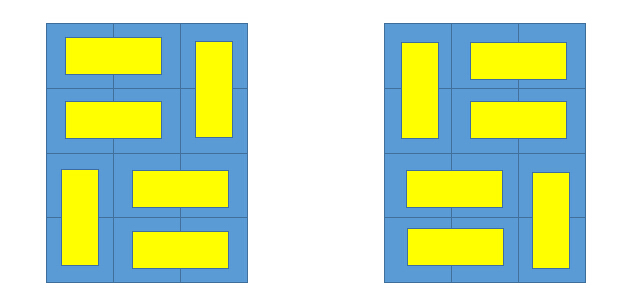
提示：我們來玩拼圖吧！不過不同的枚舉方式會導致不同的結果哦！

輸入

每個測試點（輸入文件）有且僅有一組測試數據。

每組測試數據的第一行為兩個正整數N、M，表示小Hi和小Ho拿到的盤子的大小。

對於100%的數據，滿足2<=N<=1000, 3<=m<=5。<>

輸出

考慮到總的方案數可能非常大，只需要輸出方案數除以1000000007的余數。

樣例輸入

2 4

樣例輸出

5

hihoCoder 1048 : 狀態壓縮·二