noip 2015 day1
T1 神奇的幻方
題目描述
幻方是一種很神奇的N*N矩陣:它由數字1,2,3,……,N*N構成,且每行、每列及兩條對角線上的數字之和都相同。
當N為奇數時,我們可以通過以下方法構建一個幻方:
首先將1寫在第一行的中間。
之後,按如下方式從小到大依次填寫每個數K(K=2,3,…,N*N):
1.若(K−1)在第一行但不在最後一列,則將K填在最後一行,(K−1)所在列的右一列;
2.若(K−1)在最後一列但不在第一行,則將K填在第一列,(K−1)所在行的上一行;
3.若(K−1)在第一行最後一列,則將K填在(K−1)的正下方;
4.若(K−1)既不在第一行,也不在最後一列,如果(K−1)的右上方還未填數,則將K填在(K−1)的右上方,否則將K填在(K−1)的正下方。
現給定N請按上述方法構造N*N的幻方。
輸入輸出格式
輸入格式:
輸入文件只有一行,包含一個整數N即幻方的大小。
輸出格式:
輸出文件包含N行,每行N個整數,即按上述方法構造出的N*N的幻方。相鄰兩個整數之間用單個空格隔開。
輸入輸出樣例
輸入樣例#1:3輸出樣例#1:
8 1 6 3 5 7 4 9 2輸入樣例#2:
25
327 354 381 408 435 462 489 516 543 570 597 624 1 28 55 82 109 136 163 190 217 244 271 298 325 353 380 407 434 461 488 515 542 569 596 623 25 27 54 81 108 135 162 189 216 243 270 297 324 326 379 406 433 460 487 514 541 568 595 622 24 26 53 80 107 134 161 188 215 242 269 296 323 350 352 405 432 459 486 513 540 567 594 621 23 50 52 79 106 133 160 187 214 241 268 295 322 349 351 378 431 458 485 512 539 566 593 620 22 49 51 78 105 132 159 186 213 240 267 294 321 348 375 377 404 457 484 511 538 565 592 619 21 48 75 77 104 131 158 185 212 239 266 293 320 347 374 376 403 430 483 510 537 564 591 618 20 47 74 76 103 130 157 184 211 238 265 292 319 346 373 400 402 429 456 509 536 563 590 617 19 46 73 100 102 129 156 183 210 237 264 291 318 345 372 399 401 428 455 482 535 562 589 616 18 45 72 99 101 128 155 182 209 236 263 290 317 344 371 398 425 427 454 481 508 561 588 615 17 44 71 98 125 127 154 181 208 235 262 289 316 343 370 397 424 426 453 480 507 534 587 614 16 43 70 97 124 126 153 180 207 234 261 288 315 342 369 396 423 450 452 479 506 533 560 613 15 42 69 96 123 150 152 179 206 233 260 287 314 341 368 395 422 449 451 478 505 532 559 586 14 41 68 95 122 149 151 178 205 232 259 286 313 340 367 394 421 448 475 477 504 531 558 585 612 40 67 94 121 148 175 177 204 231 258 285 312 339 366 393 420 447 474 476 503 530 557 584 611 13 66 93 120 147 174 176 203 230 257 284 311 338 365 392 419 446 473 500 502 529 556 583 610 12 39 92 119 146 173 200 202 229 256 283 310 337 364 391 418 445 472 499 501 528 555 582 609 11 38 65 118 145 172 199 201 228 255 282 309 336 363 390 417 444 471 498 525 527 554 581 608 10 37 64 91 144 171 198 225 227 254 281 308 335 362 389 416 443 470 497 524 526 553 580 607 9 36 63 90 117 170 197 224 226 253 280 307 334 361 388 415 442 469 496 523 550 552 579 606 8 35 62 89 116 143 196 223 250 252 279 306 333 360 387 414 441 468 495 522 549 551 578 605 7 34 61 88 115 142 169 222 249 251 278 305 332 359 386 413 440 467 494 521 548 575 577 604 6 33 60 87 114 141 168 195 248 275 277 304 331 358 385 412 439 466 493 520 547 574 576 603 5 32 59 86 113 140 167 194 221 274 276 303 330 357 384 411 438 465 492 519 546 573 600 602 4 31 58 85 112 139 166 193 220 247 300 302 329 356 383 410 437 464 491 518 545 572 599 601 3 30 57 84 111 138 165 192 219 246 273 301 328 355 382 409 436 463 490 517 544 571 598 625 2 29 56 83 110 137 164 191 218 245 272 299
說明
對於100%的數據,1<=N<=39且N為奇數。
NOIp2015 提高組 d1t1

#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #define N 100 using namespace std; int n,b[N][N]; bool vis[N][N]; struct A { int x,y; }a[N]; int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } int main() { n=read(); a[1].x=1;a[1].y=n/2+1;vis[a[1].x][a[1].y]=true;b[a[1].x][a[1].y]=1; for(int i=2;i<=n*n;i++) { if(a[i-1].x==1&&a[i-1].y!=n) {a[i].x=n,a[i].y=a[i-1].y+1; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true; continue;} if(a[i-1].x!=1&&a[i-1].y==n) {a[i].y=1,a[i].x=a[i-1].x-1; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true; continue;} if(a[i-1].x==1&&a[i-1].y==n) {a[i].x=a[i-1].x+1,a[i].y=a[i-1].y; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true; continue;} if(a[i-1].x!=1&&a[i-1].y!=n) { if(!vis[a[i-1].x-1][a[i-1].y+1]&&a[i-1].x-1>=1&&a[i-1].x-1<=n&&a[i-1].y+1>1&&a[i-1].y+1<=n) {a[i].x=a[i-1].x-1,a[i].y=a[i-1].y+1; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true;} else {a[i].x=a[i-1].x+1,a[i].y=a[i-1].y; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true;} continue; } } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) printf("%d ",b[i][j]); printf("\n"); } return 0; }莫名RE 70
mdzz忘記自己還開了個結構體這個事情了、、、
O(≧口≦)O zz 啊!!! 結構體下標為這個數,而數最大要到40*40,因此會RE

#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> #include<algorithm> #define N 1600 using namespace std; int n,b[N][N]; bool vis[N][N]; struct A { int x,y; }a[N]; int read() { int x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } int main() { n=read(); a[1].x=1;a[1].y=n/2+1;vis[a[1].x][a[1].y]=true;b[a[1].x][a[1].y]=1; for(int i=2;i<=n*n;i++) { if(a[i-1].x==1&&a[i-1].y!=n) {a[i].x=n,a[i].y=a[i-1].y+1; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true; continue;} if(a[i-1].x!=1&&a[i-1].y==n) {a[i].y=1,a[i].x=a[i-1].x-1; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true; continue;} if(a[i-1].x==1&&a[i-1].y==n) {a[i].x=a[i-1].x+1,a[i].y=a[i-1].y; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true; continue;} if(a[i-1].x!=1&&a[i-1].y!=n) { if(!vis[a[i-1].x-1][a[i-1].y+1]&&a[i-1].x-1>=1&&a[i-1].x-1<=n&&a[i-1].y+1>1&&a[i-1].y+1<=n) {a[i].x=a[i-1].x-1,a[i].y=a[i-1].y+1; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true;} else {a[i].x=a[i-1].x+1,a[i].y=a[i-1].y; b[a[i].x][a[i].y]=i; vis[a[i].x][a[i].y]=true;} continue; } } for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) printf("%d ",b[i][j]); printf("\n"); } return 0; }AC代碼
T2 信息傳遞
題目描述
有n個同學(編號為1到n)正在玩一個信息傳遞的遊戲。在遊戲裏每人都有一個固定的信息傳遞對象,其中,編號為i的同學的信息傳遞對象是編號為Ti同學。
遊戲開始時,每人都只知道自己的生日。之後每一輪中,所有人會同時將自己當前所知的生日信息告訴各自的信息傳遞對象(註意:可能有人可以從若幹人那裏獲取信息,但是每人只會把信息告訴一個人,即自己的信息傳遞對象)。當有人從別人口中得知自己的生日時,遊戲結束。請問該遊戲一共可以進行幾輪?
輸入輸出格式
輸入格式:
輸入共2行。
第1行包含1個正整數n表示n個人。
第2行包含n個用空格隔開的正整數T1,T2,……,Tn其中第i個整數Ti示編號為i
的同學的信息傳遞對象是編號為Ti的同學,Ti≤n且Ti≠i
數據保證遊戲一定會結束。
輸出格式:
輸出共 1 行,包含 1 個整數,表示遊戲一共可以進行多少輪。
輸入輸出樣例
輸入樣例#1:5 2 4 2 3 1輸出樣例#1:
3
說明
樣例1解釋
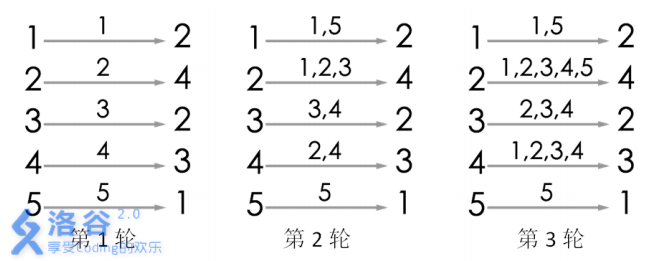
遊戲的流程如圖所示。當進行完第 3 輪遊戲後, 4 號玩家會聽到 2 號玩家告訴他自
己的生日,所以答案為 3。當然,第 3 輪遊戲後, 2 號玩家、 3 號玩家都能從自己的消息
來源得知自己的生日,同樣符合遊戲結束的條件。
對於 30%的數據, n ≤ 200;
對於 60%的數據, n ≤ 2500;
對於 100%的數據, n ≤ 200000。
tarjan求最小的環

#include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 210000 using namespace std; bool vis[N]; int n,m,tim,top,tot,sum; int dfn[N],low[N],ans[N],head[N],stack[N],belong[N]; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } struct Edge { int to,from,next; }edge[N]; int add(int x,int y) { tot++; edge[tot].to=y; edge[tot].next=head[x]; head[x]=tot; } int tarjan(int now) { dfn[now]=low[now]=++tim; stack[++top]=now; vis[now]=true; for(int i=head[now];i;i=edge[i].next) { int t=edge[i].to; if(vis[t]) low[now]=min(low[now],dfn[t]); else if(!dfn[t]) tarjan(t),low[now]=min(low[now],low[t]); } if(low[now]==dfn[now]) { sum++;belong[now]=sum;ans[sum]++; for(;stack[top]!=now;top--) belong[stack[top]]=sum,vis[stack[top]]=false,ans[sum]++; vis[now]=false; top--; } } int main() { n=read(); for(int i=1;i<=n;i++) m=read(),add(i,m); for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i); sort(ans+1,ans+1+sum); for(int i=1;i<=sum;i++) if(ans[i]!=1) { printf("%d",ans[i]); return 0; } }tarjan AC代碼
T3 鬥地主
題目描述
牛牛最近迷上了一種叫鬥地主的撲克遊戲。鬥地主是一種使用黑桃、紅心、梅花、方片的A到K加上大小王的共54張牌來進行的撲克牌遊戲。在鬥地主中,牌的大小關系根據牌的數碼表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色並不對牌的大小產生影響。每一局遊戲中,一副手牌由n張牌組成。遊戲者每次可以根據規定的牌型進行出牌,首先打光自己的手牌一方取得遊戲的勝利。
現在,牛牛只想知道,對於自己的若幹組手牌,分別最少需要多少次出牌可以將它們打光。請你幫他解決這個問題。
需要註意的是,本題中遊戲者每次可以出手的牌型與一般的鬥地主相似而略有不同。
具體規則如下:
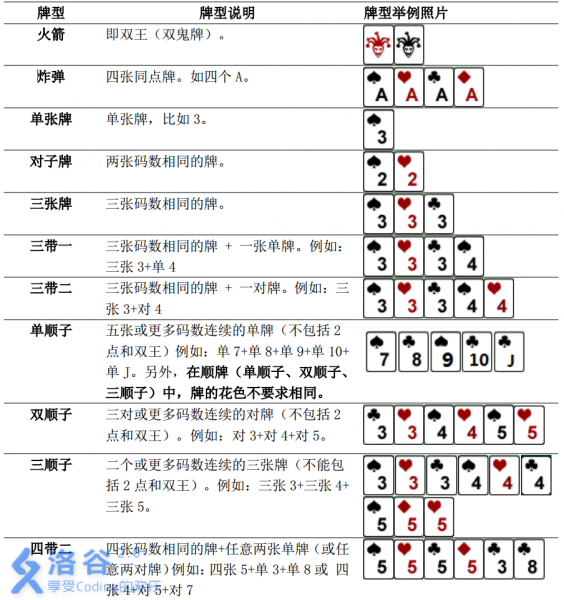
本題數據隨機,不支持hack,要hack或強力數據請點擊這裏
註意這裏4可以帶兩對
輸入輸出格式
輸入格式:
第一行包含用空格隔開的2個正整數T和n,表示手牌的組數以及每組手牌的張數。
接下來T組數據,每組數據n行,每行一個非負整數對aibi表示一張牌,其中ai示牌的數碼,bi表示牌的花色,中間用空格隔開。特別的,我們用1來表示數碼A,11表示數碼J,12表示數碼Q,13表示數碼K;黑桃、紅心、梅花、方片分別用1-4來表示;小王的表示方法為01,大王的表示方法為02。
輸出格式:
共T行,每行一個整數,表示打光第i手牌的最少次數。
輸入輸出樣例
輸入樣例#1:1 8 7 4 8 4 9 1 10 4 11 1 5 1 1 4 1 1輸出樣例#1:
3輸入樣例#2:
1 17 12 3 4 3 2 3 5 4 10 2 3 3 12 2 0 1 1 3 10 1 6 2 12 1 11 3 5 2 12 4 2 2 7 2輸出樣例#2:
6
說明
樣例1說明
共有1組手牌,包含8張牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通過打單順子(方片7,方片8,黑桃9,方片10,黑桃J),單張牌(黑桃5)以及對子牌(黑桃A以及方片A)在3次內打光。
對於不同的測試點, 我們約定手牌組數T與張數n的規模如下:
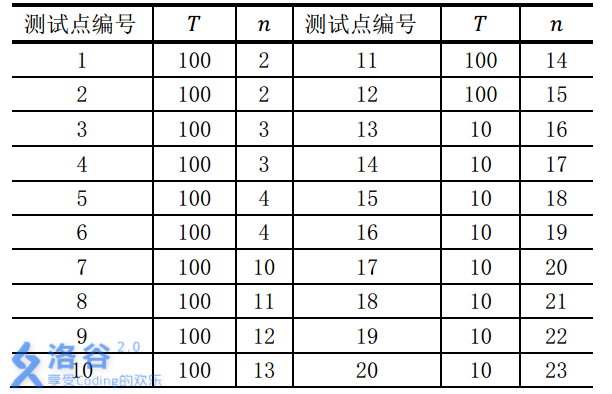
數據保證:所有的手牌都是隨機生成的。

zz啊、、開始的時候竟然讀錯題了!!! 以後絕對不能犯這種錯誤!!! #include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 1600 using namespace std; bool flag; int t,n,m,x,y,a[N],ans; int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } int main() { t=read();n=read(); while(t--) { ans=0;flag=false; memset(a,0,sizeof(a)); for(int i=1;i<=n;i++) { x=read();y=read(); a[x]++; } for(int i=0;i<=14;i++) if(a[i]>=3) {flag=true; ans=1;break;} if(!flag) for(int i=0;i<=14;i++) if(a[i]) ans++; printf("%d\n",ans); } return 0; }30分的部分分

#include<cstdio> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 25 using namespace std; int t,n,m,x,y,sum[N],card_num[N],ans,dp[N][N][N][N]; int sun_num[4]={0,5,3,2};//存儲我們要組成當前順子,最少需要的牌數 int read() { int x=0,f=1; char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1; ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘; ch=getchar();} return x*f; } int work(int s1,int s2,int s3,int s4,int king) { if(king==1) s1++,king=0;//如果只有一張王的話,我們只能將這張王看成1張單牌來處理 if(king==0) return dp[s4][s3][s2][s1];// else return min(dp[s4][s3][s2][s1+2],dp[s4][s3][s2][s1]+1);// } void dfs(int now)//now 為到當前狀態我們所出了幾次牌 { memset(sum,0,sizeof(sum)); if(now>ans) return ;//如果當前的出牌次數大於ans,return。我們要求最小的出牌次數 for(int i=2;i<=14;i++) sum[card_num[i]]++;//求出一共有幾張單牌,幾對雙牌,、、、 ans=min(ans,now+work(sum[1],sum[2],sum[3],sum[4],card_num[0]));//ans=當前已經出了的牌的次數+剩下的牌最少的出牌次數 for(int k=1;k<=3;k++) //找順子,順子一共有3種情況:單順子,雙順子,三順子 { for(int i=3;i<=14;i++) { int j; for(j=i;j<=14&&card_num[j]>=k;j++)//從當前牌開始到j 為順子,如果順子的排數小於k即不連續,continue { card_num[j]-=k; if(j-i+1>=sun_num[k]) dfs(now+1);//可以組成順子,出牌方案數+1;繼續搜索 } for(j--;j>=i;j--) card_num[j]+=k;//復原 } } } int main() { t=read();n=read(); /***********預處理處用dp[i][j][k][l]表示打出i套四張,j套三張,k套對拍,l張單拍要最少出幾次。*********/ memset(dp,1,sizeof(dp)); dp[0][0][0][0]=0; for(int i=0;i<=n;i++)//4 for(int j=0;j<=n;j++) //3 for(int k=0;k<=n;k++)//2 for(int l=0;l<=n;l++)//1 if(i*4+j*3+k*2+l*1<=n) { if(i)//有四張的牌 { if(k>=2) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k-2][l]+1);//4帶兩對不一樣的對牌 if(l>=2) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k][l-2]+1);//4帶單張牌(四帶二) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i-1][j][k][l]+1);//炸彈,不帶任何牌 } if(j)//處理處有三張相同的牌時可以出的最少次數 { if(k) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k-1][l]+1);//三帶一對 if(l) dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k][l-1]+1);//三帶一 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j-1][k][l]+1);//三張牌,什麽也不帶 } if(k)//兩張牌 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j][k-1][l]+1);//對子 if(l)//單張牌 dp[i][j][k][l]=min(dp[i][j][k][l],dp[i][j][k][l-1]+1);//單張牌 } /*************************************預處理部分************************************************/ while(t--) { memset(card_num,0,sizeof(card_num)); ans=n; for(int i=1;i<=n;i++) { x=read(),y=read(); if(x==1) card_num[14]++;//這個地方的存儲使我們後面找順子的時候比較方便,因為順子最大到A else card_num[x]++; } dfs(0); printf("%d\n",ans); } return 0; }dp預處理+dfs
小感:唉,zz!明明可以拿230的但是只拿了170~~~~(>_<)~~~~ 第一題忘記開了個結構體,數組開小了,丟了30分,第三題n的輸入寫在了while的裏面,然後TLE了!!
這告訴我們noip的時候一定要仔細讀題!數組的大小再開的時候一定要慎重,看好數據範圍以及數組內存的是什麽東西,然後在寫數組的大小!!
一定要讀清題目,好好讀題,明白題目中的每個變量代表的什麽,什麽表示什麽、多讀幾遍題目!看清怎麽輸入!
noip 2015 day1

