NOIP 2015 DAY2
跳石頭
題目背景
一年一度的“跳石頭”比賽又要開始了!
題目描述
這項比賽將在一條筆直的河道中進行,河道中分布著一些巨大巖石。組委會已經選擇好了兩塊巖石作為比賽起點和終點。在起點和終點之間,有 N 塊巖石(不含起點和終 點的巖石)。在比賽過程中,選手們將從起點出發,每一步跳向相鄰的巖石,直至到達 終點。
為了提高比賽難度,組委會計劃移走一些巖石,使得選手們在比賽過程中的最短跳 躍距離盡可能長。由於預算限制,組委會至多從起點和終點之間移走 M 塊巖石(不能 移走起點和終點的巖石)。
輸入輸出格式
輸入格式:
輸入文件名為 stone.in。
輸入文件第一行包含三個整數 L,N,M,分別表示起點到終點的距離,起點和終 點之間的巖石數,以及組委會至多移走的巖石數。
接下來 N 行,每行一個整數,第 i 行的整數 Di(0 < Di < L)表示第 i 塊巖石與 起點的距離。這些巖石按與起點距離從小到大的順序給出,且不會有兩個巖石出現在同 一個位置。
輸出格式:
輸出文件名為 stone.out。 輸出文件只包含一個整數,即最短跳躍距離的最大值。
輸入輸出樣例
輸入樣例#1:25 5 2 2 11 14 17 21輸出樣例#1:
4
說明
輸入輸出樣例 1 說明:將與起點距離為 2 和 14 的兩個巖石移走後,最短的跳躍距離為 4(從與起點距離 17 的巖石跳到距離 21 的巖石,或者從距離 21 的巖石跳到終點)。
另:對於 20%的數據,0 ≤ M ≤ N ≤ 10。 對於50%的數據,0 ≤ M ≤ N ≤ 100。
對於 100%的數據,0 ≤ M ≤ N ≤ 50,000,1 ≤ L ≤ 1,000,000,000。
#include<iostream> #include<cstdio> using namespace std; int n,m,L; int a[50005],ans; int check(int x) { int last=0,cnt=0; for(int i=0;i<=n;i++) {if(a[i]-last<x){cnt+=1;continue;} last=a[i]; } if(cnt>m) return 0; return 1; } int main() { scanf("%d%d%d",&L,&n,&m); for(int i=0;i<n;i++) scanf("%d",&a[i]); a[n]=L; int r=L,l=1; while(l<=r) { int mid=(l+r)/2; if(check(mid)){ans=mid;l=mid+1;} else r=mid-1; } printf("%d\n",ans); return 0; }
子串
題目背景
無
題目描述
有兩個僅包含小寫英文字母的字符串 A 和 B。現在要從字符串 A 中取出 k 個互不重疊的非空子串,然後把這 k 個子串按照其在字符串 A 中出現的順序依次連接起來得到一 個新的字符串,請問有多少種方案可以使得這個新串與字符串 B 相等?註意:子串取出 的位置不同也認為是不同的方案。
輸入輸出格式
輸入格式:
輸入文件名為 substring.in。
第一行是三個正整數 n,m,k,分別表示字符串 A 的長度,字符串 B 的長度,以及問
題描述中所提到的 k,每兩個整數之間用一個空格隔開。 第二行包含一個長度為 n 的字符串,表示字符串 A。 第三行包含一個長度為 m 的字符串,表示字符串 B。
輸出格式:
輸出文件名為 substring.out。 輸出共一行,包含一個整數,表示所求方案數。由於答案可能很大,所以這裏要求[b]輸出答案對 1,000,000,007 取模的結果。[/b]
輸入輸出樣例
輸入樣例#1:6 3 1 aabaab aab輸出樣例#1:
2輸入樣例#2:
6 3 2 aabaab aab輸出樣例#2:
7輸入樣例#3:
6 3 3 aabaab aab輸出樣例#3:
7
說明

對於第 1 組數據:1≤n≤500,1≤m≤50,k=1;
對於第 2 組至第 3 組數據:1≤n≤500,1≤m≤50,k=2; 對於第 4 組至第 5 組數據:1≤n≤500,1≤m≤50,k=m; 對於第 1 組至第 7 組數據:1≤n≤500,1≤m≤50,1≤k≤m; 對於第 1 組至第 9 組數據:1≤n≤1000,1≤m≤100,1≤k≤m; 對於所有 10 組數據:1≤n≤1000,1≤m≤200,1≤k≤m。
/* 狀態f[i][j][k] 表示A串匹配到i B串匹配到j 用了k個子串 轉移的話 f[i][j][k]=f[i-1][j-1][k]+f[i-1][j-1][k-1]分別表示i是不是建立了一個新的子串 當然這是我們會發現 這樣的狀態是默認了i用了 顯然i可以不用 也就是說這樣就遺漏了許多狀態 我們重新定義一下他 加一維01表示i用了沒用 f[i][j][k][0或1] 這樣轉移就要分開考慮01 f[i][j][k][0]=f[i-1][j][k][0]+f[i-1][j][k][1]因為i沒有用 所以不會有新串k不變 B串也不會更新匹配j不變 f[i][j][k][1]=f[i-1][j-1][k-1][0]+f[i-1][j-1][k][1]+f[i-1][j-1][k-1][1] */ #include<iostream> #include<cstring> #include<cstdio> #define mod 1000000007 #define maxn 210 using namespace std; int n,m,p,s,f[2][maxn][maxn][2]; char A[maxn*5],B[maxn]; int main() { scanf("%d%d%d",&n,&m,&p); scanf("%s%s",A+1,B+1); for(int i=1;i<=n;i++) { f[i%2][1][1][0]=s; if(A[i]==B[1]) f[i%2][1][1][1]=1,s++; for(int j=2;j<=m;j++) for(int k=1;k<=p;k++) { f[i%2][j][k][0]=(f[(i+1)%2][j][k][0]+f[(i+1)%2][j][k][1])%mod; if(A[i]==B[j]) f[i%2][j][k][1]=((f[(i+1)%2][j-1][k-1][1]+f[(i+1)%2][j-1][k][1])%mod +f[(i+1)%2][j-1][k-1][0])%mod; } for(int j=1;j<=m;j++) for(int k=1;k<=p;k++) f[(i+1)%2][j][k][1]=0,f[(i+1)%2][j][k][0]=0; } printf("%d\n",(f[n%2][m][p][0]+f[n%2][m][p][1])%mod); return 0; }
運輸計劃
題目背景
公元 2044 年,人類進入了宇宙紀元。
題目描述
L 國有 n 個星球,還有 n-1 條雙向航道,每條航道建立在兩個星球之間,這 n-1 條航道連通了 L 國的所有星球。
小 P 掌管一家物流公司,該公司有很多個運輸計劃,每個運輸計劃形如:有一艘物
流飛船需要從 ui 號星球沿最快的宇航路徑飛行到 vi 號星球去。顯然,飛船駛過一條航道 是需要時間的,對於航道 j,任意飛船駛過它所花費的時間為 tj,並且任意兩艘飛船之 間不會產生任何幹擾。
為了鼓勵科技創新,L 國國王同意小 P 的物流公司參與 L 國的航道建設,即允許小 P 把某一條航道改造成蟲洞,飛船駛過蟲洞不消耗時間。
在蟲洞的建設完成前小 P 的物流公司就預接了 m 個運輸計劃。在蟲洞建設完成後, 這 m 個運輸計劃會同時開始,所有飛船一起出發。當這 m 個運輸計劃都完成時,小 P 的 物流公司的階段性工作就完成了。
如果小 P 可以自由選擇將哪一條航道改造成蟲洞,試求出小 P 的物流公司完成階段 性工作所需要的最短時間是多少?
輸入輸出格式
輸入格式:
輸入文件名為 transport.in。
第一行包括兩個正整數 n、m,表示 L 國中星球的數量及小 P 公司預接的運輸計劃的數量,星球從 1 到 n 編號。
接下來 n-1 行描述航道的建設情況,其中第 i 行包含三個整數 ai, bi 和 ti,表示第
i 條雙向航道修建在 ai 與 bi 兩個星球之間,任意飛船駛過它所花費的時間為 ti。
接下來 m 行描述運輸計劃的情況,其中第 j 行包含兩個正整數 uj 和 vj,表示第 j個 運輸計劃是從 uj 號星球飛往 vj 號星球。
輸出格式:
輸出 共1行,包含1個整數,表示小P的物流公司完成階段性工作所需要的最短時間。
輸入輸出樣例
輸入樣例#1:6 3 1 2 3 1 6 4 3 1 7 4 3 6 3 5 5 3 6 2 5 4 5輸出樣例#1:
11
說明
所有測試數據的範圍和特點如下表所示
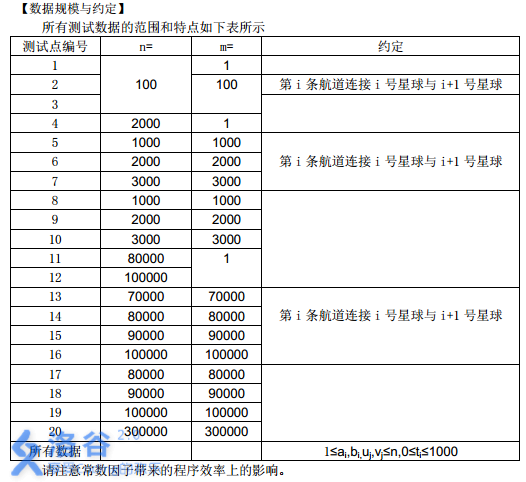
請註意常數因子帶來的程序效率上的影響。

#include<iostream> #include<cstdio> #include<cstring> #define N 100001 using namespace std; int head[N<<1],t[N],f[N][25],g[N][25],sum[N],deep[N]; int n,m,x,y,z,ans,tot,cnt,tmp; struct edge { int u,to,next,dis; }e[N<<1]; inline int read() { int x=0,f=1;char c=getchar(); while(c>‘9‘||c<‘0‘){if(c==‘-‘)f=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();} return x*f; } inline void add(int u,int to,int dis) { e[++cnt].to=to;e[cnt].next=head[u];e[cnt].dis=dis;head[u]=cnt; } inline void get_fa() { for(int j=1;j<=22;j++) for(int i=1;i<=n;i++) { f[i][j]=f[f[i][j-1]][j-1]; g[i][j]=max(g[i][j-1],g[f[i][j-1]][j-1]); } } void dfs(int now,int fa,int c,int wa) { f[now][0]=fa;deep[now]=c;g[now][0]=wa;sum[now]+=wa; for(int i=head[now];i;i=e[i].next) { int v=e[i].to; if(v!=fa) { sum[v]+=sum[now]; dfs(v,now,c+1,e[i].dis); } } } int lca(int a,int b) { if(deep[a]<deep[b]) swap(a,b); int t=deep[a]-deep[b]; for(int i=0;i<=22;i++) { if(t&(1<<i)) { tmp=max(g[a][i],tmp); a=f[a][i]; } } if(a==b) return a; for(int i=21;i>=0;i--) { if(f[a][i]!=f[b][i]) { tmp=max(tmp,g[a][i]); tmp=max(tmp,g[b][i]); a=f[a][i];b=f[b][i]; } } tmp=max(tmp,max(g[a][0],g[b][0])); return f[a][0]; } int main() { n=read();m=read(); if(m==1) { for(int i=1;i<n;++i) { x=read();y=read();z=read(); add(x,y,z);add(y,x,z); } dfs(1,1,0,0);get_fa(); x=read();y=read();int L=lca(x,y); ans=sum[x]+sum[y]-2*sum[L]-tmp; printf("%d\n",ans); } return 0; }20暴力
/* 最後一個點T了 qian lv ji qiong 了 沒學過樹剖 聽chx聽xzc說的神奇的方法 Orz 首先求出每個計劃的路徑長度 這裏寫的倍增 然後二分答案 對於每個ans 統計>他的路徑條數 tot 並維護與ans的最大差值 dec 並且對於每條不合法的路徑維護每個點的經過次數 然後枚舉點 如果經過次數==tot說明每一條不合法的都經過他 然後嘗試把它建成蟲洞 如果他對應邊的權值>=dec 那麽我們刪掉它ans就合法了 關鍵是統計每個點在非法路徑中的經過次數 : 維護sum數組 對於每個非法的路徑起點a b LCA(a,b)==s sum[a]++ sum[b]++ sum[s]-=2 這樣網上更新的話 經過的點的sum值都變成1 祖先s的變成0 這樣就實現了sum數組的維護 */ #include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #define maxn 300100 using namespace std; int n,m,num,head[maxn],ans,inf; int fa[maxn][30],dep[maxn],dis[maxn],sum[maxn],edge[maxn]; struct node { int u,v,t,pre; }e[maxn*2]; struct Ans { int ai,bi,anc,di; }lca[maxn]; int init() { int x=0;char s=getchar(); while(s<‘0‘||s>‘9‘)s=getchar(); while(s>=‘0‘&&s<=‘9‘){x=x*10+s-‘0‘;s=getchar();} return x; } void Add(int from,int to,int dis) { num++; e[num].u=from; e[num].v=to; e[num].t=dis; e[num].pre=head[from]; head[from]=num; } void Dfs(int now,int from,int c,int Dis) { fa[now][0]=from; dep[now]=c;dis[now]=Dis; for(int i=head[now];i;i=e[i].pre) if(e[i].v!=from) { edge[e[i].v]=i; Dfs(e[i].v,now,c+1,Dis+e[i].t); } } void Get_fa() { for(int j=1;j<=16;j++) for(int i=1;i<=n;i++) fa[i][j]=fa[fa[i][j-1]][j-1]; } int Get_same(int a,int t) { for(int i=0;i<16;i++) if(t&(1<<i)) a=fa[a][i]; return a; } int LCA(int a,int b) { if(dep[a]<dep[b])swap(a,b); a=Get_same(a,dep[a]-dep[b]); if(a==b)return a; for(int i=16;i>=0;i--) if(fa[a][i]!=fa[b][i]) { a=fa[a][i]; b=fa[b][i]; } return fa[a][0]; } void Init() { n=init();m=init(); int u,v,t; for(int i=1;i<=n-1;i++) { u=init();v=init();t=init(); Add(u,v,t);Add(v,u,t); } Dfs(1,1,0,0); Get_fa(); for(int i=1;i<=m;i++) { lca[i].ai=init();lca[i].bi=init(); lca[i].anc=LCA(lca[i].ai,lca[i].bi); lca[i].di=dis[lca[i].ai]+dis[lca[i].bi]-2*dis[lca[i].anc]; inf=max(inf,lca[i].di); } } void Up_sum(int now,int from) { for(int i=head[now];i;i=e[i].pre) if(e[i].v!=from) { Up_sum(e[i].v,now); sum[now]+=sum[e[i].v]; } } int Judge(int x) { memset(sum,0,sizeof(sum)); int tot=0,dec=0; for(int i=1;i<=m;i++) if(lca[i].di>x)//非法路徑 { tot++; dec=max(dec,lca[i].di-x);//最長非法路徑與ans差值 sum[lca[i].ai]++; sum[lca[i].bi]++; sum[lca[i].anc]-=2; } Up_sum(1,1);//更新sum數組 for(int i=1;i<=n;i++) if(tot==sum[i]&&e[edge[i]].t>=dec)//刪掉edge[i]這條邊之後答案合法了 return 1; return 0; } void Solve()//二分答案 { int l=0,r=inf; while(l<=r) { int mid=(l+r)/2; int tmp=Judge(mid); if(tmp==1) { r=mid-1; ans=mid; } else l=mid+1; } } void Printf() { printf("%d\n",ans); } int main() { Init(); Solve(); Printf(); return 0; }

/* 實在羞於打上自己的分數:10+10+20=40; 試問一下,這要是放在考場上呢?!讀錯題,沒考慮全面是理由嗎!!! T1 10分!!以前還做過。T2連hash暴力都寫掛...我不想多數什麽,dp方程沒有耐心推,暴力沒耐心調。連個小數據都舍不得造! 很基礎的東西都忘了怎麽寫! 不管怎樣,這就noip了,希望自己有數,提高效率!!!耐心 。 */conclusion
NOIP 2015 DAY2

