定義

　　由一個決策圖和可能的結果（包括資源成本和風險組成），用來創建到達目的的規劃。——維基百科

通俗理解

　　給定一個輸入值，從樹節點不斷往下走，直至走到葉節點，這個葉節點就是對輸入值的一個預測或者分類。

算法分類

ID3（Iterative Dichotomiser 3，叠代二叉樹3代）

歷史

　　ID3算法是由Ross Quinlan發明的用於生成決策樹的算法，此算法建立在奧卡姆剃刀上。奧卡姆剃刀又稱為奧坎的剃刀，意為簡約之法則，也就是假設越少越好，或者“用較少的東西，同樣可以做好的事情”，即越是小型的決策樹越優於大的決策樹。當然ID3它的目的並不是為了生成越小的決策樹，這只是這個算法的一個哲學基礎。

引入

　　信息熵。熵是熱力學中的概念，是一種測量在動力學方面不能做功的能量總數，也就是當總體熵的增加，其做功能力也下降，熵的量度正是能量退化的指標——維基百科。香農將“熵”的概念引入到了信息論中，故在信息論中被稱為信息熵，它是對不確定性的測量，熵越高，不確定性越大，熵越低，不確定性越低。

　　那麽到底何為“信息熵”？它是衡量信息量的一個數值。那麽何又為“信息量”？我們常常聽到某段文字信息量好大，某張圖信息量好大，實際上指的是這段消息（消息是信息的物理表現形式，信息是其內涵——《通信原理》）所包含的信息很多，換句話說傳輸信息的多少可以采用“信息量”去衡量。這裏的消息和信息並不完全對等，有可能出現消息很大很多，但所蘊含有用的信息很少，也就是我們常說的“你說了那麽多（消息多），但對我來說沒用（信息少，即信息量少）”。這也進一步解釋了消息量的定義是傳輸信息的多少。

　　進一步講，什麽樣的消息才能構成信息呢？

　　我們為什麽會常常發出感嘆“某段文字的信息量好大”，得到這條消息時是不是有點出乎你的意料呢？比如，X男和X男在同一張床上發出不可描述的聲音，這段消息對於你來講可能就會發出“信息量好大”的感嘆。再比如，某情侶在同一張床上發出不可描述的聲音，這段消息對於你來講可能就是家常便飯，並不會發出“信息量好大”的感嘆。前一個例子的消息中所構成的信息很大，後一個例子的消息中所構成的信息很小，這是因為，只有消息中不確定的內容才構成的消息才構成信息。消息所表達的事件越不可能發生，越不可預測，就會越使人感到驚訝和意外，信息量就越大——《通信原理》。

　　我們解釋了消息、信息、信息量之間的關系。回到信息熵上來之前，我們還得繼續上面的話題，上面提到了“事件發生的可能性”，這很理所當然的是可以以出現的概率來描述，也就是說我們現在更進一步，信息量與消息中事件發生的概率相關，上面的例子就可以這麽描述：消息中的事件發生概率越小，信息量越大，消息中的事件發生的概率越大，信息量就越小。

　　而信息熵是接收的每條消息中的包含的信息的平均值，數學上也就是信息量的期望，也就是在結果出來之前對可能產生的信息量的期望。

　　最後小結，如果熵很大，也就是信息量的期望大，也就是事件的概率小，更或者事件的不確定性大。

　　先給出信息熵的公式：，X為隨機變量，其值域為{}，其中P為X的概率質量函數。下面我們來逐步推導出這個公式（據《通信原理》）：

1. 非負性。消息中所含信息量就是該消息中的事件所出現的概率：
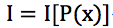
2. 單調性。概率越大，消息量越小，P(x)=1，I=0；P(x)=0，I=∞，完全不可能發生的事情它的信息量就很大很大，例如太陽西邊生氣了這種事情。

3. 累加性。若幹個相互獨立事件構成的消息，所含信息量等於各獨立事件消息量之和，消息量具有可加性：

4. 綜上，滿足以上三個性質的公式,香農將信息量定義為：

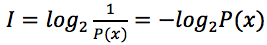
5. 信息熵是信息量的期望，也就是，離散型隨機變量的期望也即是統計平均值，是試驗中每次可能的結果乘以其結果概率的綜合，那麽

定義

　　在引入了信息熵這個概念後，接著開始正式介紹ID3算法。在算法的每次叠代中，它遍歷數據集每個未使用的屬性，並計算該屬性的熵H(S)（或信息增益IG(S)），接著選取熵最小的屬性（或信息增益最大的屬性），根據選擇的屬性對樣本進行分類。（On each iteration of the algorithm, it iterates through every unused attribute of the set S and calculates the entropy H(S) (or information gain IG(S)) of that attribute. It then selects the attribute which has the smallest entropy (or largest information gain) value. The set S}is then split by the selected attribute (e.g. age is less than 50, age is between 50 and 100, age is greater than 100) to produce subsets of the data.——wikipekia）對於ID3，實際上是計算信息熵的一個過程，選擇信息熵最低的屬性或者稱為特征，當然通常是計算信息增益，下面給出公式及推導過程。

公式及推導過程

　　信息增益：IG(A) = H(D) – H(D|A)。D表示樣本集，A表示屬性（或特征），IG(A)表示特征A的信息增益，H(D)表示樣本的信息熵，H(D|A)表示特征A對樣本集D的經驗條件熵（即條件概率分布）。
　　信息熵在前面已經介紹過，對於經驗條件熵，只需回顧一下條件概率分布。
　　對於離散型隨機變量X和Y，隨機變量Y在條件{X = x}下的條件概率分別是：，表示X和Y的聯合分布概率，即“X=i，並且Y=j發生的概率”，這是數學公式。

　　對於條件熵H(Y|X=x)為變數Y在變數X取特定值x條件下的熵，那麽H(Y|X)就是H(Y|X=x)在X取遍所有x後平均的結果。那麽可得出以下公式推導：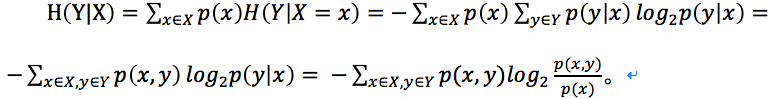

　　整個推導過程和條件概率分布公式息息相關。
　　最後也即得出信息增益的公式：，代入即可。

　　給出《機器學習》中的公式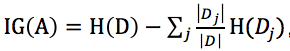：，其中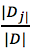充當第j個分區的權重。

練習

　　一共有14個樣本數據D，且有年齡、收入、是否是學生、信用評級4個特征，分類為是否可能購買電腦。計算樣本數據的信息熵以及各個特征的信息增益。

　　根據信息熵公式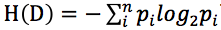：可得：（py表示購買電腦的概率，pn表示不購買電腦的概率）

　　接下來計算年齡的條件熵：

　　其中低年齡占5/14，且購買電腦占2/5，不能購買電腦占3/5；

　　中年齡占4/14，且購買電腦占4/4，不能購買電腦占0/4；
　　高年齡占5/14，且購買電腦占3/5，不能購買電腦占2/5。

　　根據條件熵的計算公式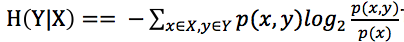：可得：

　　關於條件熵這裏要再多加解釋一下公式，在本例中X表示年齡且X={低，中，高}，也就是說X要取完這三個值，在這三個值的條件確定下Y的條件熵，而Y表示是否購買電腦且Y={是，否}，換算成公式即是：。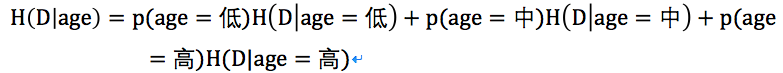

　　上面我們已經計算過，H(D)=0.94那麽：

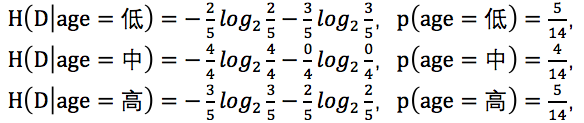
　　可得：

　　，依次計算出每個特征的信息增益，選取信息增益最大的特征作為分裂特征。接著再遞歸計算信息增益形成一棵樹決策樹。

C4.5

歷史

　　此算法也是由ID3算法的發明者Ross Quinlan所發明，我查了資料沒有找到為什麽取名叫C4.5，維基百科上的解釋也是successor of ID3，只說明了它是ID3算法的改進，同時也還有C5.0。

引入

　　信息增益率。既然是ID3算法的改進，那說明它們既有相同點也有不同點，相同點就是同樣是基於信息熵，不同點就是ID3使用的是信息增益來作為選擇分裂特征，而C4.5使用的則是信息增益率。
　　之所以會有ID3的改進，是因為ID3使用信息增益時如果某個特征數目較多很有可能對此特征有所偏好，改用信息增益率就會減少這種影響。
　　在前面我們介紹了信息熵以及信息增益，那麽什麽又是信息增益率呢？信息增益率使用一個叫做“分裂信息”值將信息增益規範化，分類信息的公式為：

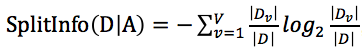，和信息增益有點類似。

定義

　　C4.5同ID3類似，不同的只是選擇分裂特征的方式不同，C4.5引入的是“信息增益率”來選擇，選擇信息增益率大的特征，參考ID3算法定義。

公式及推導過程

　　上面引入了信息增益率，開頭我們提到了C4.5不直接只用“信息增益”來選擇分裂特征，而是通過“信息增益率”，而信息增益率是在信息增益的基礎上除以分類信息。

　　，信息增益IG(A)以及分裂信息SplitInfo(D|A)均已給出，此處不再重復。

練習

　　還是ID3中的例子，在ID3的例子中我們已經計算了特征為age時的信息增益，我們只需再計算出特征age的分裂屬性即可。

　　當然增益率就根據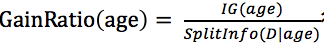得出。

　　具體數值以及其他特征的增益率不再給出，選擇增益率最大的特征。

CART(Classification and Regression Trees，分類回歸樹)

歷史

　　ID3、C4.5和CART都是決策樹模型的經典算法。決策樹不僅可以用來分類，同時它也可以做回歸，CART就是既可以用作分類也可以用作回歸。它是由Leo Breiman, Jerome Friedman, Richard Olshen與Charles Stone於1984年提出的。

引入

　　基尼（Gini）指數。與ID3和C4.5通過信息熵來確定分裂特征不同，CART通過一個叫基尼指數的東西來確定分裂特征。
　　在經濟學中也有一個基尼系數（或基尼指數），我暫時未找到這兩者之間有沒有什麽聯系，或者這裏的基尼指數是否引自經濟學。
　　基尼指數和信息熵類似，都是數值越大其不確定性越大，之所以選用基尼指數是因為相對於信息熵的計算更快一些。

定義

　　CART是一個分類及回歸的算法，使用基尼指數小的特征作為分裂特征。

公式及推導過程

　　CART算法其核心公式就是基尼指數的計算，基尼指數越大不確定越大，基尼指數的計算公式為：

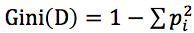　　，其中pi是D中元組中Ci類的概率。

練習

　　現在有10個樣本，其中有是否有房、婚姻狀況、年收入3個特征，根據這三個特征來判斷是否拖欠貸款。

　　先選取是否有房這個特征來計算它的基尼指數。

　　可知有房者占3/10，其中未拖欠貸款占3/3，拖欠貸款占0/3;
　　無房者占7/10，其中未拖欠貸款占4/7，拖欠貸款占3/7;

　　有房者的基尼指數記為;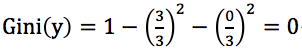

　　無房者的基尼指數記為;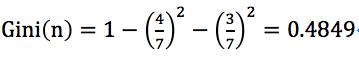

　　是否有房的基尼指數為。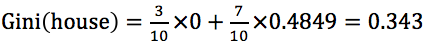

　　以此計算各個特征的基尼指數，選取最小的作為分裂特征。

　　機器學習中有關決策樹相關的理論方面大致已經介紹完畢，實際上是主要介紹了ID3、C4.5、CART三種算法，對於決策樹並沒有很詳盡的理論講解，例如構造過程剪枝等。在後面對決策樹的學習中隨時再來舔磚加瓦，也請看到此篇博客的朋友能給予指點。

決策樹（理論篇）