Convex optimization 凸優化
zh.wikipedia.org/wiki/凸優化
以下問題都是凸優化問題,或可以通過改變變量而轉化為凸優化問題:[5]
- 最小二乘
- 線性規劃
- 線性約束的二次規劃
- 半正定規劃
Convex function
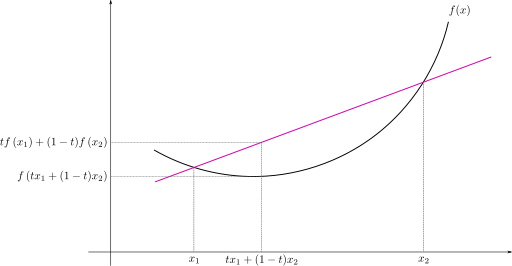
Convex minimization is a subfield of optimization that studies the problem of minimizing convex functions over convex sets. The convexity makes optimization easier than the general case since local minimum must be a global minimum, and first-order conditions are sufficient conditions for optimality.[1]
Convex optimization 凸優化
相關推薦
CMU Convex Optimization(凸優化)筆記1--凸集和凸函數
lock element lane 向量 最大化 intersect sca 對數 adr CMU凸優化筆記--凸集和凸函數 結束了一段時間的學習任務,於是打算做個總結。主要內容都是基於CMU的Ryan Tibshirani開設的Convex Optimization課程做
Convex optimization 凸優化
cas gen img 問題: 最小二乘 fun min link roc zh.wikipedia.org/wiki/凸優化 以下問題都是凸優化問題,或可以通過改變變量而轉化為凸優化問題:[5] 最小二乘 線性規劃 線性約束的二次規劃 半正定規劃
為什麼 Non-Convex Optimization (非凸優化)受到了越來越大的關注?
前言:運籌學在國內,遠沒有統計和人工智慧來的普及。相信很多人不知道,運籌學正是研究優化理論的學科,而人工智慧最後幾乎都能化簡成求解一個能量/損失函式的優化問題。因此,我把它稱為人工智慧、大資料的“引擎”。 本文的詳細版本已發表在我的專欄: 離散/整數/組合/非凸優化概述及其在AI的應用 - 知乎專欄 言
凸優化簡介 Convex Optimization Overview
最近的看的一些內容好多涉及到凸優化,沒時間系統看了,簡單的瞭解一下,凸優化的兩個基本元素分別是凸函式與凸包 凸集 凸集定義如下: 也就是說在凸集內任取兩點,其連線上的所有點仍在凸集之內。 凸函式 凸函式的定義如下: θx+(1−θ)yθx+(1−θ)y
凸優化(Convex Optimization)是什麼?
”凸優化“ 是指一種比較特殊的優化,是指求取最小值的目標函式為凸函式的一類優化問題。其中,目標函式為凸函式且定義域為凸集的優化問題稱為無約束凸優化問題。而目標函式和不等式約束函式均為凸函式,等式約束函式為仿射函式,並且定義域為凸集的優化問題為約束優化問題 。一、什麼是凸優化不
【Convex Optimization (by Boyd) 學習筆記】Chapter 2 - Convex sets(1) 仿射集&凸集
I. 仿射凸集(Affine and convex sets) 1. 線與線段 假設\(R^n\)空間內兩點\(x_1,x_2\, (x_1≠x_2)\),那麼\(y=\theta x_1+(1-\theta)x_2, \theta∈R\)表示從x1到x2的線。而當\(0≤\theta≤1\)時,表示x1
關於凸優化的一些簡單概念
mage 不等式 -c 集合 repl ont mil www 條件 http://www.cnblogs.com/tornadomeet/p/3300132.html 沒有系統學過數學優化,但是機器學習中又常用到這些工具和技巧,機器學習中最常見的優化當屬凸優化了,這
凸優化
置信度 新的 wid borde tab 最小化 最大熵 logistic gist 機器學習中的大多數問題可以歸結為最優化問題。把一些典型的問題用最優化的方法建立數學模型,再最優化的方式求解。 我們再看看數據挖掘和機器學習中哪些是最優化問題,哪些不是。 名
凸優化&非凸優化問題
spa 1-1 參考 margin 問題 quest log ima image 轉載知乎大神的回答:Robin Shen 參考:https://www.zhihu.com/question/20343349 凸優化&非凸
凸優化概念
分享 height gpo 優化 post 兩個 線上 技術 滿足 參考:https://www.cnblogs.com/harvey888/p/7100815.html 1、凸集 對於一個集合C,若任意及,都有: 幾何意義表現為: 如果集合C上的任意兩個點的連線也在C集
斯坦福凸優化課程Video2.4
bubuko 2.4 所有 gpo 條件 平面 alt 集合 分開 title: 斯坦福凸優化課程Video2-4 tags: note notebook: 6- 英文課程-14-convex optimization --- 斯坦福凸優化課程Video2-4 超平面分離
斜率凸優化小結
技術 樹形 元素 .org 進行 mat 分割 best img 斜率凸優化小結 前言 很久以前考了一道叫做"林克卡特樹"的題目( 還記得被八省聯考支配的恐懼嗎?) 正解是用直線去切一個凸函數...... 當時並不是很會。然而\(APIO\)講課竟然講了
【CF125E】MST Company(凸優化,最小生成樹)
als space false truct main math tdi 給人 kruskal 【CF125E】MST Company(凸優化,最小生成樹) 題面 洛谷 CF 題解 第一眼看見就給人麗潔姐那道\(tree\)一樣的感覺。 那麽二分一個權值,加給所有有一個端點是
非凸優化的方法
本質 最小化 條件 detail art hang 約束 article 結構 關於非凸優化的方法, https://blog.csdn.net/kebu12345678/article/details/54926287 提到,可以把非凸優化轉換為凸優化,通過修改一些條件。
[JZOJ5641] 林克卡特樹【樹形DP】【凸優化】
Description 給定一棵n個節點的樹,邊有邊權(可能為負)。 你需要刪掉恰好K條邊,再連上恰好K條邊權為0的邊,並保證連完邊後這還是一棵樹,求這棵樹的最大的最長路長度。 K
凸優化、最優化、凸集、凸函式
原文:https://www.cnblogs.com/AndyJee/p/5048735.html 我們知道壓縮感知主要有三個東西:訊號的稀疏性,測量矩陣的設計,重建演算法的設計。那麼,在重建演算法中,如何對問題建立數學模型並求解,這就涉及到了最優化或凸優化的相關知識。
一種基於凸優化的影象去噪方法演示
本文介紹一種基於凸優化的影象去噪方法。 該方法採用L1範數來衡量影象的平滑度,即能濾除澡聲,又能最大限度地儲存影象的邊緣。 模型如下: 其中f(x)為差分矩陣,存放了X每個元素與其4鄰域的差值。 I為輸入的灰度影象。 對於三通道彩色影象,可
[BZOJ1150]-[CTSC2007]資料備份Backup-dp凸優化
說在前面 凸優化真好用 然而二分上下界me從來都沒有一次性對過 撒幣DP都能寫錯,各種細節錯 me怕是廢了 題目 洛谷P3620傳送門 BZOJ1150傳送門 看題可戳傳送門 解法 首先兩維的DP是很好想的 然後yy一下,或者打個表,發現這個
凸優化和非凸優化
數學中最優化問題的一般表述是求取,使,其中是n維向量,是的可行域,是上的實值函式。 凸優化問題是指: 是閉合的凸集且是上的凸函式的最優化問題,這兩個條件任一不滿足則該問題即為非凸的最優化問題。
最大間隔轉為二次凸優化問題daidingdaiding
計算最大間隔:兩者等價,。 最小化 SVM的目標函式:上述的函式,很明顯是線性約束的二次規劃問題(即凸優化問題)。因目標函式是凸函式,約束是線性的,而且是二次形式。這是典型的二次規劃問題。可知,只要轉為凸優化問題,即該問題可以解決了。 (1)、
