P1661 擴散

題目描述

一個點每過一個單位時間就會向四個方向擴散一個距離，如圖。

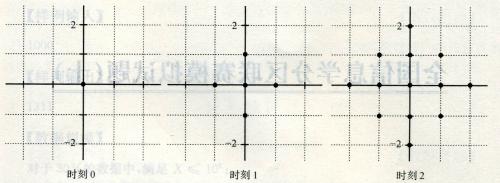
兩個點a、b連通，記作e(a,b),當且僅當a、b的擴散區域有公共部分。連通塊的定義是塊內的任意兩個點u、v都必定存在路徑e(u,a0),e(a0,a1),…,e(ak,v)。給定平面上的n給點，問最早什麽時刻它們形成一個連通塊。

輸入輸出格式

輸入格式：

第一行一個數n，以下n行，每行一個點坐標。

【數據規模】

對於20%的數據，滿足1≤N≤5; 1≤X[i],Y[i]≤50;

對於100%的數據，滿足1≤N≤50; 1≤X[i],Y[i]≤10^9。

輸出格式：

一個數，表示最早的時刻所有點形成連通塊。

輸入輸出樣例

2
0 0
5 5

5

分析：

離散化，最短距離就是映射在x軸和y軸上的距離和除2。

比如說一個點是(5,0)，一個點是(0,4)，最短距離就是(|5-0|+|0-4|+1)/2=5

加1保證向上取整。

本題就是求最小生成樹的最大邊。

距離不是嚴格的曼哈頓距離，應該是

dis[i,j]=(max(x[i]-x[j],x[j]-x[i])+max(y[i]-y[j],y[j]-y[i])-1)/2+1;

可以最小生成樹，但是題目可以看出是最小生成樹的最大邊，所以二分答案應該也可以做，但是二分答案不好調，所以放最小生成樹代碼。。。

 1 #include<cstdio>
 2
 
 #include<iostream>
 3 #include<vector>
 4 #include<algorithm>
 5 #define mysister
 6 using namespace std;
 7 const int maxn=50;
 8 struct bian
 9 {
10     int u,v,w;
11     bian(int a,int b,int c):u(a),v(b),w(c){}
12     bool operator < (bian b)
13     {
14         return w<b.w;
 
15     }
16 };
17 int n,x[maxn],y[maxn],ans=0,fa[maxn];
18 vector<bian>g;
19 int find(int u)
20 {
21     return fa[u]==u?u:fa[u]=find(fa[u]);
22 }
23 int main()
24 {
25     scanf("%d",&n);
26     for(int i=0;i<n;i++)
27     {
28       scanf("%d%d",&x[i],&y[i]);
29       fa[i]=i;
30       for(int j=0;j<i;j++)
31         g.push_back(bian(i,j,(max(x[i]-x[j],x[j]-x[i])+max(y[i]-y[j],y[j]-y[i])-1)/2+1));
32     }
33     sort(g.begin(),g.end());
34     for(int i=0;i<g.size();i++)
35       if(find(g[i].u)!=find(g[i].v))
36       {
37           fa[find(g[i].u)]=find(g[i].v);
38           ans=max(ans,g[i].w);
39       }
40     printf("%d",ans);
41 }

P1661 擴散