卡爾曼濾波五個公式各個引數的意義
系統的狀態方程為：
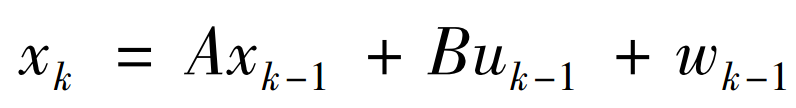
這個狀態方程是根據上一時刻的狀態和控制變數來推測此刻的狀態，wk-1是服從高斯分佈的噪聲，是預測過程的噪聲，wk-1~N(0,Q),Q即下文的過程激勵噪聲Q.
觀測方程為：
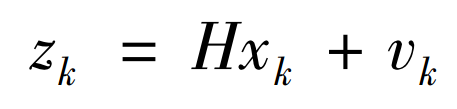
vk是觀測的噪聲，服從高斯分佈，vk~N(0,R),R即下文的測量噪聲R。
卡爾曼濾波演算法有兩個基本假設: ( 1) 資訊過程的足夠精確的模型，是由白噪聲所激發的線性( 也可以是時變的) 動態系統; ( 2) 每次的測量訊號都包含著附加的白噪聲分量 。當滿足以上假設時，可以應用卡爾曼濾波演算法。
卡爾曼濾波演算法分為兩步:預測和更新
預測：根據上一時刻( k － 1 時刻) 的後驗估計值來估計當前時刻( k 時刻) 的狀態，得到 k 時刻的先驗估計值;
更新：使用當前時刻的測量值來更正預測階段估計值，得到當前時刻的後驗估計值。
卡爾曼濾波器可以分為時間更新方程和測量更新方程。時間更新方程（即預測階段）根據前一時刻的狀態估計值推算當前時刻的狀態變數先驗估計值和誤差協方差先驗估計值; 測量更新方程（即更新階段）負責將先驗估計和新的測量變數結合起來構造改進的後驗估計。時間更新方程和測量更新方程也被稱為預測方程和校正方程。因此卡爾曼演算法是一個遞迴的預測—校正方法。
五大公式：
下面來一個個詳細剖析每個引數：
1，
: 分別表示 k － 1 時刻和 k 時刻的後驗狀態估計值，是濾波的結果之一，即更新後的結果，也叫最優估計（估計的狀態，根據理論，我們不可能知道每時刻狀態的確切結果所以叫估計）。
2，
: k 時刻的先驗狀態估計值，是濾波的中間計算結果，即根據上一時刻（k-1時刻）的最優估計預測的k時刻的結果，是預測方程的結果。
3，
：分別表示 k － 1 時刻和 k 時刻的後驗估計協方差（即的協方差，表示狀態的不確定度），是濾波的結果之一。
4，
：k 時刻的先驗估計協方差（的協方差），是濾波的中間計算結果。
5，
：是狀態變數到測量（觀測）的轉換矩陣，它負責將 m 維的測量值轉換到 n 維，使之符合狀態變數的數學形式，是濾波的前提條件之一。
6，
：測量值（觀測值），是濾波的輸入。
7，
：濾波增益陣，是濾波的中間計算結果，即大名鼎鼎的卡爾曼增益。
8，
：狀態轉移矩陣，實際上是對目標狀態轉換的一種猜想模型。例如在機動目標跟蹤中， 狀態轉移矩陣常常用來對目標的運動建模，其模型可能為勻速直線運動或者勻加速運動。當狀態轉移矩陣不符合目標的狀態轉換模型時，濾波會很快發散。
9，Q：過程激勵噪聲協方差（系統過程的協方差）。該引數被用來表示狀態轉換矩陣與實際過程之間的誤差。因為我們無法直接觀測到過程訊號， 所以 Q 的取值是很難確定的。是卡爾曼濾波器用於估計離散時間過程的狀態變數
10：R: 測量噪聲協方差。濾波器實際實現時，測量噪聲協方差 R一般可以觀測得到，是濾波器的已知條件。
11，B：是將輸入轉換為狀態的矩陣