leetcode 57. Insert Interval
link
Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).
You may assume that the intervals were initially sorted according to their start times.
Example 1:
Given intervals [1,3],[6,9], insert and merge [2,5] in as [1,5],[6,9].
Example 2:
Given [1,2],[3,5],[6,7],[8,10],[12,16]
[4,9] in as [1,2],[3,10],[12,16].
This is because the new interval [4,9] overlaps with [3,5],[6,7],[8,10].
題意:
給幾段不相交的區間,順序按左端點排序。
插入一個新的區間。這段區間的插入可能會使其中一些區間變得連續。
輸出新的不相交的區間。
表達無能,example 非常明白。
思路:
確定新區間的位置。
首先二分尋找出最大的i,滿足intervals[i].end < newInterval.start。於此i+1(若存在)有三種可能,如下圖
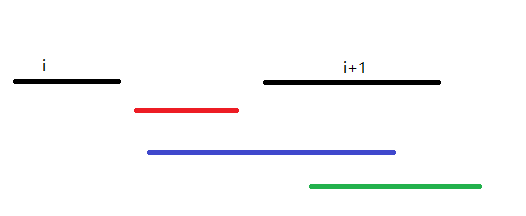
一種紅色的,newInterval和i+1不相交, 則新區間左端點為newInterval.start
一種藍色的,newInterval和i+1相交,新的區間的左端點為newInterval.start
一種綠色的,newInterval和i+1相交,新的區間的左端點為intervals[i+1].start
因此可以看出,新的區間的左端點為min(newInterval.start, intervals[i+1].start)
同理二分找出最小的i滿足intervals[i].start > newInterval.end.i-1為要處理的區間。 更新出新區間的右端點。
要處理的特例是沒有i+1/i-1的情況,其實也就是newInterval和後面/前面不相交的時候,因此更新為newInterval的信息即可。
接下來所有和newInterval有重疊的區間都不用push進最後的結果,因為他們會被作為一個新的區間的整體被放入。我們只用push進不相交的部分。也即
intervals[i].end < left_side ,
intervals[i].start > right_side
這兩個部分。
當第一次要加入
intervals[i].start > right_side
之前,我們要把新區間放進去。
註意:用in來保證新區間被push了。存在新區間在所有老區間的後方的情況,此時
intervals[i].start > right_side 不會被滿足。要在最後特判放入
代碼:
class Solution { public: int find_left(vector<Interval>& intervals, Interval newInterval){ int l = 0, r = intervals.size() - 1; int ans = -1; while(l <= r){ int mid = (l + r) >> 1; if(intervals[mid].end < newInterval.start){ ans = mid; l = mid + 1; }else{ r = mid - 1; } } return ans; } int find_right(vector<Interval>& intervals, Interval newInterval){ int l = 0, r = intervals.size() - 1; int ans = intervals.size(); while(l <= r){ int mid = (l + r) >> 1; if(intervals[mid].start > newInterval.end){ ans = mid; r = mid - 1; }else{ l = mid + 1; } } return ans; } vector<Interval> insert(vector<Interval>& intervals, Interval newInterval) { vector<Interval> ans; if(intervals.size() == 0) { ans.push_back(newInterval); return ans; } // 尋找最大的i滿足intervals[i].end < newInterval.start int front = find_left(intervals, newInterval); int left_side; if(front == intervals.size() - 1 ){ //|| front == -1){ left_side = newInterval.start; }else{ left_side = min(intervals[front + 1].start, newInterval.start); } // 尋找最小的i滿足intervals[i].start > newInterval.end int tail = find_right(intervals, newInterval); int right_side; if(tail == 0 ){//|| tail == intervals.size()){ right_side =newInterval.end; }else{ right_side = max(newInterval.end, intervals[tail-1].end); } // 以上憑此判定新區間的左右端點。 // 遍歷所有區間。若其在新區間左邊,則push, 否則在第一次在新區間的右邊的時候push新區間 bool in = false; for(int i = 0; i < intervals.size(); i++){ if(intervals[i].end < left_side) ans.push_back(intervals[i]); else if(intervals[i].start > right_side){ if(!in){ in = true; ans.push_back(Interval(left_side, right_side)); } ans.push_back(intervals[i]); } } if(!in) ans.push_back(Interval(left_side, right_side)); // 註意,若新區間沒有被push過,則要push一次 return ans; } };
leetcode 57. Insert Interval
