湖南集訓day6
阿新 • • 發佈:2017-10-11
中間 truct clas car har std -i ace esp
難度:☆☆☆☆☆☆☆☆



/* 對於第一問:f[i][j]表示前i個數,當前黑板上的數為j的概率 當前有三種情況 1.當前數不是j的倍數—>黑板上的數字改變。 2.當前數是j的倍數且當前數在前i個數中(已經選過) 3.當前數是j的倍數且沒有選過 轉移:f[i+1][j]=((j的倍數個數-i)*f[i][j]+f[i][gcd(j,k)]) 的平均值 j的倍數個數-i是沒選過的j的倍數。 對於第二問,考慮博弈論中sg函數。可知sg[i][1]二維含義同f數組)必定為0(最後黑板上剩下1必敗) sg[n][i]=0(選完了必敗) 同樣枚舉上述三種情況,取後續狀態mex值即可。*/ #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define eps 1e-8 #define N 1000 using namespace std; inline int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } int sg[N + 5][N + 5], g[N + 5][N + 5], f[N + 5], n, a[N + 5];double dp[N + 5][N + 5], ans = 0; bool getsg(int x, int y) { if (x == 1) return 1; if (sg[x][y] != -1) return sg[x][y]; bool flag = 1; if (f[x] > y) flag &= getsg(x, y + 1); for (int i = 1; i <= n; i++) if (g[x][i] != x) flag &= getsg(g[x][i], y + 1); sg[x][y] = !flag; return sg[x][y]; } int main() { freopen("cards.in", "r", stdin); freopen("cards.out", "w", stdout); scanf("%d", &n); int mx = 0; for (int i = 1; i <= n; i++) { scanf("%d", a + i); mx = max(mx, a[i]); g[0][i] = a[i]; } for (int i = 1; i <= mx; i++) for (int j = 1; j <= n; j++) f[i] += (a[j] % i == 0), g[i][j] = gcd(i, a[j]); dp[0][0] = 1; for (int i = 1; i <= n; i++) for (int j = 0; j <= mx; j++) if (dp[i - 1][j] > eps) { dp[i][j] += dp[i - 1][j] * (f[j] - i + 1) / (n - i + 1); for (int k = 1; k <= n; k++) if (g[j][k] != j) { if (g[j][k] != 1) dp[i][g[j][k]] += dp[i - 1][j] / (n - i + 1); else ans += (i + 1 & 1) * dp[i - 1][j] / (n - i + 1); } } if (n & 1) for (int j = 0; j <= mx; j++) ans += dp[n][j]; printf("%.9lf ", ans); memset(sg, -1, sizeof(sg)); if (getsg(0, 0)) puts("1.000000000"); else puts("0.000000000"); return 0; }



/* 對於60~80分,可以n^2暴力,斷掉每條邊時,O(N)求每個部分的直徑,然後相乘。 正解:倒序加邊,考慮兩棵樹合並的時候新直徑一定是原來兩個直徑四個斷點任意兩個的路徑。 所以可以首先求LCA倍增處理兩點間路徑,然後求最大。更新答案要用逆元。 */ #include<iostream> #include<cstdio> #include<cstring> #define N 100007 #define mod 1000000007 #define ll long long using namespace std; int a[N],dep[N],sum[N],fa[N][20],head[N],del[N]; int D[N][2],ans[N],f[N],len[N],end[2]; int n,m,pre,cnt; struct edge{ int u,v,net; }e[N<<1]; inline int read() { int x=0,f=1;char c=getchar(); while(c>‘9‘||c<‘0‘){if(c==‘-‘)f=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();} return x*f; } inline void add(int u,int v) { e[++cnt].u=u;e[cnt].v=v;e[cnt].net=head[u];head[u]=cnt; } void dfs(int u,int from) { fa[u][0]=from;dep[u]=dep[from]+1; sum[u]=sum[from]+a[u]; for(int i=1;i<=19;i++) fa[u][i]=fa[fa[u][i-1]][i-1]; for(int i=head[u];i;i=e[i].net) { int v=e[i].v; if(v!=from)dfs(v,u); }return; } int find(int x) { return x==f[x]?x:f[x]=find(f[x]); } int ksm(int a,int b) { int res=1; while(b) { if(b&1) res=1ll*res*a%mod; b>>=1;a=1ll*a*a%mod; }return res%mod; } int lca(int u,int v) { if(dep[u]<dep[v]) swap(u,v); int t=dep[u]-dep[v]; for(int i=0;i<20;i++) if(t&(1<<i)) u=fa[u][i]; if(u==v) return u; for(int i=19;i>=0;i--) { if(fa[u][i]!=fa[v][i]) { u=fa[u][i]; v=fa[v][i]; } }return fa[u][0]; } int getlen(int u,int v) { int L=lca(u,v); return sum[u]+sum[v]-2*sum[L]+a[L]; } int main() { freopen("forest.in","r",stdin); freopen("forest.out","w",stdout); int x,y; n=read();pre=1; for(int i=1;i<=n;i++) { a[i]=read();f[i]=i; pre=(ll)pre*a[i]%mod; D[i][0]=D[i][1]=i;len[i]=a[i]; } for(int i=1;i<n;i++) { x=read();y=read(); add(x,y);add(y,x); } dfs(1,0);int t=n;ans[n]=pre; for(int i=1;i<n;i++) del[i]=read(); for(int i=n-1;i;i--) { int id=del[i],u=e[id*2-1].u,v=e[id*2-1].v; u=find(u);v=find(v); if(len[u]<len[v]) swap(u,v); int tmax=len[u]; for(int j=0;j<2;j++) end[j]=D[u][j]; for(int j=0;j<2;j++) for(int k=0;k<2;k++) { int l=getlen(D[u][j],D[v][k]); if(l>tmax) { tmax=l; end[0]=D[u][j];end[1]=D[v][k]; } } pre=(ll) pre*ksm(len[u],mod-2)%mod; pre=(ll) pre*ksm(len[v],mod-2)%mod; f[v]=u;len[u]=tmax; for(int j=0;j<2;j++) D[u][j]=end[j]; pre=(ll) pre*len[u]%mod; ans[--t]=pre; } for(int i=1;i<=n;i++) printf("%d\n",ans[i]); return 0; }


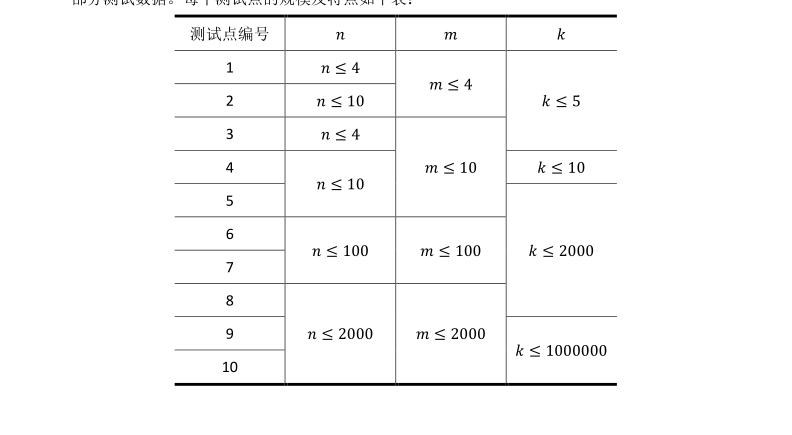
/* 這題確實是惡心,並且貌似沒有部分分...... 讓我們來瞻仰一下std做法 考慮兩列的情況。若兩列顏色分別為A,B,則A獨有的顏色就是A—A∩B ,B同理。 若是多列那還是設兩邊兩列為A,B,中間多列為C,那根據題目結論可以知道C一定是A∩B的子集。枚舉A中獨有顏色個數,B中獨有顏色個數與A中相同。若有j獨有,i共有C(K,i)*C(k-i+1,j)*C(k-i-j,j) 因為每次選擇都必須是恰好那些顏色,不能少,所以用總方案數減去不是恰好的就可以了。 */ # include<iostream> # include<cstdio> # include<cstring> # include<cstdlib> using namespace std; const int pp=1000000007; int c[2008][2008],f[2008],p[2008],ni[2008]; int n,m,k,nn; inline int power(int x,int n) { int ans=1,tmp=x; while (n) { if (n&1) ans=(long long)ans*tmp%pp; tmp=(long long)tmp*tmp%pp;n>>=1; } return ans; } void Count_c() { for (int i=0;i<=nn;i++) c[i][0]=1; for (int i=1;i<=nn;i++) for (int j=1;j<=i;j++) { c[i][j]=c[i-1][j-1]+c[i-1][j]; if (c[i][j]>=pp) c[i][j]-=pp; } } void Count_p() { int mm=(m-2)*n; for (int i=0;i<=nn;i++) p[i]=power(i,mm); } void Count_f() { f[0]=0;f[1]=1; for (int i=2;i<=nn;i++) { f[i]=power(i,n); for (int j=1;j<i;j++) { f[i]-=(long long)f[j]*c[i][j]%pp; if (f[i]<=-pp) f[i]+=pp; } if (f[i]<0) f[i]+=pp; } } void Count_ni() { ni[1]=1; for (int i=2;i<=nn;i++) ni[i]=power(i,pp-2); } int main() { freopen("photo.in","r",stdin); freopen("photo.out","w",stdout); scanf("%d%d%d",&n,&m,&k); nn=min(n,k); if (m==1) printf("%d\n",power(k,n)); else { Count_c();Count_p(); Count_f();Count_ni(); long long tmp=1,tmp1=1,sum=0,sum1; for (int s=1;s<=nn;s++) { tmp=tmp*ni[s]%pp; tmp=tmp*(k-s+1)%pp; tmp1=1;sum1=0; for (int j=0;j<=s;j++) { sum1+=tmp1*c[s][s-j]%pp*p[s-j]%pp; if (sum1>=pp) sum1-=pp; tmp1=tmp1*ni[j+1]%pp; if (k-s<j+1) break; tmp1=tmp1*(k-s-j)%pp; } sum+=tmp*f[s]%pp*f[s]%pp*sum1%pp; if (sum>=pp) sum-=pp; } printf("%d\n",sum); } fclose(stdin); fclose(stdout); return 0; }
湖南集訓day6
