沈陽集訓day6

阿新 • • 發佈：2018-07-07

upload ron print max 規則 != 問題：題解會有

問題 A: YY的矩陣

題目描述

YY有一個大矩陣（N*M）, 矩陣的每個格子裏都有一個整數權值W[i,j]（1<=i<=M,1<=j<=N）對於這個矩陣YY會有P次詢問，每次詢問這個大矩陣的一個子矩陣內的最大值。

輸入

第一行兩個整數N和M。接下來N行，每行M個整數然後，一行是整數P；接下來P行，每行4個整數r1, c1, r2, c2（分別表示子矩陣的左上角坐標和右下角坐標）

輸出

共P行，每行一個整數，表示相應的最大值。

樣例輸入

樣例輸出

提示

數據範圍：

60%的數據：N×M×P<10^8

100%的數據：1 <= N, M <= 300；1 <= P <= 1,000,000；1 <= r1 <= r2 <= N, 1 <= c1 <= c2 <= M，1<=W[i][j]<=10000.

題解：二維ST表，O(1)查詢，log要開成N那麽大

#include <bits/stdc++.h>
 
using namespace std;
int n, m, a[305][305][10][10], lo[310];
void init(){
     
for(int pi = 0; pi < 10; pi++)
        for(int pj = 0; pj < 10; pj++)
            if(!pi && !pj)continue;
            else for(int i = 1; i + (1<<pi) -1 <= n; i++)
                for(int j = 1; j + (1<<pj) -1 <= m; j++){
                    if(!pi)
                        a[i][j][pi][pj]  
= max(a[i][j][pi][pj - 1], a[i][j + (1<<(pj-1))][pi][pj - 1]);
                    else
                        a[i][j][pi][pj] = max(a[i][j][pi - 1][pj], a[i + (1<<(pi-1))][j][pi - 1][pj]);
                   // printf("%d %d %d %d %d\n", i,j,pi,pj,a[i][j][pi][pj]);
                }
 
}
int query(int x1, int y1, int x2, int y2){
    int pi = lo[x2 - x1 + 1], pj = lo[y2 - y1 + 1];
    int ans1 = max(a[x1][y1][pi][pj], a[x2 - (1<<pi) +1][y1][pi][pj]);
    int ans2 = max(a[x1][y2 - (1<<pj) + 1][pi][pj], a[x2 - (1<<pi) + 1][y2 - (1<<pj) + 1][pi][pj]);
    return max(ans1 ,ans2);
 
}
 
int main()
{
    scanf("%d%d", &n,  &m);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            scanf("%d", &a[i][j][0][0]);
    lo[0] = -1;
    for(int i = 1; i <= 305; i++)lo[i] = lo[i/2] + 1;
    init();
    int q;
    scanf("%d", &q);
    while(q--){
        int x1, x2, y1, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        int ans = query(x1, y1, x2, y2);
        printf("%d\n", ans);
    }
    return 0;
}

View Code

問題 B: WYT的刷子（一道單調隊列的好題）

題目描述

WYT有一把巨大的刷子，刷子的寬度為M米，現在WYT要使用這把大刷子去粉刷有N列的柵欄（每列寬度都為1米；每列的高度單位也為米，由輸入數據給出）。使用刷子的規則是： 1、與地面垂直，從柵欄的底部向上刷 2、每次刷的寬度為M米（當剩余柵欄寬度不夠M米的話，刷子也可以使用，具體看樣例2） 3、 對於連續的M列柵欄，刷子從底向上，刷到的高度只能到這M列柵欄的最低高度。 WYT請你回答兩個問題： 1、最少有多少個單位面積不能刷到（單位面積為1平米） 2、在滿足第一問的條件下，最少刷幾次？

輸入

共兩行：第一行兩個整數N和M。第二行共N個整數，表示N列柵欄的高度

輸出

兩行，每行一個整數，分別為最少剩余的單位面積數量和最少刷的次數。

樣例輸入

Input1:
5 3
5 3 4 4 5
Input2:
10 3
3 3 3 3 3 3 3 3 3 3
Input3:
7 4
1 2 3 4 3 2 1

樣例輸出

Output1:
3
2
Output2:
0
4
Output3:
4
4

提示

樣例1的解釋：

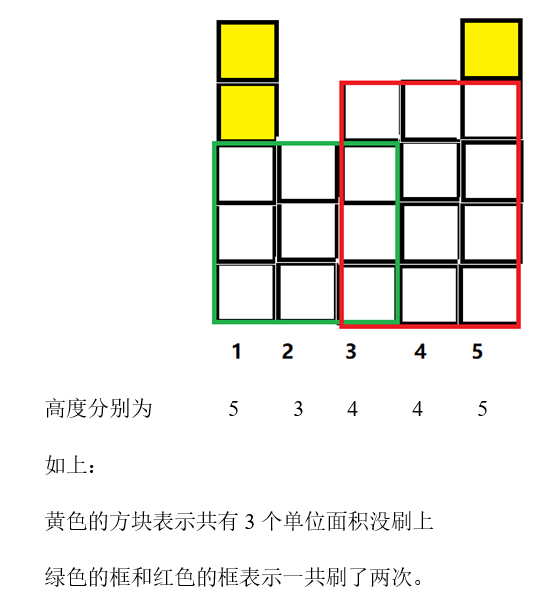
技術分享圖片

數據範圍：

30%的數據：N<=10^3

50%的數據：N<=10^5

100%的數據：1<=N<=10^6, 1<=M<=10^6,N>=M, 每列柵欄的高度<=10^6.

題解：兩個單調隊列，一個維護區間內最小值，一個在區間內維護最大值，就可以得到可以塗的輪廓線；（自己畫圖）

遇到高度不一樣或長度不夠則要多一個刷子；

單調對列求區間最大用遞減隊列；

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int M = 1e6+10;
struct Queue{
    int id; ll h;
}q[M], q2[M], q3[M];
 
ll a[M], lim[M];
 
int main(){
    int n, m; ll ret = 0;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)scanf("%lld", &a[i]);
    int h = 1, t = 0;
    for(int i = 1; i <= n; i++){
        while(h <= t && q[t].h >= a[i])t--;
        q[++t].id = i; q[t].h = a[i];
        if(i >= m){
            if(q[h].id <= i - m)h++;
            q2[i].h = q[h].h; q2[i].id = q[h].id;
        }
    }
    for(int i = 1; i < m; i++)q2[i].id = i, q2[i].h = -1e8;
    h = 1, t = 0;
    for(int i = 1; i <= n; i++){
        while(h <= t && q3[t].h <= q2[i].h)t--;
        q3[++t].id = i; q3[t].h = q2[i].h;
        if(i >= m){
            if(q3[h].id <= i - m)h++;
            lim[i - m + 1] = q3[h].h;
            ret += a[i - m + 1] - lim[i - m + 1];
        }
    }
    ll tt = q2[n].h;
    for(int i = n; i > n - m + 1; i--){
        tt = max(tt, q2[i].h);
        lim[i] = tt;
        ret += a[i] - lim[i];
    }
    //for(int i = 1; i <= n; i++)printf("%d ", lim[i]);
    int lst = 1, cnt = 1;
    for(int i = 1; i <= n; i++){
        if(i - lst + 1 > m || lim[lst] != lim[i]){
            lst = i; cnt++;
        }
    }
    printf("%lld\n%d\n", ret, cnt);
}

View Code

問題 C: 2017種樹

題目描述

2017共有N棵樹從0到N-1標號。現要把這些樹種在一條直線上，第i棵樹的種植位置X[i]如下確定： X[0] = X[0] MOD L； X[i] = (X[i-1]*A+B) MOD L。每棵樹種植的費用，是所有標號比它小的樹與它的距離之和。2017請你計算各棵樹的費用之積，最後對1000000007取余。

輸入

共五行：第一行為N 第二行為L 第三行為X[0] 第四行為A 第五行為B

輸出

總費用

樣例輸入

樣例輸出

提示

樣例解釋：

5棵樹的位置分別為: 3, 4, 5, 6, 7.

費用分別為: 1, 3, 6, 10. （從第一棵樹開始）

總費用為： 1 × 3 × 6 × 10 = 180.

數據範圍：

10%的數據：N<=10;

60%的數據：N<=5×10^4;

100%的數據：N,L<=200000; X[0] ,A, B<=10^9.

題解：值域線段樹

一個樹與其他樹距離和：他離開頭的距離*在他前面樹的個數 - 前面樹離開頭距離總和 + 他離結尾的距離*在他後面樹的個數 - 後面樹離結尾距離總和；用值域線段樹記錄前面樹的個數距離，log（N)求一棵樹離其他樹的距離，總復雜度Nlog(N);

註意到處都要mod，還要防止減成負數，還有nd->zuo = (nd->zuo + pos) % mod; 不能直接賦值成位置，因為有多個樹，這個地方wa了很久

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int M = 200005;
const ll mod = 1000000007;
int cnt, m;
ll dis[M], tmp[M];
ll ans = 1;
struct Node{
    ll zuo, you;
    int zz;
    Node *ls, *rs;
 
    void up(){
        zuo = (ls->zuo + rs->zuo) % mod;
        you = (ls->you + rs->you) % mod;
        zz = ls->zz + rs->zz;
        //yy = ls->yy + rs->yy;
    }
}pool[M<<2], *root, *tail = pool;
Node * build(int l = 1, int r = m){
    Node * nd = ++tail;
    if(l == r)nd->zuo = nd->you = nd->zz = 0;
    else {
        int mid = (l + r) >> 1;
        nd->ls = build(l, mid);
        nd->rs = build(mid+1, r);
        nd->up();
    }
    return nd;
}
#define Ls nd->ls, l, mid
#define Rs nd->rs, mid+1, r
ll query1(int L, int R,  Node * nd = root, int l = 1, int r = m){
    if(L <= l && R >= r){
        cnt += nd->zz;
        return nd->zuo;
    }
    int mid = (l + r) >> 1;
    ll ans = 0;
    if(L <= mid) ans = query1(L, R, Ls);
    if(R > mid) ans = (ans+ query1(L, R, Rs)) % mod;
    return ans;
}
ll query2(int L, int R,  Node * nd = root, int l = 1, int r = m){
    if(L <= l && R >= r){
        cnt += nd->zz;
        return nd->you;
    }
    int mid = (l + r) >> 1;
    ll ans = 0;
    if(L <= mid) ans = query2(L, R, Ls);
    if(R > mid) ans = (ans+ query2(L, R, Rs)) % mod;
    return ans;
}
void insert(int pos, ll d2, Node * nd = root, int l = 1, int r = m){
    if(l == r){
        nd->zz ++;
        nd->zuo = dis[pos];
        nd->you = d2;
    }
    else {
        int mid = (l + r) >> 1;
        if(pos <= mid)insert(pos, d2, Ls);
        else insert(pos, d2, Rs);
        nd->up();
    }
}
int main()
{
    int n;
    ll L, A, B;
    scanf("%d%lld%lld%lld%lld", &n, &L, &dis[1], &A, &B);
    dis[1] %= L;
    tmp[1] = dis[1];
    for(int i = 2; i <= n; i++)tmp[i] = dis[i] = (dis[i-1]*A+B) % L;
   // cout<<"OO";
    sort(tmp+1, tmp+1+n);
    m = unique(tmp+1, tmp+1+n) - tmp - 1;
    root = build();
  //  cout<<"h1"<<endl;
    for(int i = 1; i <= n; i++){
        int pos = lower_bound(tmp+1, tmp+1+m, dis[i]) - tmp;
        ll here = 0;
        cnt = 0;
        ll a1 = query1(1, pos);
     //   cout<<"L";
        here = ( (1LL*cnt*dis[i] % mod - a1) + mod * 2 ) % mod;
        cnt = 0;
        ll a2 = query2(pos, m);
    //    cout<<"KK";
        ll dd = tmp[m] - dis[i];
        here = (here + ( (1LL*cnt*dd%mod - a2) % mod) + mod * 2) % mod;
        if(!here && i == 1)here = 1;
        insert(pos, dd);
        ans = (ans * here) % mod;
        //cout<<ans<<endl;
    }
    printf("%lld\n", ans);
    return 0;
}

View Code

沈陽集訓day6

upload ron print max 規則 != 問題：題解會有問題 A: YY的矩陣題目描述 YY有一個大矩陣（N*M）, 矩陣的每個格子裏都有一個整數權值W[i,j]（1<=i<=M,1<=j<=N）對於這個矩陣YY會有P次詢

沈陽集訓day6

問題 A: YY的矩陣

題目描述

輸入

輸出

樣例輸入

樣例輸出

提示

問題 B: WYT的刷子（一道單調隊列的好題）

題目描述

輸入

輸出

樣例輸入

樣例輸出

提示

問題 C: 2017種樹

題目描述

輸入

輸出

樣例輸入

樣例輸出

提示

相關推薦